Гибкость макромолекулы
Макромолекулы практически никогда не находятся в предельно вытянутом положении, они стремятся каким-либо образом свернуться, чтобы принять более выгодное состояние (проявляется стремление принять положение, отвечающее минимуму энергии).
Контурной длиной цепи называется длина максимально вытянутой цепи, однако из-за малой вероятности такой конформации она не является главным фактором, определяющим свойства данного полимера.
Рассмотрим факторы, определяющие конформации реальных молекул на примере молекулы 1,2-дизамещенных производных этана (1,2-дихлорэтана).
За 1 секунду эта молекула претерпит 1012 конформационных переходов под действием вращения вокруг связи С–С одной группы –CH2Cl относительно другой.
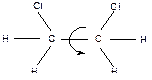 или в проекции
или в проекции 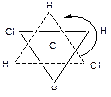
На рисунке 16.1. приведена зависимость энергии Е от угла вращения φ. В случае макромолекулы полиэтилена зависимости будут аналогичны, но атомы Cl заменены –СН2- группами цепи. Минимумы соответствуют транс- и гош-конформации, максимумы – цис-конформации. Если энергия теплового движения kT превышает возможную энергию, которую может принять молекула, образуя цис-конформации, то происходит вращение вокруг связи С–С и молекула может принимать цис-, транс-, или гош-конформацию (промежуточную конформацию).
В этом случае зависимость энергии от угла вращения будет следующей:
|
|
|
|
|
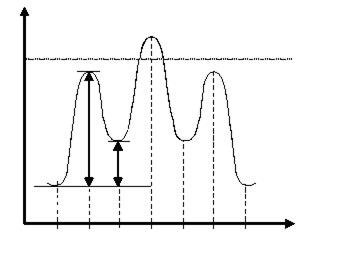
0 60 120 180 240 300 360
Рис. 16.1. Зависимость энергии Е от угла вращения φ
Цис-конформация часто бывает недоступной, т. к. энергия теплового движения может быть меньше, чем энергия, необходимая для перевода молекулы в это положение.
Возможна некоторая промежуточная выгодная конформация, называемая гош-конформацией. Транс- и гош-конформации определяют возможные изменения конформаций макромолекулы. Разность энергий транс- и гош-конформаций представляют собой термодинамическую гибкость макромолекулы (ΔU˝). Разность энергий ΔU΄ представляет собой кинетическую гибкость, определяемая как энергия активации перехода от транс- к гош-конформации. Кинетическая и термодинамическая гибкости макромолекулы являются характеристиками гибкости цепи макромолекулы.
Модели макромолекул
1. Модель свободно сочлененной цепи (модель ССЦ)
Эта модель является наиболее идеализированным представлением о макромолекуле.
Положения, позволяющие построить данное представление:
а) может происходить относительно свободное вращение звеньев друг относительно друга;
б) взаимодействия между заместителями в макромолекуле отсутствуют;
в) валентный угол не фиксирован;
г) расстояние между атомами строго фиксировано;
д) объемами атомов углерода пренебрегают.

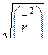
Рис. 16.2. Модель свободно сочлененной цепи (ССЦ)
Удобной статистической характеристикой конформации цепи является 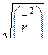 - среднее квадратичное расстояние между концами цепи. Математическое рассмотрение этой модели приводит к следующему выражению:
- среднее квадратичное расстояние между концами цепи. Математическое рассмотрение этой модели приводит к следующему выражению:
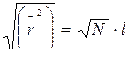 , (16.1)
, (16.1)
где N – число звеньев в цепи, а l – длина одного звена
Полная длина цепи представляет собой произведение этих величин:
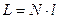 (16.2)
(16.2)
Макромолекулу можно характеризовать степенью свернутости:
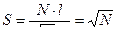 (16.3)
(16.3)
Степень свернутости представляет собой потенциальную возможность изменения размеров макромолекулы.
Количество звеньев эквивалентно степени полимеризации, поэтому при увеличении степени полимеризации возможность изменения размеров увеличивается.
Пример: при степени полимеризации 102 макромолекула может изменять свой размер в 10 раз, при 104 – в 100 раз.
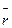 соответствует наиболее вероятному значению r, т.е. среднему значению
соответствует наиболее вероятному значению r, т.е. среднему значению
Распределение макромолекул по значениям расстояний между концами цепи является гауссовым:
 W(r)
W(r)
rmax r
Рис. 16.3. Распределение макромолекул по значениям расстояний между концами цепи
поэтому клубок, образуемый макромолекулой, часто называют гауссовым клубком.
2. Модель с фиксированным валентным углом
Модель представляется в следующем виде:

2 θ
α
1 3
Рис. 16.4. Модель с фиксированным валентным углом
вращение происходит свободно, но только по образующим конуса.
Средне-квадратичное расстояние равно в этом случае:
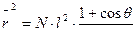 (16.4)
(16.4)
Для α = 109,5◦ в полиэтилене θ = 180◦ - α = 71◦, cosθ = 1/3 и 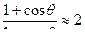 , поэтому можно заключить, что по сравнению с предыдущей моделью клубок немного разбухает (в ~ 1,4 раза), жесткость молекулы увеличивается, но зависимость
, поэтому можно заключить, что по сравнению с предыдущей моделью клубок немного разбухает (в ~ 1,4 раза), жесткость молекулы увеличивается, но зависимость
|
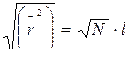 (16.5)
(16.5)
сохраняется.
3. Модель с заторможенным вращением
Эта модель аналогична предыдущей модели, вводится лишь положение о том, что происходит заторможенное вращение, некоторые конформации недоступны из-за того, что энергии теплового движения недостаточно для их реализации.
Поэтому вводится поправка, учитывающая углы заторможенного вращения, при которых реализуются возможные конформации:
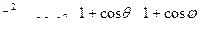 (16.6)
(16.6)
Наконец, переход к поворотно-изомерной модели, учитывающей не только фиксированные транс- и гош-конформации соседних звеньев, но и различия в энергиях между ними, также не приводит к нарушению зависимости 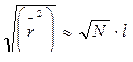 , а лишь влияет на величину коэффициента пропорциональности, который будет зависеть от разности энергий транс- и гош-конформаций.
, а лишь влияет на величину коэффициента пропорциональности, который будет зависеть от разности энергий транс- и гош-конформаций.
Таким образом, переходим от идеализированной модели к более реальной модели.
Рассмотрим участок цепи:

2 4
1 3
Рис. 16.5. Модель с заторможенным вращением
Здесь еще сохраняется корреляция положения атома 1 относительно атома 4.
Существует некоторый атом n на, котором корреляция теряется, т. е. можно считать, что он движется независимо от атома 1. Участки, состоящие из n атомов, в которых атом n начинает перемещаться независимо от атома m, называются сегментами (сегментами Куна). Таким образом, макромолекулу можно условно разделить на сегменты, перемещающиеся независимо друг относительно друга.
Исходя из этого, можно применить модель свободно-сочлененной цепи для любой реальной цепи, заменяя величину сегмента Куна, равную длине химической связи в модели ССЦ на больший отрезок цепи, соответствующий реальному сегменту Куна для данного полимера.
Независимо от способов разбивки на участки контурная длина цепи L не изменяется (она определяется лишь числом мономерных остатков, образующих макромолекулу).

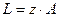
 (16.7)
(16.7)
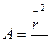 , z – число сегментов, А – длина сегмента, L – контурная длина цепи
, z – число сегментов, А – длина сегмента, L – контурная длина цепи
Величина  определяется методом светорассеяния.
определяется методом светорассеяния.
На основании экспериментальных данных можно составить следующую таблицу:
Таблица 16.1.
Величины длины звена и числа мономерных звеньев в сегменте
| Полимер | Длина звена А, А˚ | Число мономерных звеньев в сегменте |
| Полидиметилсилоксан | 14 | 4,9 |
| Полипропилен | 21,7 | 8,6 |
| Полистирол | 20 | 7,9 |
| Поливинилхлорид | 29,6 | 11,7 |
| Тринитроцеллюлоза | 200 | 30 |
Гибкость – способность макромолекулы изменять свою форму под действием теплового движения.
Гибкость макромолекулы связана с величиной сегмента: чем меньше величина сегмента, тем больше гибкость молекулы.
Таким образом, длина сегмента Куна является важной характеристикой макромолекулы.
Наглядное представление о конформации реальных макромолекул различной длины можно получить, построив с помощью компьютера их траектории в пространстве. Так для воображаемой цепи полиэтилена ее конформация (траектория) строится путем последовательного размещения каждого последующего звена с учетом длины связи С–С, угла поворота относительно транс-конформации (φ = 0) в гош-конформации (± 115◦С) и разности энергий транс- и гош-конформаций.
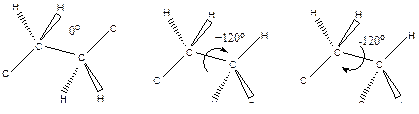
Результаты математического эксперимента представлены в таблице 16.2. для трех длин цепей 50, 500 и 3000 связей.
Таблица 16.2.
Результаты математического эксперимента для цепей полиэтилена различной длины
| n | Vгл/Vклуб | 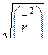 /Lтранс /Lтранс
|
| 50 | 0,1 | 0,25 |
| 500 | 0,03 | 0,12 |
| 3000 | 0,01 | 0,02 |
где Vгл и Vклуб – объемы молекулы в конформации плотных глобул и занимаемый объем в рассчитанной конформации, а Lтранс и 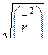 - расстояние между концами цепи в конформациях транс-зигзага и рассчитанной траекторией цепи. Видно, что конформации линейных макромолекул очень «рыхлые», фрагментами молекулы заполнена лишь небольшая часть пространства, в котором она находится, и плотность заполнения пространства уменьшается с ростом молекулярной массы, а расстояние между концами цепи оказывается значительно меньше длины полностью вытянутой цепи в соответствии с предсказаниями теории.
- расстояние между концами цепи в конформациях транс-зигзага и рассчитанной траекторией цепи. Видно, что конформации линейных макромолекул очень «рыхлые», фрагментами молекулы заполнена лишь небольшая часть пространства, в котором она находится, и плотность заполнения пространства уменьшается с ростом молекулярной массы, а расстояние между концами цепи оказывается значительно меньше длины полностью вытянутой цепи в соответствии с предсказаниями теории.
Физико-механические свойства полимеров
Полимерным материалам свойственны следующие свойства:
1) Способность деформироваться значительно и обратимо;
2) Как высокие, так и низкие модули упругости;
3) Анизотропия свойств;
4) Зависимость свойств полимеров от времени;
5) Растворы полимеров обладают аномально высокой вязкостью, существенно отличающейся от вязкости растворов мономеров.
3 основных свойства макромолекул:
· Цепное линейное строение
· Высокая ММ
· Слабые взаимодействия между макромолекулами
Характеристики макромолекул:
1. Молекулярная масса и длина макромолекул
2. Конфигурация (определяет строение макромолекул). Существует 3 вида изомерии: локальная, оптическая и цис-транс изомерия
3. Конформация (определяет форму макромолекул)
Конформация – это пространственное расположение атомов и групп атомов, которое создается набором и последовательностью конфигураций, их взаимным расположением в молекуле (обусловленных тепловым движением или внешним воздействием на систему).
Вопросы для самостоятельной проработки:
1. Какими отличительными свойствами характеризуются полимерные материалы?
2. Что такое контурная длина цепи?
3. Понятие о конформационных переходах в макромолекуле.
4. Чем обусловлена гибкость макромолекул?
5. Какими моделями описывают макромолекулы?
6. Как рассчитывают среднее квадратичное расстояние?
7. Что такое сегмент полимерной цепи? Как зависит величина сегмента от строения молекул?
Задачи для самостоятельного решения
- Основные понятия и определения химии и физики полимеров
1.1. Понятия о статистическом сегменте. Модель свободно-сочлененной цепи
Вопросы 1501 – 1504, 1405 – 1408,1309 – 1311,
1.2. Гибкость и размеры макромолекулы
Вопросы 2501 – 2503,2404 – 2410, 2311 – 2314
Дата: 2019-04-23, просмотров: 489.