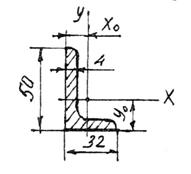
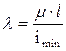Для стальной стойки, сжимаемой силой F, поперечное сечение которой составлено из двух швеллеров (рисунок 5) таким образом, что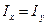 
(равноустойчивая стойка) требуется:
1. Из условия устойчивости стойки определить номер швеллера при допускаемом напряжении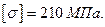 
2. Найти критическую силу и коэффициент запаса устойчивости.
3. Из условия равноустойчивости определить размер с поперечного сечения.
Исходные данные:
1. Номер схемы Nсх определяется следующим образом:
при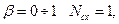 
при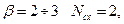 
при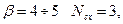 
при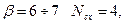 
при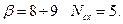 
2. 
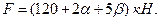
3. 
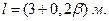
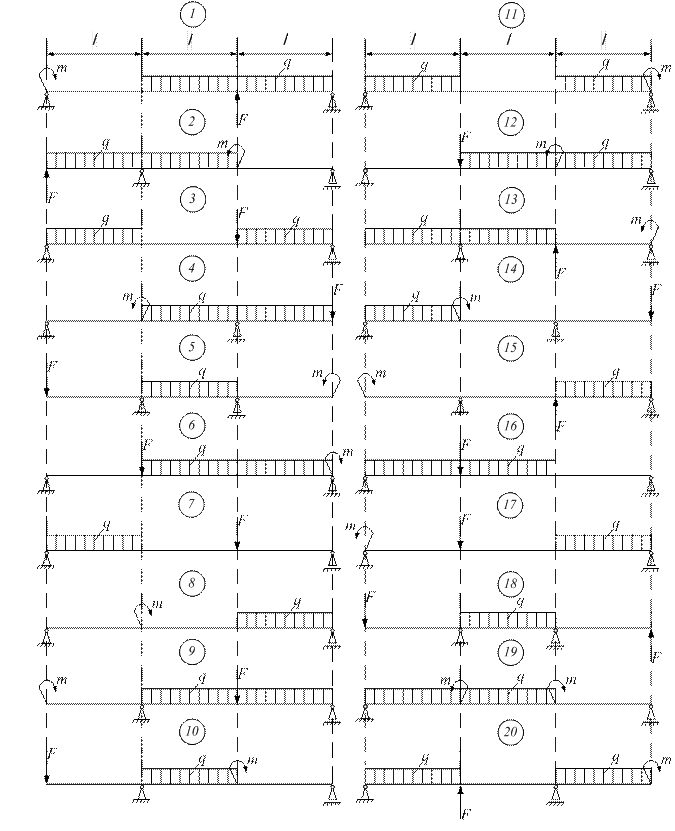
Рисунок 4 − Схемы стальных балок
  | |||||
  | |||||
  | |||||
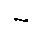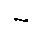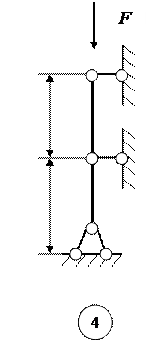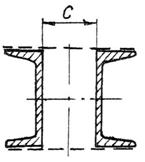
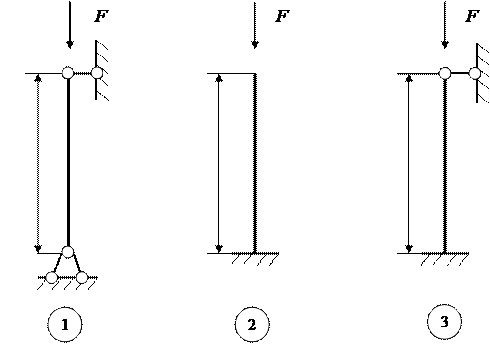
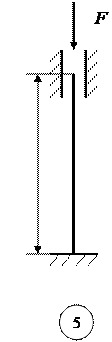
Рисунок 5 − Схемы к расчету сжатых стоек на устойчивость
ПРИМЕРЫ РЕШЕНИЯ контрольных ЗАДАЧ
Пример № 1
Для ступенчатого бруса (рисунок 6) необходимо:
1. Определить продольные силы в поперечных сечениях и построить эпюру.
2. Определить нормальные напряжения в поперечных сечениях и построить их эпюру.
3. Определить опасное сечение и указать, выдержит ли брус на прочность, если расчетное напряжение на сжатие и растяжение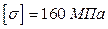 
.
4. Определить нормальные и касательные напряжения в наклонной площадке, расположенной под углом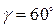 
в опасном сечении.
5. Определить перемещения сечений и построить эпюру.
Данные для расчета: F1 = 100 кН, F2 = 50 кН, F3 = 150 кН, А1 = 6 см2, А2 = 7,2 см2, А3 = 8,4 см2, l1 = 1 м, l2 = 0,6 м, l3 = 0,5 м, l4 = 0,4 м, l5 = 0,7 м, Е = 2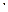 
105 МПа.
Решение
Ступенчатый брус необходимо разбить на отдельные участки. Отсчет участков производится от свободного конца для того, чтобы не определять реакцию в заделке. Границами участков являются сечения, в которых приложены внешние силы или меняется площадь. Первый участок будет между точками В и С, так как в точке С меняется площадь поперечного сечения. Брус от точки С до точки Е имеет постоянное сечение, но в точке D приложена сила F2 , поэтому от точки С до D будет второй участок, а от D до Е – третий. В точке Е меняется площадь сечения бруса, а в точке М приложена сила F3, поэтому четвертый участок – от точки Е до М, пятый – от М до Р. При определении внутренних усилий пользуются методом сечений. Продольная сила N равна сумме внешних сил, действующих на правую от рассматриваемого сечения часть бруса. Силы, растягивающие брус, являются положительными, а сжимающие – отрицательными.
Рассмотрим сечение 1-1. На правую часть бруса действует только одна сила F1, являющаяся растягивающей. Следовательно, продольная сила N1 будет положительной.
N1 = F1= 100 кH.
Рассмотрим сечение 2-2. На правую часть бруса действует только одна сила F1:
N2 = F1 = 100 кH.
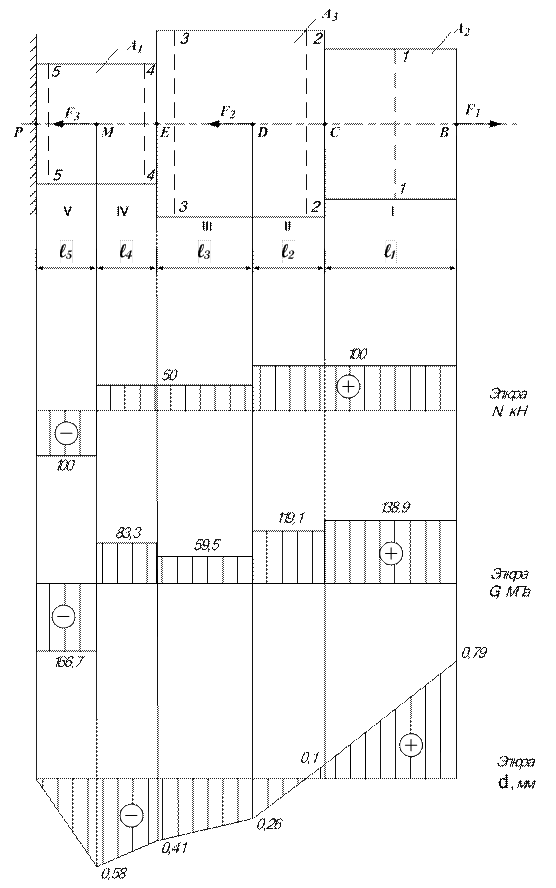
Рисунок 6 − Схема бруса и эпюры внутренних усилий
Сечение 3-3. На правую часть действуют силы F1 и F2, причем сила F2 является сжимающей, следовательно, должна браться со знаком «минус»:
N3 = F1 – F2= 100 – 50 = 50 кН.
Сечение 4-4. Действуют те же силы F1 и F2:
N4 = F1 – F2 = 50 кН.
Сечение 5-5. На правую часть действуют три силы F1, F2, F3, причем сила F3 – сжимающая:
N5 = F1 – F2 – F3= 100 – 50 – 150 = –100 кН.
Определив значения внутренних усилий на каждом участке, строим эпюру продольных сил N. Положительные значения откладываем сверху, отрицательные – снизу. Поскольку на участках продольная сила имеет постоянное значение, эпюра N будет представлять собой линии, параллельные оси бруса.
Проверим правильность построения эпюры. В точках приложения внешних сил эпюра N должна делать скачок на величину этих сил. В точке D приложена сила F2 и на эпюре продольной силы N имеется скачок на величину 50 кН, в точке М соответственно на 150 кН. Нормальные напряжения в поперечном сечении находят по формуле
s =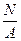 
;
на первом участке:
s I =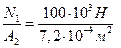 
= 138,9×106 Па =138,9 МПа;
на втором участке:
s II =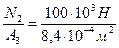 
= 119,1×106 Па =119,1 МПа;
на третьем участке:
s III =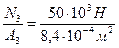 
= 59,5×106 Па =59,5 МПа;
на четвертом участке:
s IV =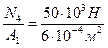 
= 83,3×106 Па =83,3 МПа;
на пятом участке:
s V =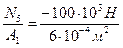 
= – 166,7×106 Па = –166,7 МПа.
Строим эпюру нормальных напряжений. Положительные значения откладываем сверху, отрицательные – снизу от оси. Так как напряжение на участке постоянно, эпюра изображается горизонтальными линиями.
Поскольку допускаемое напряжение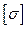 
одинаково на растяжение и сжатие, на эпюре s следует найти максимальное значение напряжения без учета знака. Опасное сечение будет на пятом участке, где smax = 166,7 МПа.
Условие прочности имеет вид:
smax ≤ [s].
В данном случае действующее на пятом участке напряжение превосходит допускаемое smax = 166,7 МПа ³ [s] = 160 МПа. Но превышение до 5% считается несущественным, и полагают, что прочность в таком случае обеспечена. Определим процент превышения:
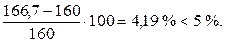
Условие прочности обеспечено.
Нормальные напряжения в наклонной площадке определяют по формуле:
s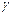 
=cos2 
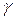= –166,7×cos260o = –41,7 МПа.
касательные:
t 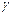=1/2s 
sin2 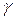= 1/2 (–166,7) sin120° = –72,2 МПа.
Величины деформаций каждого участка определяют по формуле:
Dl =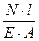 
.
первого участка:
Dl1=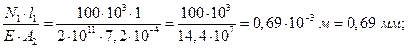 
второго участка:
Dl2=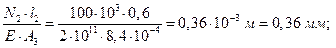 
третьего участка:
Dl3=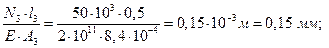 
четвертого участка:
Dl4=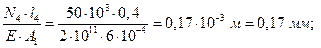 
пятого участка:
Dl5=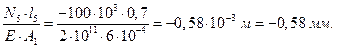 
Знак «минус» указывает на то, что пятый участок сожмется.
Строим эпюру перемещений. В сечении Р перемещения отсутствуют.
Сечение М сместится относительно Р на величину деформации V участка.
dм = Dl5 = –0,58 мм.
Сечение Е относительно М сместится на величину Dl4.
dЕ = dМ + Dl4 = –0,58 мм + 0,17 мм = –0,41 мм.
Сечение D сместится относительно Е на Dl3.
dД = dЕ + Dl3 = –0,41 мм = –0,416 + 0,143 = –0,26 мм.
Сечение С сместится относительно D на Dl2.
dС = dД + Dl2 = –0,26 + 0,36 = 0,1 мм.
Сечение В сместится относительно С на Dl1.
dВ = dС + Dl1 = 0,1 + 0,69 = 0,79 мм.
На эпюре откладываем соответствующие значения перемещений и соединяем их прямыми линиями.
Пример №2
Необходимо определить диаметр круглого стального бруса переменного сечения, заделанного с двух сторон (рисунок 7, а) из условия прочности, когда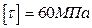 
и жесткости, когда 
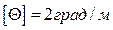, если 
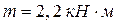. Модуль сдвига стали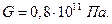 
Решение
Так как в одно уравнение равновесия (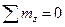 
) войдут два неизвестных – реактивные моменты в заделках, то задача является один раз статически неопределимой.
Для составления уравнения деформаций изобразим эквивалентную систему (рисунок 7, б), отбросив правую заделку и заменив ее моментом х. Уравнение деформаций выражает условие отсутствия угла поворота сечения 1. Из этого следует, что угол закручивания всего бруса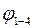 
равен нулю.
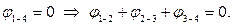
Формула для угла закручивания –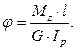 
Уравнение деформаций принимает вид:
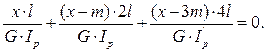
Выразим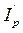 
(полярный момент инерции сечения на участке 3-4) через момент инерции 
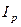участка 1-3.
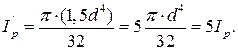
Выполним эту подстановку и решим уравнение получим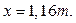 
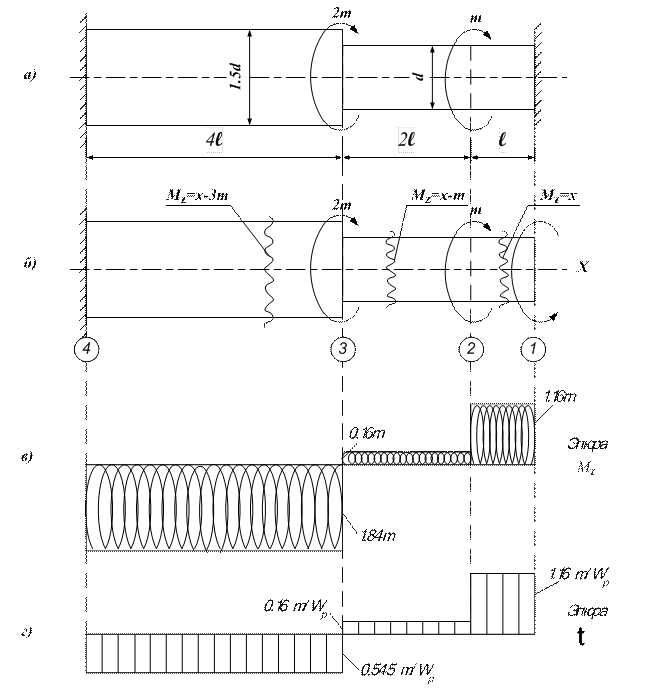
Рисунок 7 − К расчету стального бруса при кручении
Строим эпюру крутящего момента Мz (рисунок 7, в). Обратим внимание, что скачки на эпюре будут в тех сечениях, в которых приложены внешние моменты (на величину этих моментов).
Далее строим эпюру касательных напряжений, действующих в точках контура поперечных сечений (рисунок 7, г).
Участок 1-2: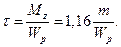 
Участок 2-3: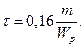 
Для определения касательных напряжений на участке 3-4 выразим момент сопротивления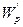 
через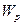 
:
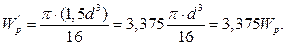
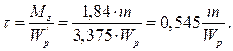
Наибольшие касательные напряжения оказались на участке 1-2. Записываем условие прочности:
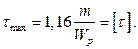
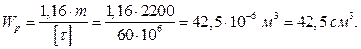
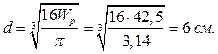
Найдем диаметр из условия жесткости. Относительный угол закручивания на участке 1-2:
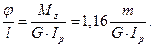
На участке 3-4:
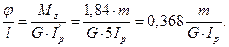
Условие жесткости:
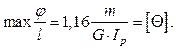
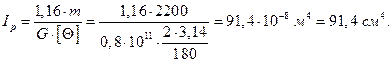
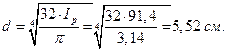
Принимаем окончательно из условия прочности d=60 мм.
Пример № 3
Для сечения (рисунок 8) необходимо найти положение главных центральных осей и вычислить главные моменты и главные радиусы инерции.
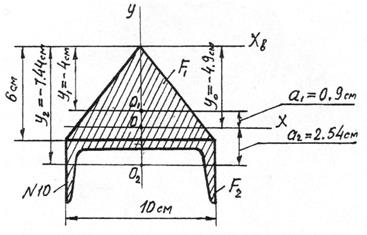
Рисунок 8 − Схема составного сечения
Из сортамента прокатных профилей выписываем данные по швеллеру №10У (ГОСТ 8240-97), изображенному на рисунке 9.
| А = 10,90 см2; Ix = 174,0 см4; Iу = 20,40 см4. |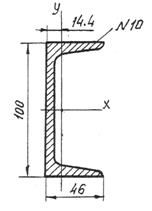 
Рисунок 9. Схема сечения швеллера
|
Решение
Через вершину треугольника проводим вспомогательную ось Хв и определяем координату Y0 центра тяжести сечения.
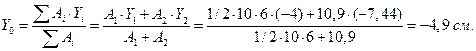
Проводим центральную ось Х и находим расстояние а1 и а2 между осью Х и параллельными ей центральными осями треугольника и швеллера.
Вычисляем главные моменты инерции сечения.
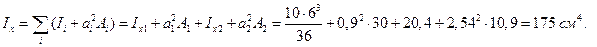
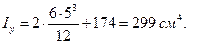
Для треугольника использованы следующие формулы (рисунок 10).
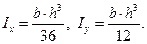
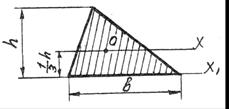
Рисунок 10 − К расчету главных моментов инерции
Вычисляем главные радиусы инерции сечения:
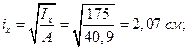
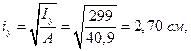
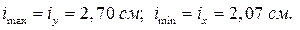
Пример № 4
Для заданной балки (рисунок 11) необходимо:
1. Построить эпюры поперечных сил и изгибающих моментов.
2. Из расчета на прочность подобрать двутавровое, круглое и прямоугольное сечение (приняв для прямоугольного сечения отношение высоты к ширине, равное двум), если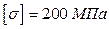 
.
Решение
Реакции опор Rв и Rд направим вверх. Составим уравнение статического равновесия.
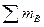= 0;
F×l – q×1,5×(1,5/2) – m + RД×2,5 = 0; RД = 11,5кН.
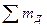= 0;
F×3,5 – RВ×2,5 + q×1,5(1,5/2 + 1 ) – m = 0; RВ = 73,5 кH.
Проверка:
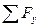= 0; – F + RВ – q×1,5 + RД = 0;
–40 + 73,5 – 40×1,5 + 11,5 = 0;
–85 + 85 = 0.
Реакции опор определены верно.
Определим значение поперечной силы Q в сечении на участке АВ, рассматривая левую часть балки. Поперечная сила в сечении численно равна алгебраической сумме всех внешних сил, действующих на рассматриваемую часть балки.
Q1 = –F = –40 кН.
Знак «минус» берется потому, что сила слева направлена вниз (см. правило знаков для Q). Поскольку Q – величина постоянная, на эпюре Q изображается в виде горизонтальной прямой.
Дальнейшее решение будем выполнять справа. Следует учесть, что знаки для Q будут обратными (см. правила знаков). Для сечения между D и С:
Q2 = –RД = –11,5 кH.
Эпюра на этом участке также изображается горизонтальной прямой. Определим Q между С и В:
Q3 = –RД + q(z3–1) = –11,5 + 30(z3–1).
Это уравнение наклонной прямой. Чтобы ее построить, определим две точки на концах участка:
z3 = 1 м, Q3 = –11,5 кН;
z3 = 2,5 м, Q3 = –11,5 + 30(2,5–l) = 33,5 кН.
Откладываем наклонную прямую по этим точкам. Она пересекает нулевую линию. В точке пересечения Q = 0, и, следовательно, эпюра моментов имеет экстремум, поэтому значение z для этой точки нужно определить.
Q3 = –11,5 + 30(z3–1) = 0;
или
z3 = 41,5/30 = 1,38 м.
Проверим эпюру Q на правильность построения. Значения Q для правой и левой части должны совпасть, если в сечении не приложена сосредоточенная сила. Если же сила приложена, то значение Q должно различаться на величину этой силы. В точке В приложена сила RВ = 73,5 кН и Q различается на эту величину.
Определим изгибающий момент на первом участке. Изгибающий момент в сечении равен алгебраической сумме всех внешних моментов, вычисленных относительно сечения и приложенных к рассматриваемой части балки:
M1 = –F×z1 = –40 z.
Это уравнение наклонной прямой.
при z1 = 0, M1 = 0;
z1 = l м, М1 = –40 кН×м.
На втором участке:
M2 = RД×z2 = 11,5 z2;
при z2 = 0, M2 = 0;
z2 = 1 м, М2 = 11,5 кН×м.
На третьем участке:
M3 = RД×z3 – q(z3 – 1)(z3 – 1)/2 – m = 11,5z3 – 15(z3 – 1)2 – 35.
Это уравнение параболы, так как z во второй степени. Для построения параболы необходимо определить 3 точки: по краям участка и экстремальное значение. Парабола строится дугой навстречу распределенной нагрузке. При:
z3 = 1 м, М3 = 11,5 – 35 = –23,5 кН×м,
z3 = 1,38 м, М3 = 11,5 – 1,38 – 15(1,38 – 1)2 – 35 = –21,3 кН×м,
z3 = 2,5 м, M3 = 11,5 – 2,5 – 15(2,5 – l)2 – 35 = –40 кH×м.
Проверим правильность построения эпюры М. Значения изгибающих моментов для левой и правой части должны совпасть, если в сечении нет внешнего момента, и различаться на величину внешнего момента, если он приложен. В сечении В нет внешнего момента, а изгибающий момент слева и справа одинаков. Следовательно, эпюра М построена правильно.
Опасным является сечение, в котором изгибающий момент максимальный без учета знака. Опасным будет сечение В, для которого
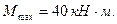
Сечение балки подбирают по формуле:
.
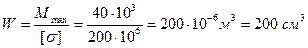По таблице сортамента, приведенной в приложении (таблица 6), находим двутавр № 20а Wх = 203 см3.
Для круглого сечения:
.
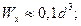
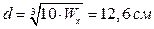Для прямоугольного сечения:
.
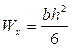По условию задачи h = 2b, поэтому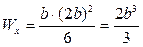 
,
откуда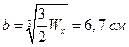 
; 
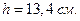
Сравнение 1 м веса балки можно произвести по площади поперечного сечения разных профилей:
− для двутавра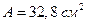 
(см. таблицу 6 приложения);
− для круга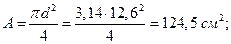 
− для прямоугольника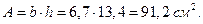 
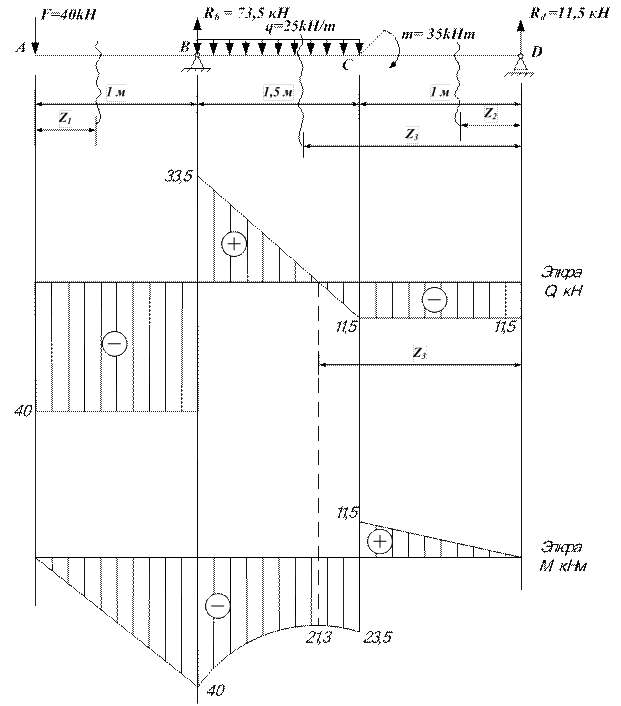
Рисунок 11 − Схема балки и эпюры внутренних усилий
Если двутавровое сечение принять за единицу, то соотношение профилей будет:
− для круглого сечения 124,5/32,8 = 3,8;
− для прямоугольного 91,2/32,8 = 2,78.
Следовательно, при использовании балки круглого сечения расход материала увеличивается в 3,8 раз, прямоугольного – в 2,78 раза.
Пример №5
Равноустойчивая стальная стойка (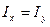 
) длиной 
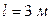сжимается силой F = 40 кН (рисунок 12). Поперечное сечение составлено из двух неравнобоких уголков (рисунок 13), материал Ст. 3,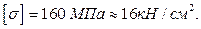 
Необходимо:
1. Определить из условия устойчивости номер уголка.
2. Найти критическую силу и коэффициент запаса устойчивости.
3. Определить из условия равноустойчивости размер с сечения.
| 
| |||
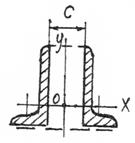
| Рисунок 12 − Схема равноустойчивой стальной стойки | Рисунок 13 − Поперечное сечение стойки |
Решение
Решение задачи осуществляют методом постепенного приближения. Зададимся первым значением коэффициента снижения основного допускаемого напряжения j1 = 0,5.
Из условия устойчивости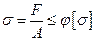 
находим требуемую площадь поперечного сечения А.
.
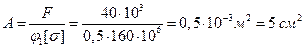Площадь уголка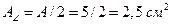 
.
По приложению таблицы 9 примем уголок 40´25´4 с площадью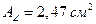 
и радиусом инерции 
.
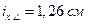Радиус инерции сечения относительно оси Х равен радиусу инерции уголка:
.
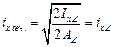Гибкость стойки l=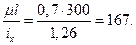 
Здесь коэффициент приведения длины для данной стойки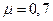 
.
Из приложения (таблица 3) по гибкости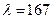 
определяем 
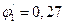, не совпадающее с 
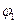, поэтому на следующем этапе примем второе значение 
.
.
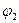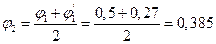А =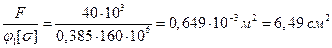 
, 
.
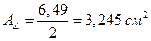Примем уголок 50´32´4,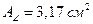 
, 
.
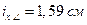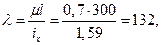по таблице 
.
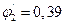Поскольку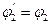 
, окончательно принимаем уголок 50´32´4 (рисунок 14) со следующими данными:
 ,
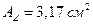| Рисунок 14 − Схема принятого уголка | |
 ,
| 
| |
 .
| 
|
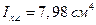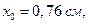
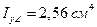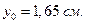
Определяем критическую силу.
Так как гибкость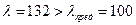 
для (Ст. 3), то критическую силу вычисляем по формуле Л. Эйлера.
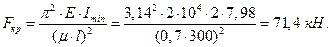
Коэффициент запаса устойчивости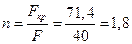 
.
Вычисляем размер с из условия равенства главных центральных моментов инерции сечения.
,
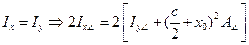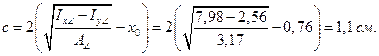
Окончательно принимаем с = 11 мм.
СПИСОК ИСПОЛЬЗОВАННОЙ
И РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Балакин, В.А. Механика материалов: Практич. пособие к решению контрольных и расчетно-графических работ по одноим. курсу для студентов днев. и заоч. форм обучения спец. мех.-техн. и машиностроит. фак. /В.А.Балакин, И.Н.Литвиненко, А.А.Иванов. – Гомель: ГГТУ им. П.О.Сухого, 2004. – 79 с.
2. Дарков, А.В., Шпиро, Г.С. Сопротивление материалов: Учеб. для втузов. – 5-е изд., перераб. и доп. – М.: Высш. школа, 1989. – 624 с.
3. Методические указания к контрольным работам по сопротивлению материалов для студентов-заочников технологических специальностей / сост. А.В. Минченко, А.В. Карпушко // Витебск: УО ВГТУ, 2001.– 52 с.
4. Михайлов, А.В. Сопротивление материалов: Учебник для техникумов. – М.: Стройиздат, 1989. – 352 с.
5. Подскребко М.Д. Сопротивление материалов: учебник / М.Д. Подскребко. – Минск: Выш.шк., 2007. – 797 с.
6. Сборник задач по сопротивлению материалов с теорией и примерами / Под ред. А.Г. Горшкова, Д.В. Тарлаковского. – М.: Физматлит, 2003.– 632 с.
7. Степин, П.А. Сопротивление материалов: Учеб. для немашиностроит. спец. вузов. – 8-е изд. – М.: Высш. школа, 1988. – 367 с.
8. Феодосьев, В.И. Сопротивление материалов: Учеб. для вузов. – 9-е изд., перераб. – М.: Наука, 1986. – 512 с.
Приложения
Таблица 1 – Греческий алфавит
| Буквы | Названия букв | Буквы | Названия букв | Буквы | Названия букв |
| A a | альфа | I i | йота | R r | ро |
| B b | бета | K k | каппа | S s | сигма |
| G g | гамма | L l | ламбда | T t | тау |
| D d | дельта | M m | мю | U u | ипсилон |
| E e | эпсилон | N n | ню | F j(f) | фи |
| Z z | дзета | X x | кси | C c | хи |
| H h | эта | O o | омикрон | Y y | Пси |
| Q q | тэта | P p | пи | W w | Омега |
Таблица 2 – Приставки СИ и множители для образования десятичных кратных и дольных единиц и их наименования
| Приставка | Обозначение приставки | Множитель | |
| международное | русское | ||
| экса | E | Э | 1018 |
| пета | P | П | 1015 |
| тера | T | Е | 1012 |
| гига | G | Г | 109 |
| мега | M | М | 106 |
| кило | k | к | 103 |
| гекто | h | г | 102 |
| дека | da | да | 101 |
| деци | d | д | 10-1 |
| санти | c | с | 10-2 |
| милли | m | м | 10-3 |
| микро | m | мк | 10-6 |
| нано | n | н | 10-9 |
| пико | p | п | 10-12 |
| фемто | f | ф | 10-15 |
| атто | a | а | 10-18 |
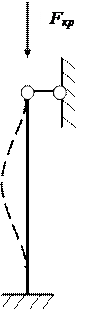
Таблица 3 − Влияние условий закрепления концов стержня на критическую силу
| С Х Е М А С Т О Й К И |
|
|
|
|
| |||
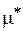
| 2 | 1 | 0,7 | 0,5 | 0,5 |
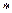− коэффициент приведения длины.
Таблица 4 − Параметры для определения критических напряжений
|
Материал |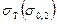 
| 
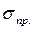
| а | b | с | Граничные значения гибкости | |
| МПа |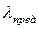 
| 
| |||||
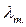
| Сталь 2 Сталь 3 Сталь 4, 20 Сталь 5, 25, 35Л Сталь 35, 45Л Сталь 45 Сталь 50, 55Л Сталь 10Г2СЛ, 14Г2, 15ГС, 14ХГС Сталь 30ХМА, 30ГСА, 40ХНМА Дюралюминий Д16Т Сосна, ель Чугун | 220 240 260 280 320 360 380 350 850 320 − − | 190 200 220 240 270 305 320 300 700 255 − − | 264 310 328 350 398 449 473 429 1000 406 29,3 776 | 0,7 1,14 1,11 1,15 1,43 1,67 1,87 1,52 5,57 2,83 1,94 1,2 | − − − − − − − − − − − 5,38 | 105 100 96 92 90 85 82 83 55 53 70 80 | 62 61 60 57 55 52 50 50 28 30 − − |
Таблица 5 − Значения коэффициента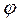 
продольного изгиба
| Гибкость
| Сталь марок | Чугун марок | Дюралю-миний Д16Т | Дерево (сосна, ель) | |||
| Ст. 3 Ст. 4 | Ст. 5 | 14Г2 15ГС 10Г2С 10Г2СД 15ХСНД | СЧ 12 СЧ 15 СЧ 18 СЧ 21 | СЧ 24 СЧ 28 | |||
| 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 | 1,00 0,99 0,97 0,95 0,92 0,89 0,86 0,81 0,75 0,69 0,60 0,52 0,45 0,40 0,36 0,32 0,29 0,26 0,23 0,21 0,19 0,17 0,16 | 1,00 0,98 0,96 0,93 0,90 0,85 0,80 0,74 0,67 0,59 0,50 0,43 0,37 0,32 0,28 0,25 0,23 0,21 0,19 0,17 0,15 0,14 0,13 | 1,00 0,98 0,95 0,92 0,89 0,84 0,78 0,71 0,63 0,54 0,46 0,39 0,33 0,29 0,25 0,23 0,21 0,19 0,17 0,15 0,13 0,12 0,11 | 1,00 0,97 0,91 0,80 0,69 0,57 0,44 0,34 0,26 0,20 0,16 − − − − − − − − − − – − | 1,00 0,95 0,87 0,75 0,60 0,43 0,32 0,23 0,18 0,14 0,12 − − − − − − − − − − – − | 1,00 0,999 0,998 0,835 0,700 0,568 0,455 0,353 0,269 0,212 0,172 0,142 0,119 0,101 0,087 0,076 − − − − − – − | 1,00 0,99 0,97 0,93 0,87 0,80 0,71 0,61 0,49 0,38 0,31 0,25 0,22 0,18 0,16 0,14 0,12 0,11 0,10 0,09 0,08 – − |
СОРТАМЕНТ ПРОКАТНОЙ СТАЛИ
Дата: 2019-05-29, просмотров: 479.
