Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Приклад 1. Вирішити рівняння .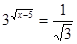

Рішення. 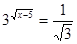;  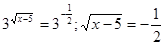- рішень немає.

Відповідь: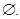

Приклад 2. Вирішити рівняння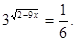

Рішення.

 

 

 

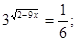
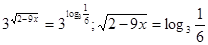
- Рішень ні, тому що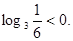

Відповідь: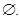

Приклад 3. Вирішити рівняння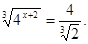

;

 

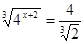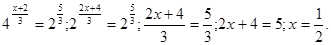
Відповідь: .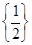

Примі 4. Вирішити рівняння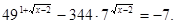

Рішення.

 

;

 

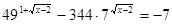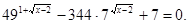
Уведемо нову змінну. Нехай 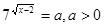. Одержуємо, що 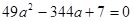. Тоді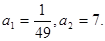

Виконаємо зворотну заміну. 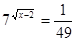 Або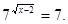

 

;

 

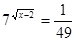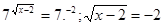
- рішень немає.

 

; .

 

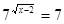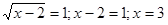Відповідь:{3}.

Приклад 5. Вирішити рівняння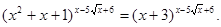

Рішення. Множина М – загальна частина (перетинання) областей існування функцій 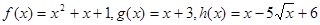- є всі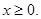

На множині М функції 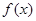 й 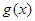 позитивні. Тому, логарифмуючи обидві частини рівняння, одержимо рівняння, рівносильне вихідному на М.

 

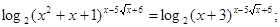
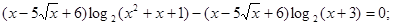
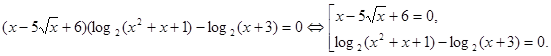
Вирішимо рівняння сукупності.

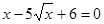. Уведемо нову змінну. Нехай 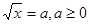. Одержуємо, що 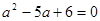. Тоді 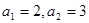. Виконаємо зворотну заміну.  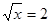або 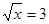. Тоді  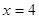або .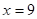

Одержуємо, що вихідне рівняння рівносильне системі:

 

 

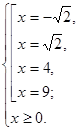
Відповідь: .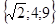

Зауваження. У задачах підвищеної складності зустрічаються рівняння виду 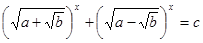, де 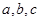- деякі позитивні числа. Такі рівняння не є ірраціональними рівняннями, тому що не містять змінної під знаком радикала, але всі, же розберемо їхнє рішення в даному пункті.

Приклад 6. Вирішити рівняння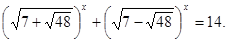

Рішення. Перетворимо вираження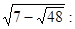

 

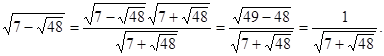
Тоді вихідне рівняння прийме вид: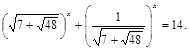

Зауваження. Можна помітити, що 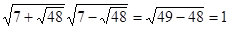, отже,  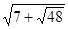і 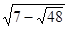- взаємно обернені числа. Тоді 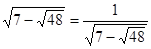. Уведемо нову змінну. Нехай 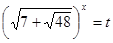, а 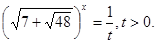Одержуємо, що вихідне рівняння рівносильне наступний 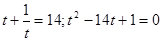. Тоді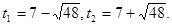

Виконаємо зворотну заміну.

 

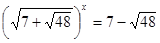 або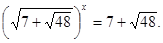

; ;

 

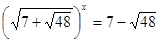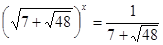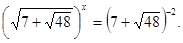
Тоді .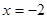

 

;

 

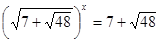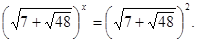
Тоді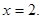

Відповідь :{-2;2}.

 

Ірраціональні логарифмічні рівняння

 

Приклад 1. Вирішити рівняння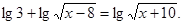

Рішення. ;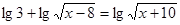

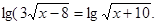
З огляду на, що 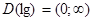, дане рівняння рівносильне системі:

 

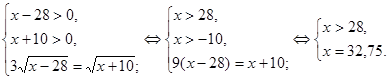
Відповідь:{32,75}.

Приклад 2. Вирішити рівняння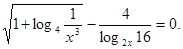

Рішення. 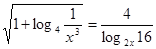. Перетворимо праву частину рівняння.

 

 

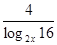
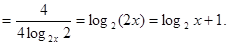
Повернемося до вихідного рівняння.

 

;

 

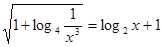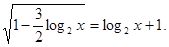
Уведемо нову змінну. Нехай 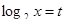. Одержуємо, що

 

.

 

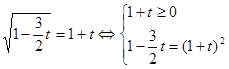Вирішимо рівняння системи.

 

; .

 

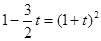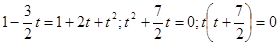Тоді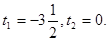

Повернемося до системи: 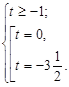Отже,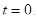

Виконаємо зворотну заміну: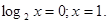

Перевірка показує, що 1 є коренем вихідного рівняння.

Відповідь: {1}.

Приклад 3. вирішити рівняння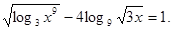

Рішення. Знайдемо ОПЗ змінної х.

ОПЗ: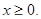

 

.

 

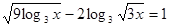На ОПЗ вихідне рівняння рівносильне рівнянню

 

; ;

 

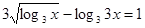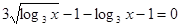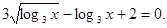
Уведемо нову змінну. Нехай 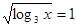 або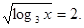

 

;

;

 

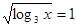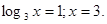
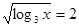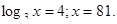
Відповідь: {3;81}.

 

Висновок

 

Дана курсова робота допомогла мені навчитися вирішувати ірраціональні рівняння наступних типів: стандартного, нестандартного, показового, логарифмічні, підвищеного рівня. Застосовувати основні властивості функції, область визначення, область значення функції. Використовувати найбільше й найменше значення функції. Застосування похідної. Я вважаю, що цілі які поставлені перед виконанням курсової роботи виконані.

 

Література

 

1. Харкова О.В. Ірраціональні рівняння. – К., 2004

2. Колмогоров О.М. Алгебра й початок аналізу. – К., 2003

3. Куланін Е.Д., Норін В.П. 3000 конкурсних задач по математиці. – К., 2000

4. Гусєв В.А., Мордкович А.Д. Довідкові матеріали по математиці. – К., 2003

5. Сканаві М.М. Збірник задач по математиці. – К., 2006