Існують ірраціональні рівняння, які вважаються для школярів звичайних освітніх шкіл задачами підвищених труднощів. Для рішення таких рівнянь краще застосовувати не традиційні методи, а прийоми, які не зовсім звичні для учнів. У цій главі приводяться рішення рівнянь заснованих на графічних міркувань, властивостях функції (таких, як монотонність, обмеженість, парність), застосуванні похідній і т.д.

Застосування основних властивостей функції

Використання області визначення рівняння

Іноді знання області визначення рівняння дозволяє довести, що рівняння не має рішень, а іноді дозволяє знайти рішення рівняння безпосередньою підстановкою чисел з її.

Приклад 1. Вирішити рівняння .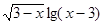

Рішення. Знайдемо область визначення рівняння.

ОПЗ: .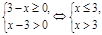

Отже, дана система рішень не має.

Так як система рішень не має, то й дане рівняння не має корінь.

Відповідь: .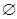

Приклад 2. Вирішити рівняння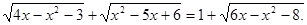

Рішення. Знайдемо ОПЗ змінної х.

ОПЗ: .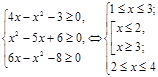

Отже, 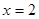 або .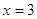

Таким чином, рішення даного рівняння можуть перебувати серед знайдених двох чисел.

Перевіркою переконуємося, що тільки 2 є коренем вихідного рівняння.

Відповідь: {2}.

Використання області значень рівнянь

Приклад 1. Вирішити рівняння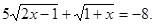

Рішення.. 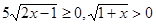, отж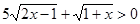е, , але 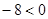 (права частина рівняння негативна, а ліва позитивна), значить дане рівняння не має рішень.

Відповідь: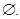

Приклад 2. Вирішити рівняння .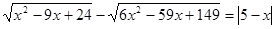

Рішення. 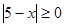, те

; ; ; ; ; ; .

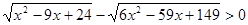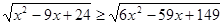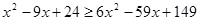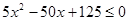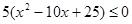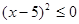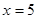Отже, ліва частина рівняння приймає ненегативне значення тільки при 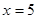. А це значить, що його коренем може бути тільки значення 5, а може трапитися, що рівняння взагалі не буде мати корінь. Для рішення цього питання виконаємо перевірку.

Перевірка показує, що 5 є коренем вихідного рівняння.

Відповідь: {5}.

3.1.3 Використання монотонності функції

Рішення рівнянь і нерівностей з використанням властивостей монотонності ґрунтується на наступних твердженнях.

1. Нехай f(x) - безперервна й строго монотонна функція на проміжку Q, тоді рівняння f(x)=c, де c - дана константа може мати не більше одного рішення на проміжку Q.

2. Нехай f(x) і g(x) - безперервні на проміжку Q функції, f(x) - строго зростає, а g(x)- строго убуває на цьому проміжку, тоді рівняння f(x)= g(x) може мати не більше одного рішення на проміжку Q.

Відзначимо, що в кожному з випадків проміжки Q можуть мати один з видів: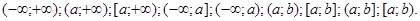

Приклад 1. Вирішимо рівняння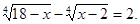

Рішення. Знайдемо ОПЗ змінної х.

ОПЗ: .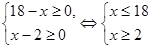

Отже, .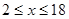

На ОПЗ функції 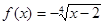 й 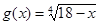 безперервні й строго убувають, отже, безперервна й убуває функція 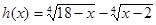. Тому кожне своє значення функція h(x) приймає тільки в одній крапці. Так як h(2)=2 , те 2 є єдиним коренем вихідного рівняння.

Відповідь: {2}.