Цель занятия – приобрести практические навыки расчета параметров и характеристик синхронных машин.
Задача 7.1
Синхронный трехфазный генератор номинальной мощностью S н=10000кВа работает с коэффициентом мощности cosφ = 0,8 при напряжении U = 6,3 кВ. Обмотки генератора соединены звездой. Активное и синхронное индуктивное сопротивления обмотки одной фазы соответственно rя = 0,04 Ом, хя = 1,0 Ом. Число пар полюсов р = 2. Мощности потерь рв = 1,3% Рн, Рмех + Рст = 1,4% Рн.
Частота сети f = 50 Гц.
Определить: скорость вращения п, э.д.с. Е, к. п. д. h генератора; мощность Р1н турбины, приводящей во вращение генератор.
Построить векторную диаграмму.
Решение
Скорость вращения генератора п для получения тока с частотой f = 50 Гц должна быть:
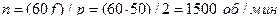
Э.д.с. генератора равна геометрической сумме напряжения на его зажимах и падения напряжения в якоре:
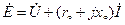 (7.1.1)
(7.1.1)
Ток генератора при номинальном режиме
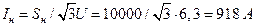 (7.1.2)
(7.1.2)
Активное и реактивное падения напряжения в обмотке одной фазы генератора соответственно:
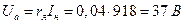 или
или 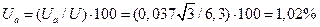 ,
,
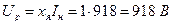 или
или 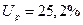
Теперь у нас есть все данные для построения векторной диаграммы (рис. 7.1.1). Выбираем масштаб т U — 20 В/мм. Откладываем вектор напряжения 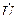 и под углом φ к нему вектор тока
и под углом φ к нему вектор тока 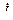 н. Из конца вектора
н. Из конца вектора 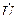 , параллельно вектору тока, откладываем вектор
, параллельно вектору тока, откладываем вектор 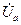 , равный активному падению напряжения
, равный активному падению напряжения 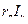 . К его концу добавляем перпендикулярно вектору тока
. К его концу добавляем перпендикулярно вектору тока 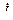 н вектор реактивного падения напряжения
н вектор реактивного падения напряжения 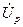 . Суммарный вектор равен фазному значению э.д.с.
. Суммарный вектор равен фазному значению э.д.с.
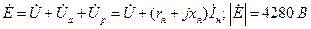 (7.1.3)
(7.1.3)
Магнитный поток Ф, индуктирующий эту э.д.с, опережает ее на 90°.
Теперь определим Е аналитически:
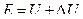 (7.1.4)
(7.1.4)
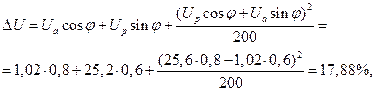
т. е.
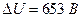
Следовательно, Е 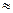 4300 В.
4300 В.
Разница в значениях э.д.с, полученных при помощи векторной диаграммы и аналитическим расчетом, составит 0,4%.
В дальнейших задачах будем использовать приближенную формулу определения э.д.с. генератора, учитывая ее сравнительно небольшую и вполне допустимую для расчетов погрешность.
К. п. д. генератора определим из соотношения:
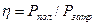 , (7.1.5)
, (7.1.5)
где 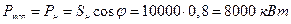 – полезная мощность, т. е. мощность на зажимах генератора.
– полезная мощность, т. е. мощность на зажимах генератора.
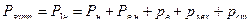 – затраченная мощность.
– затраченная мощность.
В свою очередь 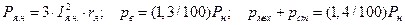
Итак, при номинальной нагрузке генератора
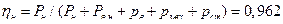
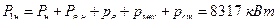
Задание для самостоятельной работы
Исходные данные определить согласно формул:
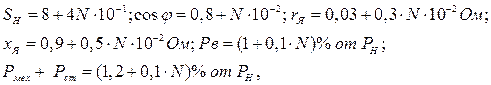
где N – последняя цифра зачетной книжки.
Задача 7.2
Определить ток и напряжение генератора, если активная и реактивная мощности его нагрузки Р = 3500 кВт, Q = 1500 кВар, э.д.с. Е = 6,72 кВ, активное и синхронное индуктивное сопротивления якоря r я = 0,14 Ом, хя = 2 Ом.
Обмотки якоря соединены звездой.
Решение
Весь расчет будем проводить для одной фазы. Определяем фазную э.д.с.
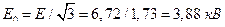 (7.2.1)
(7.2.1)
Полная мощность нагрузки
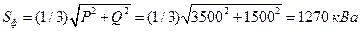 (7.2.2)
(7.2.2)
Коэффициент мощности нагрузки
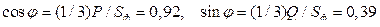
Для определения фазного напряжения воспользуемся формулой:
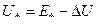 , (7.2.3)
, (7.2.3)
где 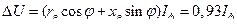 .
.
Из уравнения 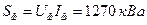 , находим, что
, находим, что 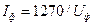 .
.
Следовательно, 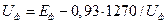 .
.
Откуда 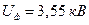 .
.
Напряжение генератора
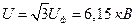
При соединении обмоток якоря звездой
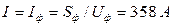
Задание для самостоятельной работы
Исходные данные определить согласно формул:
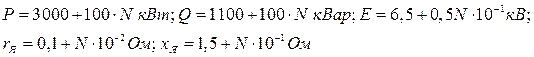
где N – последняя цифра зачетной книжки.
Задача 7.3
Два однотипных трехфазных генератора работают параллельно при напряжении U = 3,3 кВ. Мощность потребителя Р = 8000 кВ m при cosφ = 0,8 распределяется между генераторами поровну.
Определить фазную э.д.с. генераторов при равномерно распределенной нагрузке и в случае, если вся нагрузка будет переведена на один генератор. Напряжение на шинах поддерживается неизменным. Активное сопротивление якоря r я = 0,04Ом, синхронное индуктивное сопротивление хя = 0,7Ом.
Обмотки якоря соединены звездой.
Решение
Э.д.с. генератора при равномерно распределенной нагрузке определяем по формуле:
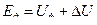 (7.3.1)
(7.3.1)
где 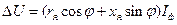
В свою очередь 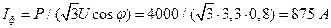
Следовательно, 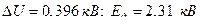
Если вся нагрузка будет переведена на один генератор, то потеря напряжения у него будет в два раза больше и э.д.с. Возрастает до значения 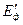 :
:
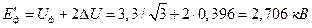
ЛИТЕРАТУРА
1. Бессонов Л.А. Теоретические основы электротехники, электрические цепи. Часть I, 8-е изд., М: Высшая школа, 1987.-559с.
2. Герасимов В.Г. Электротехника. М.: Высшая школа, 1985.-480с.
3. Пономаренко В. К. Сборник задач с решениями по общей электротехнике. М.: Высшая школа, 1972.-184с.
4. Рекус Г.Г. Сборник задач и упражнений по электротехнике и основам электроники: Учебное пособие для неэлектротехнических специальностей вузов.-2-е изд. перераб.–М.: Высшая школа, 2001.–416с.
5. Трегуб А.П. Электротехника. М: Высшая школа, 1987.-600с.
6. Нейман Л.Р., Демирчан К.С. Теоретические основы электротехники. Часть 1,2.–Л.: Энергоиздат, 1981.-522с.
Солодилова Валентина Вячеславовна
Ибрагимов Олег Эрастович
Савенко Александр Евгеньевич
Электротехника
Дата: 2019-04-22, просмотров: 912.