Цель занятия – приобрести практические навыки расчета и анализа цепей синусоидального тока с последовательным соединением элементов, цепей синусоидального тока с параллельным соединением элементов, приобрести краткие навыки расчета и анализа сложных цепей синусоидального тока.
Задача 2.1
Для последовательной цепи переменного тока с индуктивной катушкой и конденсатором (рисунок 2.1.1) задано:
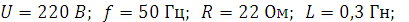
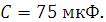
 Определить сопротивления, cosφ, ток и напряжения на участках цепи, а также построить диаграмму и треугольник сопротивлений.
Определить сопротивления, cosφ, ток и напряжения на участках цепи, а также построить диаграмму и треугольник сопротивлений.
Решение
Сопротивление цепи:
· Индуктивное сопротивление:
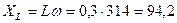 Ом (2.1.1)
Ом (2.1.1)
· Полное сопротивление катушки:
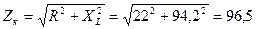 Ом (2.1.2)
Ом (2.1.2)
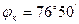
· Емкостное сопротивление:
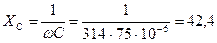 Ом (2.1.3)
Ом (2.1.3)
· Полное сопротивления цепи:
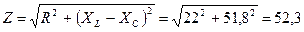 Ом(2.1.4)
Ом(2.1.4)
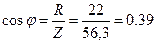 ,
, 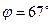
Ток и напряжения на цепи:
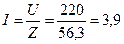 А, (2.1.5)
А, (2.1.5)
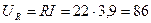 В, (2.1.6)
В, (2.1.6)
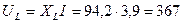 В, (2.1.7)
В, (2.1.7)
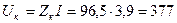 В, (2.1.8)
В, (2.1.8)
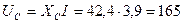 В, (2.1.9)
В, (2.1.9)
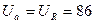 В,
В,
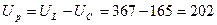 В (2.1.10)
В (2.1.10)
Примерная векторная диаграмма и треугольник сопротивлений цепи (без масштаба) показана на рис. 2.1.3.

Задание для самостоятельной работы
Исходные данные определить согласно формул:
R = 20 + N Ом, L = 0.01N Гн, C = 15N мкФ, U = 200 +N В, f = 50 Гц.
Где N – номер по списку журнала.
Задача 2.2
Для последовательной цепи переменного тока с индуктивной катушкой и конденсатором (рис. 2.2.1) задано: U=220 В; f=50 Гц; R =22 Ом; L=0,3 Гн; С=75 мкФ. Найти поочередно значения, при которых в цепи на рис наступит режим резонанса напряжений, определив при этом токи и напряжения элементов цепи.
Решение
Чтобы получить резонанс напряжений в цепи при заданных C и f , необходимо уменьшить индуктивное сопротивление до значения 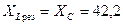 Ом. Отсюда искомая индуктивность катушки:
Ом. Отсюда искомая индуктивность катушки:

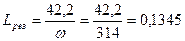 Гн (2.2.1)
Гн (2.2.1)
В этом режиме резонанса:
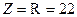 Ом,
Ом, 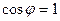 ,
, 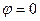 ,
,
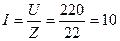 А,
А, 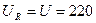 В, (2.2.2)
В, (2.2.2)
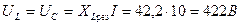 (2.2.3)
(2.2.3)
 Векторная диаграмма цепи показана на рисунке 2.2.2.
Векторная диаграмма цепи показана на рисунке 2.2.2.
Для резонанса напряжений в той же цепи при заданных 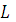 и
и 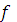 нужно уменьшить емкость, т.е. увеличить
нужно уменьшить емкость, т.е. увеличить 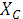 до заданного значения
до заданного значения 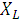 :
:
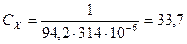 мкФ (2.2.4)
мкФ (2.2.4)
В этом режиме резонанса:
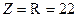 Ом,
Ом, 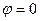 ,
, 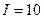 А,
А, 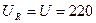 В
В
При заданных I и C резонансная частота входного напряжения С уменьшением частоты сети с 50 до 33,6 Гц индуктивное сопротивление цепи уменьшается, а емкостное – увеличивается.
В режиме резонанса:
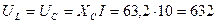 В
В
Задание для самостоятельной работы
Исходные данные определить согласно формул:
R = 20 + N Ом, L = 0.01N Гн, C = 15N мкФ, U = 200 +N В, f = 50 Гц.,
где N – номер по списку журнала.
Задача 2.3
Для неразветвленной цепи (рис. 2.3.1) определить ток и напряжения на всех элементах, а также построить векторную диаграмму, если 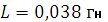 ,
, 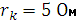 ,
, 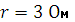 ,
, 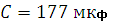 ,
, 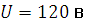 . Частота тока
. Частота тока 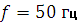 .
.
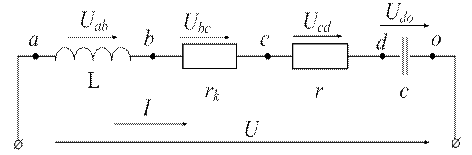
Рисунок 2.3.1 - Электрическая схема последовательного соединения индуктивной
катушки, конденсатора и активного сопротивления.
Решение
Определим сопротивления цепи:
· индуктивное 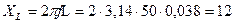 Ом (2.3.1)
Ом (2.3.1)
· ёмкостное 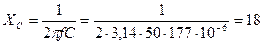 Ом (2.3.2)
Ом (2.3.2)
· полное 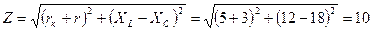 Ом (2.3.3)
Ом (2.3.3)
Ток в цепи
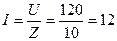 А (2.3.4)
А (2.3.4)
Напряжения на отдельных элементах цепи:
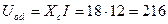 В,
В,
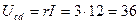 В,
В,
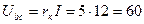 В,
В,
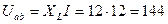 В
В
Для построения векторной диаграммы выберем масштаб:
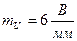 ,
, 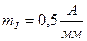 .Масштабы удобно выбирать таким образом, чтобы в единице длины было 1, 2, 5 единиц измерения изображаемой физической величины, или одного из этих трех чисел, умноженное на
.Масштабы удобно выбирать таким образом, чтобы в единице длины было 1, 2, 5 единиц измерения изображаемой физической величины, или одного из этих трех чисел, умноженное на 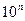 , где n – любое целое положительное или отрицательное число.
, где n – любое целое положительное или отрицательное число.
Итак, векторная диаграмма в выбранном масштабе постоянно на рисунке 2.3.2. Векторы напряжений на активных сопротивлениях 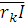 и
и 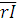 совпадают по направлению с вектором тока
совпадают по направлению с вектором тока 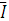 , вектор
, вектор 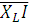 опережает, а вектор
опережает, а вектор 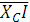 отстает от вектора тока
отстает от вектора тока 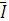 на четверть периода. Вектор напряжения на зажимах цепи равен геометрической сумме напряжения на всех ее элементах. Все векторы начинаются в точке 0.
на четверть периода. Вектор напряжения на зажимах цепи равен геометрической сумме напряжения на всех ее элементах. Все векторы начинаются в точке 0.
Угол сдвига фаз 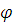 в цепи:
в цепи:
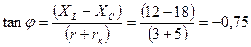 (2.3.5)
(2.3.5)
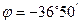
 Знак угла
Знак угла 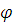 отрицательный, так как ток
отрицательный, так как ток 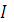 опережает по фазе напряжение
опережает по фазе напряжение 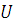 .
.
Угол 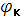 , на которой вектор напряжения на катушке опережает вектор тока
, на которой вектор напряжения на катушке опережает вектор тока 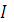 , определяется по формуле:
, определяется по формуле:
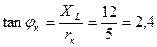 ,
, 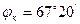
Напряжение 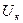 на катушке
на катушке
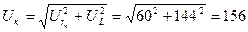 В
В
Или
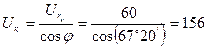 В
В
Задание для самостоятельной работы.
Исходные данные определить согласно формул:
R = 20 + N Ом, L = 0.01N Гн, C = 15N мкФ, U = 200 +N В, f = 50 Гц.,
где N – номер по списку журнала.
Задача 2.4
Определить ток в цепи (рис.2.4.1) и напряжения на ее элементах, если 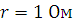
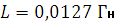 ,
, 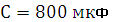 ,
, 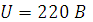 , частота тока
, частота тока 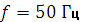 .
.
Построить векторную диаграмму.

Решение
В данной схеме индуктивное сопротивление 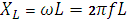 равно емкостному сопротивлению
равно емкостному сопротивлению 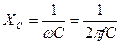 и полное сопротивление цепи
и полное сопротивление цепи
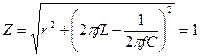 Ом (2.4.1)
Ом (2.4.1)
Ток в цепи
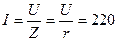 А (2.4.2)
А (2.4.2)
Коэффициент мощности
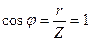 (2.4.3)
(2.4.3)
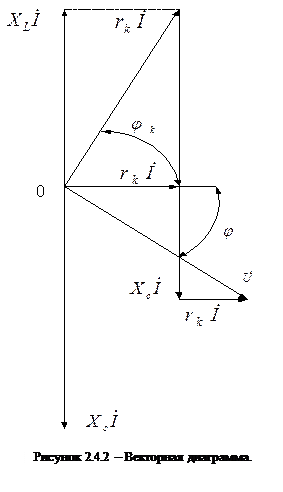 Активная мощность
Активная мощность
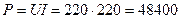 Вт (2.4.4)
Вт (2.4.4)
Такой режим носит название резонанса напряжений.
Величина тока 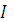 при резонансе напряжений зависит только от напряжения
при резонансе напряжений зависит только от напряжения 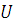 и величины активного сопротивления
и величины активного сопротивления 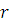 .
.
Напряжение на индуктивности 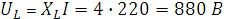 и напряжение на емкости
и напряжение на емкости 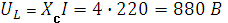 , противоположные по фазе, уравновешивают друг друга и их разность равна нулю.
, противоположные по фазе, уравновешивают друг друга и их разность равна нулю.
На рис (2.4.2) построена векторная диаграмма в масштабе.
Так как величина реактивных сопротивлений 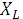 и
и 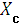 зависит от частоты f, то подборкой параметров L и C можно создать условия для резонанса напряжений при частоте, определяемой выражением:
зависит от частоты f, то подборкой параметров L и C можно создать условия для резонанса напряжений при частоте, определяемой выражением:
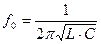 (2.4.5)
(2.4.5)
В данном случае
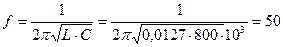 Гц
Гц
Задание для самостоятельной работы
Исходные данные определить согласно формул:
r = 1 + N Ом, L = 0.0120 + 0.001N Гн, C = 100N мкФ, U = 200 +N В, f = 50 Гц,
где N – номер по списку журнала.
Задача 2.5
Определить токи и напряжение 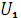 в цепи (рис.2.5.1), построить векторную диаграмму, определить угол сдвига фаз между током
в цепи (рис.2.5.1), построить векторную диаграмму, определить угол сдвига фаз между током 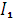 и напряжением
и напряжением 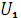 из векторной диаграммы, если напряжение U 2 =220 B, емкостное сопротивление конденсатора X С = 44 Ом, индуктивное сопротивление катушки X L = 24 Ом, активное сопротивление R 3 = 4.5 Ом, активное сопротивление катушки. R 1 = 39 Ом, R 0 = 7 Ом.
из векторной диаграммы, если напряжение U 2 =220 B, емкостное сопротивление конденсатора X С = 44 Ом, индуктивное сопротивление катушки X L = 24 Ом, активное сопротивление R 3 = 4.5 Ом, активное сопротивление катушки. R 1 = 39 Ом, R 0 = 7 Ом.
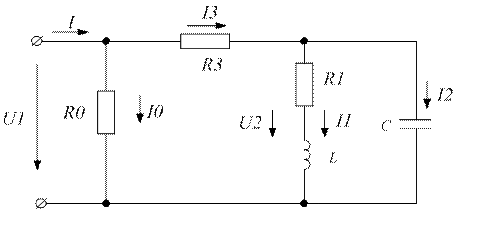
Рисунок 2.5.1 – Электрическая схема смешанного соединения индуктивной катушки,
емкости и активного сопротивления.
Решение
Ток в ветви конденсатора 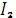 опережает по фазе напряжение
опережает по фазе напряжение 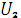 на четверть периода.
на четверть периода.
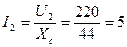 В (2.5.1)
В (2.5.1)
Полное сопротивление ветви катушки
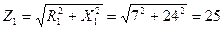 Ом (2.5.2)
Ом (2.5.2)
Ток в ней
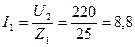 А (2.5.3)
А (2.5.3)
Ток 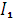 отстает по фазе от напряжение
отстает по фазе от напряжение 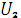 на угол, тангенс которого равен отношению реактивного сопротивления к активному:
на угол, тангенс которого равен отношению реактивного сопротивления к активному:
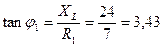 , (2.5.4)
, (2.5.4)
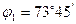
Вектор тока 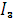 равен сумме векторов токов
равен сумме векторов токов 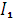 и
и 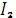 .
.
Учитывая, что ток 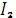 является реактивным, опережающим
является реактивным, опережающим 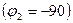 , а ток
, а ток 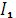 имеет две компоненты:
имеет две компоненты:
· активную
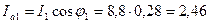 А (2.5.5)
А (2.5.5)
· реактивную
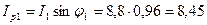 А (2.5.6)
А (2.5.6)
Определим ток 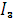 :
:
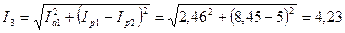 А (2.5.7)
А (2.5.7)
Напряжение 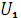 можно определить аналитически, но для упражнения найдем его из векторной диаграммы (рис.), при построении которой был выбран масштаб:
можно определить аналитически, но для упражнения найдем его из векторной диаграммы (рис.), при построении которой был выбран масштаб: 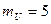 В/мм,
В/мм, 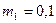 А/мм
А/мм
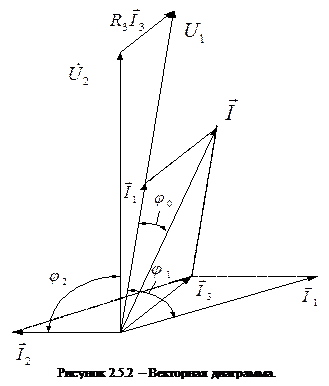 Вектор напряжения равен сумме векторов напряжения
Вектор напряжения равен сумме векторов напряжения 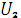 и активного напряжения
и активного напряжения 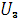 на сопротивление
на сопротивление 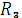 :
:
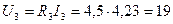 В (2.5.8)
В (2.5.8)
Напряжение 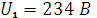 .
.
Ток в сопротивлении 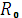
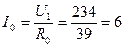 А
А
Он совпадает по фазе с напряжением 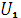 . Вектор тока
. Вектор тока 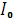 откладывается на диаграмме по направлению,
откладывается на диаграмме по направлению,
совпадающему с направлением вектора напряжения 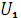 .
.
Вектор суммарного тока 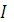 можно определить аналитически по методу проводимости или из векторной диаграммы сложением векторов токов
можно определить аналитически по методу проводимости или из векторной диаграммы сложением векторов токов 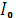 и
и 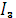 .
.
Ток 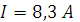 .
.
Угол сдвига фаз между 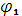 током
током 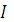 и напряжением
и напряжением 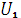 определяем из векторной диаграммы:
определяем из векторной диаграммы:
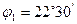
Задание для самостоятельной работы.
Исходные данные определить согласно формул:
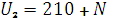 ,
, 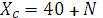 ,
, 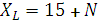 ,
, 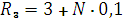
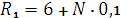 ,
,
где N – номер по списку журнала.
Задача 2.6
В сеть напряжением 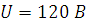 и частотой
и частотой 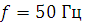 включена индуктивная катушка сопротивлением
включена индуктивная катушка сопротивлением 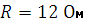 и индуктивностью
и индуктивностью 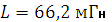 . Ее последовательная схема замещения изображена на рис. определить комплексный ток, значения полной, активной и реактивной мощности. Построить топографическую диаграмму напряжений, треугольники сопротивлений и мощностей. Вектор тока и топографическая диаграмма напряжений построены на рисунке 2.6.2
. Ее последовательная схема замещения изображена на рис. определить комплексный ток, значения полной, активной и реактивной мощности. Построить топографическую диаграмму напряжений, треугольники сопротивлений и мощностей. Вектор тока и топографическая диаграмма напряжений построены на рисунке 2.6.2


Решение
Индуктивное сопротивление катушки
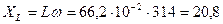 Ом (2.6.1)
Ом (2.6.1)
Полное сопротивление:
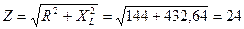 Ом (2.5.2)
Ом (2.5.2)
Ток в цепи:
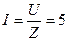 А (2.6.3)
А (2.6.3)
Полная мощность:
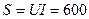 ВА (2.6.4)
ВА (2.6.4)
Активная мощность:
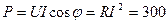 Вт (2.6.5)
Вт (2.6.5)
Реактивная индуктивная мощность:
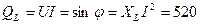 Вар (2.6.6)
Вар (2.6.6)
Напряжение на активном элементе:
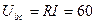 В (2.6.7)
В (2.6.7)
Напряжение на индуктивном элементе:
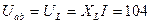 В (2.6.8)
В (2.6.8)
Задание для самостоятельной работы
Исходные данные определить согласно формул:
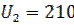 ,
, 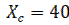 ,
, 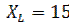 ,
, 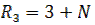 ,
, 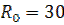 ,
, 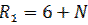 ,
,
где N – последняя цифра зачетной книжки.
Задача 2.7
В электрической цепи переменного тока напряжения и тока изменяется во времени в соответствии с выражениями 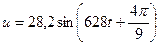 В,
В, 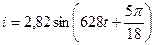 А. Определить активную
А. Определить активную 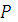 , реактивную
, реактивную 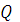 и полную
и полную 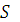 мощности цепи.
мощности цепи.
Решение
Мгновенное значение мощности цепи:
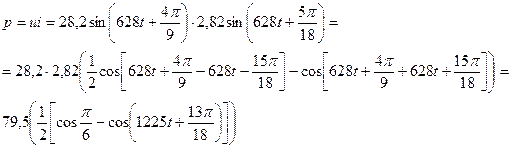 (2.7.1)
(2.7.1)
или для действующих значений тока и напряжения:
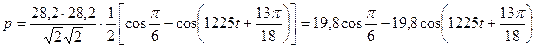 (2.7.2)
(2.7.2)
Мощности цепи:
активная:
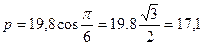 Вт (2.7.3)
Вт (2.7.3)
реактивная:
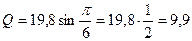 Вар (2.7.4)
Вар (2.7.4)
полная:
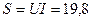 ВА (2.7.5)
ВА (2.7.5)
Дата: 2019-04-22, просмотров: 436.