Общепризнанным следует считать тот факт, что с течением времени на предприятии, сохраняющем фиксированную численность работников и постоянный объем основных фондов, выпуск продукции увеличивается. Это означает, что помимо обычных производственных факторов, связанных с затратами ресурсов, существует фактор, который обычно называют научно-техническим прогрессом (НТП). Этот фактор можно рассматривать как синтетическую характеристику, отражающую совместное влияние на экономический рост многих существенных явлений, среди которых нужно отметить следующие:
а) улучшение со временем качества рабочей силы вследствие повышения квалификации работников и освоения ими методов использования более совершенной техники;
б) улучшение качества машин и оборудования приводит к тому, что определенная сумма капитальных вложений (в неизменных ценах) позволяет по прошествии времени приобрести более эффективную машину;
в) улучшение многих сторон организации производства, в том числе снабжения и сбыта, банковских операций и других взаимных расчетов, развитие информационной базы, образование различного рода объединений, развитие международной специализации и торговли и т.п.
В связи с этим термин научно-технический прогресс можно интерпретировать как совокупность всех явлений, которые при фиксированных количествах затрачиваемых производственных факторов дают возможность увеличить выпуск качественной, конкурентоспособной продукции. Весьма расплывчатый характер такого определения приводит к тому, что исследование влияния НТП проводится лишь как анализ того дополнительного увеличения продукции, которое не может быть объяснено чисто количественным ростом производственных факторов. Главный подход к учету НТП сводится к тому, что в совокупность характеристик выпуска или затрат вводится время ( t ) как независимый производственный фактор и рассматривается преобразование во времени либо производственной функции, либо технологического множества.
Остановимся на способах учета НТП путем преобразования производственной функции (ПФ), причем за основу примем двухфакторную ПФ:
где в качестве производственных факторов выступают капитал ( К ) и труд ( L ). Модифицированная ПФ в общем случае имеет вид
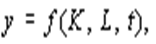
причем выполняется условие
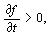
которое и отражает факт роста производства во времени при фиксированных затратах труда и капитала. Геометрическая иллюстрация такого процесса дана на рис. 4.13, где показано, что изокванта, соответствующая выпуску продукции в объеме Q , смещается с течением времени ( t 2 > t 1 ) вниз и налево.
При разработке конкретных модифицированных ПФ обычно стремятся отразить характер НТП в наблюдаемой ситуации. При этом различают четыре случая:
а) существенное улучшение со временем качества рабочей силы позволяет добиться прежних результатов с меньшим количеством занятых; подобный вид НТП часто называют трудосберегающим. Модифицированная ПФ имеет вид
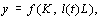где монотонная функция l ( t ) характеризует рост производительности труда;
Рис. 13. Рост производства во времени при фиксированных затратах труда и капитала
б) преимущественное улучшение качества машин и оборудования повышает фондоотдачу, имеет место капиталосберегающий НТП и соответствующая ПФ:
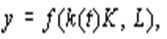
где возрастающая функция k ( t ) отражает изменение фондоотдачи;
в) если имеет место значительное влияние обоих упомянутых явлений, то используется ПФ в форме
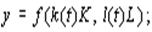
г) если же нет возможности выявить влияние НТП на производственные факторы, то применяется ПФ в виде
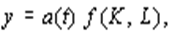
где a ( t ) возрастающая функция, выражающая рост продукции при неизменных значениях затрат факторов. Для исследования свойств и особенностей НТП используются некоторые соотношения между результатами производства и затратами факторов. К их числу относятся:
а) средняя производительность труда
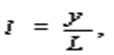
б) средняя фондоотдача
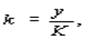
в) коэффициент фондовооруженности работника
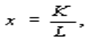
г) равенство между уровнем оплаты труда и предельной (маргинальной) производительности труда
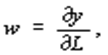
д) равенство между предельной фондоотдачей и нормой банковского процента
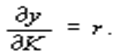
Говорят, что НТП является нейтральным, если он не изменяет с течением времени определенных связей между приведенными величинами.
Рассмотрим далее три случая:
1) прогресс называется нейтральным по Хиксу, если в течение времени остается неизменным соотношение между фондовооруженностью ( x ) и предельной нормой замены факторов ( w / r ). В частности, если w / r = const, то замена труда на капитал и наоборот не принесет никакой выгоды и фондовооруженность x = K / L также останется постоянной. Можно показать, что в этом случае модифицированная ПФ имеет вид
,
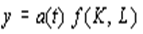и нейтральность по Хиксу эквивалентна рассмотренному выше влиянию НТП непосредственно на выпуск продукции. В рассматриваемой ситуации изокванта с течением времени смещается налево вниз путем преобразования подобия, т.е. остается в точности той же формы, что и в исходном положении;
2) прогресс называется нейтральным по Харроду, если в течение рассматриваемого периода времени норма банковского процента ( r ) зависит лишь от фондоотдачи ( k ), т.е. на нее не влияет НТП. Это означает, что предельная фондоотдача установлена на уровне нормы процента и дальнейшее увеличение капитала нецелесообразно. Можно показать, что такой тип НТП соответствует производственной функции
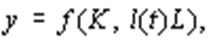
т.е. технический прогресс является трудосберегающим;
3) прогресс является нейтральным по Солоу, если сохраняется неизменным равенство между уровнем оплаты труда ( w ) и предельной производительностью труда и дальнейшее увеличение затрат труда невыгодно. Можно показать, что в этом случае ПФ имеет вид
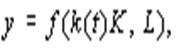
т.е. НТП оказывается фондосберегающим. Дадим графическое представление трех типов НТП на примере линейной производственной функции
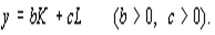
В случае нейтральности по Хиксу имеем модифицированную ПФ
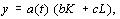
где a ( t ) возрастающая функция t . Это означает, что с течением времени изокванта Q (отрезок прямой АВ ) смещается к началу координат параллельным переносом (рис. 14) в положение A 1 B 1 .
В случае нейтральности по Харроду модифицированная ПФ имеет вид
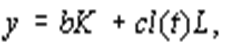
где l ( t ) возрастающая функция.
Очевидно, что с течением времени точка А остается на месте и изокванта смещается к началу координат при помощи поворота в положение AB 1 (рис. 15).
Для прогресса, нейтрального по Солоу, соответствующая модифицированная ПФ
где k ( t ) возрастающая функция. Изокванта смещается к началу координат, но точка В не сдвигается, и происходит поворот в положение A 1 B (рис. 16).
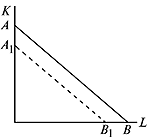Рис. 14. Сдвиг изокванты при нейтральном НТП по Хиксу
| 
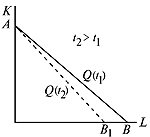Рис. 15. Сдвиг изокванты при трудосберегающем НТП
| 
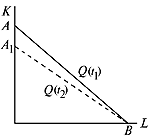Рис. 16. Сдвиг изокванты при фондосберегающем НТП
|
При построении моделей производства с учетом НТП в основном используются следующие подходы:
а) представление об экзогенном (или автономном) техническом прогрессе, который существует также в том случае, когда основные производственные факторы не изменяются. Частным случаем такого НТП является нейтральный прогресс по Хиксу, который обычно учитывается с помощью экспоненциального множителя, например:
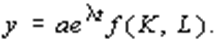
Здесь l > 0, характеризует темп НТП. Нетрудно видеть, что время здесь выступает как независимый фактор роста производства, однако при этом создается впечатление, что НТП происходит сам по себе, не требуя дополнительных затрат труда и капиталовложений;
б) представление о техническом прогрессе, овеществленном в капитале, связывает рост влияний НТП с ростом капитальных вложений. Для формализации этого подхода за основу берется модель прогресса, нейтрального по Солоу:
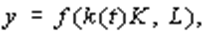
которая записывается в виде
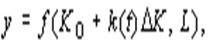
где K 0 основные фонды на начало периода,D K накопление капитала в течение периода, равное сумме инвестиций.
Очевидно, что если инвестирование не производится, тоD K = 0, и увеличение выпуска продукции за счет НТП не происходит;
в) рассмотренные выше подходы к моделированию НТП обладают общей чертой: прогресс выступает как заданная экзогенно величина, которая влияет на производительность труда или фондоотдачу и посредством этого сказывается на экономическом росте.
Однако в долгосрочном плане НТП является и результатом развития, и, в значительной мере, его причиной. Поскольку именно экономическое развитие позволяет богатым обществам финансировать создание новых образцов техники, а затем уже пожинать плоды научно-технической революции. Поэтому вполне правомерен подход к НТП как эндогенному явлению, вызванному (индуцированному) экономическим ростом.
Здесь выделяются два основных направления моделирования НТП:
1) модель индуцированного прогресса основана на формуле
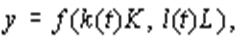
причем предполагается, что общество может распределять предназначенные для НТП инвестиции между его различными направлениями. Например, между ростом фондоотдачи ( k ( t )) (улучшение качества машин) и ростом производительности труда ( l ( t )) (повышение квалификации работников) или выбором наилучшего (оптимального) направления технического развития при данном объеме выделенных капитальных вложений;
2) модель процесса обучения в ходе производства, предложенная К. Эрроу, основана на наблюдаемом факте взаимного влияния роста производительности труда и количества новых изобретений. В ходе производства работники приобретают опыт, и время на изготовление изделия уменьшается, т.е. производительность труда и сам трудовой вклад зависят от объема производства
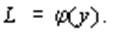
В свою очередь, рост трудового фактора, согласно производственной функции
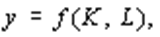
приводит к росту производства. В простейшем варианте модели используются формулы:
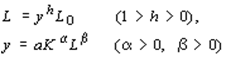
(производственная функция Кобба - Дугласа).
Отсюда имеем соотношение
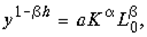
которое при заданных функциях K ( t ) и L 0 ( t ) показывает более быстрый рост y , обусловленный отмеченным выше взаимным влиянием НТП и экономического развития.
Пусть, например: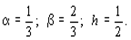 
Тогда рост без учета взаимного влияния описывается уравнением
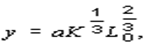
а рост с учетом взаимного влияния уравнением
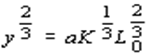, или 
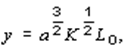
т.е. оказывается существенно более быстрым.
Для линейной модели:
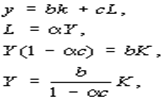
т.е. фондоотдача увеличивается.
Заключение
В заключении хотелось бы рассказать о производственной функции Кобба – Дугласа.
Возникновение теории производственных функций принято относить к 1927 г., когда появилась статья американских ученых экономиста П. Дугласа (P. Douglas) и математика Д. Кобба (D. Cobb) «Теория производства». В этой статье, была предпринята попытка, эмпирическим путем определить влияние затрачиваемого капитала и труда на объем выпускаемой продукции в обрабатывающей промышленности США.
Как уже было сказано, производственная функция отражает функциональную связь между объёмом эффективно используемых факторов производства (трудом и имущественным капиталом) и с их помощью достигаемым выпуском при существующем техническом и организационном знании.
При субституционной производственной функции производство может быть увеличено за счёт повышения количественной характеристики одного из факторов, в то время как количественная характеристика другого фактора остаётся без изменения, в другом варианте же производство остаётся без изменения при различных количественных комбинациях факторов труда и имущественного капитала.
Субстиционная производственная функция имеет, в общем следующее выражение:
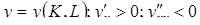
где:
K – число производственного капитала
L – число производственных трудовых часов или, другими словами, число производственных единиц гуманного капитала
На основе условно введённой субстиционности факторов производства можно сделать следующие два вывода относительно функциональной взаимосвязи данных факторов:
При прочих равных увеличение одного из факторов производства ведёт к увеличению выпуска – первая производная положительна.
Однако предельная производительность возрастающего фактора уменьшается с увеличением величины данного фактора – вторая производная отрицательна.
Уровень организационных и технических знаний отображается в соответствующих формах взаимодействий факторов. В рассматриваемом случае уровень знаний постоянен, т.е. в данных рамках предполагается отсутствие технического прогресса. Таким образом, субстиционная функция производства может быть представлена в виде следующего изображения, отражающего взаимосвязь между количеством труда и выпуском при заданном количестве имущественного капитала (рисунок 1):
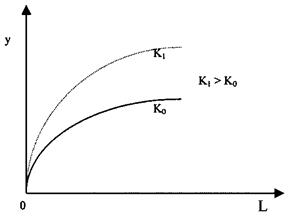
Рис. 17. Связь между производством и производственным трудом
Каждое увеличение количественного параметра имущественного капитала означает смещение кривой вверх и одновременного увеличения предельной производительности труда при заданном количестве рабочей силы, т.е. на основе вытекающего непосредственно из описанного вывода означает и более высокую величину выпуска при увеличении производственного фактора «труд»: кривая OK1 на рисунке показывает более крутой наклон по сравнению с кривой OK0 при любом числе занятых трудом.
С увеличением количественного параметра имущественного капитала увеличивается и средняя производительности труда, которая является частным от деления величины выпуска на величину затраченного труда. Однако при этом уменьшается коэффициент труда, определяющий среднее количество затраченного труда на каждую единицу выпуска и являющийся таким образом обратной величиной средней производительности труда.
Величина имущественного капитала принимается в рамках данного кратковременного анализа как экзогенно заданная, поэтому в модели и описании не учитывается технический прогресс, а также эффект увеличения производственных мощностей за счёт инвестиций.
В 1927 г. Пол Дуглас обнаружил, что если совместить графики зависимости от времени логарифмов показателей реального объема выпуска (y), капитальных затрат (К) и затрат труда (L), то расстояния от точек графика показателей выпуска до точек графиков показателей затрат труда и капитала будут составлять постоянную пропорцию. Затем он обратился к Чарльзу Коббу с просьбой найти математическую зависимость, обладающую такой особенностью, и Кобб предложил следующую субституционную функцию:
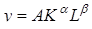
Эта функция была предложена примерно 30 годами раньше Филипом Уикстидом (Wicksteed), но они были первыми, кто использовал для ее построения эмпирические данные.
Однако при больших значениях K и L эта функция не имеет экономического смысла, т.к. выпуск все время возрастает при возрастании затрат.
Кинетическая функция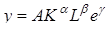 
(где g - норма технического прогресса за единицу времени) получена умножением функции Кобба-Дугласа на eg, что снимает данную проблему и делает функцию Кобба-Дугласа экономически интересной.
Эластичность выпуска продукции по капиталу и труду равна соответственно a и b, так как
,
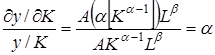и аналогичным образом легко показать, что (dy / d L)/(y /L) равно b.
Следовательно, увеличение затрат капитала на 1% приведет к росту выпуска продукции на a процентов, а увеличение затрат труда на 1% приведет к росту выпуска на b процентов. Можно предположить, что обе величины a и b находятся между нулем и единицей. Они должны быть положительными, так как увеличение затрат производственных факторов должно вызывать рост выпуска. В то же время, вероятно, они будут меньше единицы, так как разумно предположить, что уменьшение эффекта от масштаба производства приводит к более медленному росту выпуска продукции, чем затрат производственных факторов, если другие факторы остаются постоянными.
Если a и b в сумме превышают единицу, то говорят, что функция имеет возрастающий эффект от масштаба производства (это означает, что если К и L увеличиваются в некоторой пропорции, то y растет в большей пропорции). Если их сумма равна единице, то это говорит о постоянном эффекте от масштаба производства (y увеличивается в той же пропорции, что и К и L). Если их сумма меньше, чем единица, то имеет место убывающий эффект от масштаба производства (y увеличивается в меньшей пропорции, чем К и L).
В соответствии с допущением о конкурентности рынков факторов производства и b имеют дальнейшую интерпретацию как прогнозируемые доли дохода, полученного соответственно за счет капитала и труда. Если рынок труда имеет конкурентный характер, то ставка заработной платы (w) будет равна предельному продукту труда (dy / d L):
.
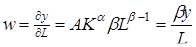Следовательно, общая сумма заработной платы (wL) будет равна b y, а доля труда в общем выпуске продукции (wL/Y) составит постоянную величину b. Аналогичным образом норма прибыли выражается через dy / dK:
,
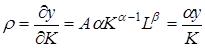и, следовательно, общая прибыль (r К) будет равна a y, а доля прибыли будет постоянной величиной a.
Существует ряд проблем по применению такой функции, особенно в тех случаях, когда она используется для экономики в целом. В частности, даже в тех случаях, когда между выпуском продукции, производственным оборудованием и трудом в производственном процессе существует технологическая зависимость, то совершенно необязательно, что подобная зависимость существует тогда, когда указанные факторы комбинируются в масштабах экономики в целом. Во-вторых, даже если такая зависимость для экономики в целом существует, то нет никаких оснований считать, что она будет иметь простую форму.
Список литературы
1. 50 лекций по микроэкономике/ Институт "Экономическая Школа", 2002.
2. Доугерти К. Введение в эконометрику: Пер. с англ. – М.: Инфра-М, 2001.
3. Институциональная экономика: курс лекций/ Кузьминов Я.И. М.: Высшая Школа Экономики, 2009.
4. Трактат по политической экономии/ Жан-Батист Сэй. Сайт "Библиотека экономической и деловой литературы".
5. Основы экономической теории. / Под ред. Камаева В.Д. - М.: Изд. МГТУ, 2006.
6. Основы экономической теории (макроэкономика): Учебное пособие./ Кравцова Г.Ф., Цветков Н.И., Островская Т.И. Хабаровск: ДВГУПС, 2001. http://www.dvgups.ru/METDOC/EKMEN/ETEOR/EK_TEOR/METOD/O_EK_TEOR/KRAV1.HTM
7. Учебник по основам экономической теории. / Под ред. В.Д.Камаева. - М.: Владос: Изд-во МГТУ им. Н. Э. Баумана, 2006.
8. Самуэльсон П. Экономика.: Пер. с англ. - М.: Прогресс, 1964.
9. Экономика предприятия: Учебник/ под ред. О.И. Волкова. – 4-е изд., перераб. и доп. – Финансы и статистика, 2000
10. Ресурс интернет - .http://slovari.yandex.ru/dict/lopatnikov/article/lop/lop-1199.htm
[1] http://slovari.yandex.ru/dict/lopatnikov/article/lop/lop-1199.htm
Дата: 2019-05-29, просмотров: 206.
