Использование аппарата производственных функций дает возможность решения задачи об оптимальном использовании средств, предназначенных для приобретения производственных факторов.

Предположим, что факторы ( x ₁ , ..., x _N ) могут быть закуплены по ценам ( p ₁ , ..., p _N ), а объем имеющихся средств для приобретения составляет b (руб.). Тогда соотношение, описывающее множество допустимых наборов факторов, имеет вид

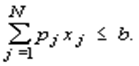
Граничная линия этого множества, соответствующая полному использованию имеющихся средств, т.е.

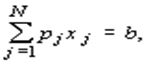
называется изокостой, поскольку ей отвечают наборы, имеющие одинаковую стоимость b . Задача об оптимальном использовании средств формулируется так: требуется найти набор факторов, который дает наибольший выпуск продукции при ограниченных финансовых средствах b . Таким образом, требуется найти решение задачи:

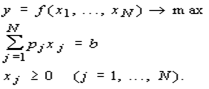
Искомое решение находится из системы уравнений:

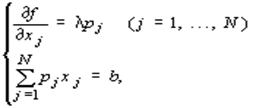
где l множитель Лагранжа.

В частности, если число факторов N = 2, задача допускает наглядную геометрическую интерпретацию (рис. 7).

Рис. 7. Оптимальная комбинация ресурсов

Здесь отрезок АВ есть изокоста , кривая R изокванта, касающаяся изокосты в точке D , которая и соответствует оптимальному набору факторов ( ).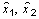

Полезно привести полное решение поставленной задачи для случая двух факторов, т.е. N = 2.

Пусть x ₁ = K капитал (основные фонды),

x ₂ = L труд (рабочая сила);

производственная функция

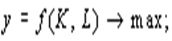
условие ограниченности ресурса

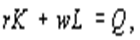
где r цена использования машин и оборудования (т.е. услуг капитала), равная норме банковского процента; w ставка оплаты труда.

Условия оптимальности имеют вид

а)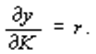

Это условие означает, что объем используемого капитала должен быть принят на том уровне, когда маргинальная фондоотдача ( y / K ) равна норме процента; дальнейшее увеличение капитала приведет к снижению его эффективности;

б)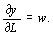

Это условие требует, чтобы количество занятой рабочей силы было взято на уровне, когда маргинальная производительность труда ( y / L ) равна ставке заработной платы, так как дальнейшее увеличение количества занятых приводит к убыткам (точка на рис. 8).

Рис. 8. Оптимальное количество занятых

Здесь угловой коэффициент касательной в точке А равен w .

Для ПФ типа КоббаДугласа задача имеет вид

найти

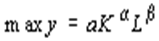
при условии

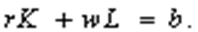
Получим следующее решение

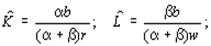
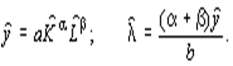
Множитель 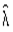характеризует здесь предельную продуктивность финансовых средств, т.е. показывает, на какую величину D y изменится максимальный выпуск продукции 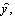если объем средств b увеличится на малую единицу.

Заметим, что сумма эластичностей капитала (иa ) характеризует так называемый удельный выпуск (отдачу) приbтруда ( изменении масштаба производства, т.е. когда расход ресурсов ( K и L ) увеличивается в одинаковое число раз. Если a + b > 1, то отдача возрастает, если a + b = 1, то отдача постоянная, если a + b < 1, то отдача убывает, а производственная функция является выпуклой вверх.