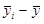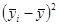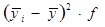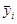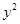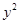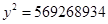| Исходные данные | Расчетные значения | |||||
| Группы банков по объему выданных ссуд коммер. банками, млн.р | Число банков в группе f | Середина интервала x |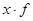 
| 
| 
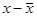
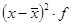
| Накопленные частоты |
| 9054-34254 | 7 | 21654 | 151578 | -37800 | 10001880000 | 7 |
| 34254-59454 | 11 | 46854 | 515394 | -12600 | 1746360000 | 18 |
| 59454-84654 | 5 | 72054 | 360270 | 12600 | 793800000 | 23 |
| 84654-109854 | 4 | 97254 | 389016 | 37800 | 5715360000 | 27 |
| 109854-135054 | 3 | 122454 | 367362 | 63000 | 11907000000 | 30 |
| Итого | 30 | - | 1783620 | - | 30164400000 | - |
1. Найдем среднюю арифметическую.
Для расчета, в качестве значений признаков в группах примем середины этих интервалов (х), так как значения осредняемого признака заданы в виде интервалов. Рассчитаем и подставим полученные значения в таблицу.
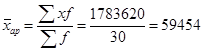млн.руб. (2)
Итак, средний объем выданных ссуд коммерческими банками составляет 59454 млн.руб.
2. Найдем среднее квадратичное отклонение по формуле:
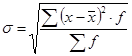(3)
Для этого сделаем промежуточные расчеты и подставим их в таблицу.
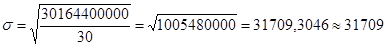млн.руб.
3. Найдем коэффициент вариации по формуле:
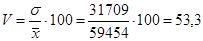% (4)
4. Найдем моду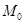 
по формуле:
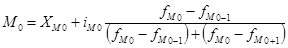, (5)
где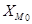 
- нижняя граница модального интервала;
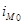- модальный интервал;
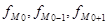- частоты в модальном, предыдущем и следующим за модальным интервалах (соответственно).
Модальный ряд определяется по наибольшей частоте. Из таблицы видно, что данным интервалом является (34254 – 59454 млн.руб.).
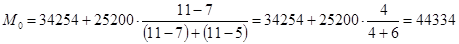млн.руб.
5. Найдем медиану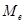 
по формуле:
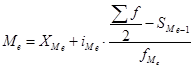, (6)
где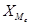 
- нижняя граница медианного интервала;
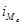- медианный интервал;
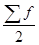- половина от общего числа наблюдений;
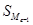- сумма наблюдений, накопленная до начала медианного интервала;
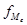- число наблюдений в медианном интервале.
Прежде всего, найдем медианный интервал. Таким интервалом будет (34254 – 59454 млн.руб.).
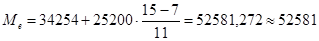млн.руб.
Выводы:
Так как V>33%, то это говорит о значительной колеблемости признака, о не типичности средней величины, об неоднородности совокупности.
Так как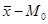 
> 0, т.е. (59454 - 44334) > 0, то наблюдается правосторонняя ассиметрия.
Задание 2
По исходным данным:
1. Установите наличие и характер связи между объемом выданных ссуд и прибылью коммерческих банков методом аналитической группировки, образовав, пять групп с равными интервалами по объему выданных ссуд коммерческими банками.
2. Измерьте тесноту корреляционной связи между названными признаками с использованием коэффициентов детерминации и эмпирического корреляционного отношения.
Сделайте выводы по результатам выполнения задания.
РЕШЕНИЕ
Для построения корреляционной таблицы необходимо знать величины и границы интервалов по двум признакам X и Y. Для факторного признака Х – Объем выданных ссуд эти величины известны из задания 1. Определяем величину интервала для результативного признака Y – Прибыль коммерческих банков при n = 5, у max = 9003 млн руб., у min = 453 млн руб.:
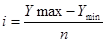, (7)
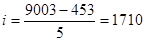млн.руб. - величина интервала
Таблица 5 Распределение банков по объему выданных ссуд коммерческих банков
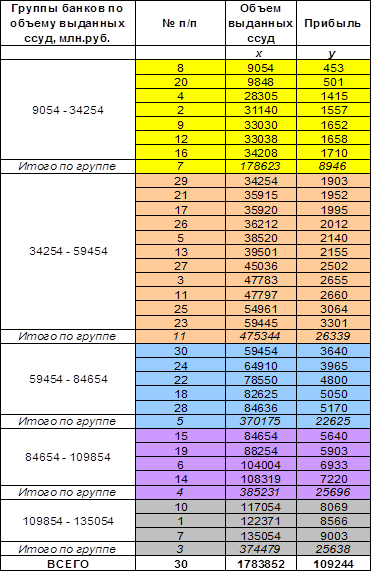
На основании таблицы 5 построим итоговую таблицу 6 аналитической группировки.
Таблица 6 Зависимость прибыли от объема выданных ссуд коммерческими банками
| Номер группы | Группы банков по объему выданных ссуд, млн.руб. | Число банков в группе | Прибыль, млн руб. | |
| Всего | В среднем на один банк | |||
|
|
| f | y | |
| 1 | 9054 - 34254 | 7 | 8946 | 1278 |
| 2 | 34254-59454 | 11 | 26339 | 2395 |
| 3 | 59454-84654 | 5 | 22625 | 4525 |
| 4 | 84654-109854 | 4 | 25696 | 6424 |
| 5 | 109854-135054 | 3 | 25638 | 8546 |
ИТОГО
30
109244
3642
Общую среднюю результативного признака по совокупности в целом можно определить следующим способом:
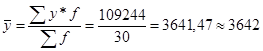млн.руб. (8)
Анализ таблицы 6 показывает, что с ростом объема выданных ссуд от группы к группе возрастает и средняя прибыль банка. Следовательно, между объемом выданных ссуд и прибылью коммерческих банков существует прямая корреляционная взаимосвязь.
Опираясь на исходные данные таблицы 3 и на данные таблицы 6, измерим тесноту корреляционной связи с использованием коэффициента детерминации и эмпирического корреляционного отношения.
РЕШЕНИЕ
Коэффициент детерминации:
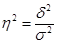(9)
Вычислим межгрупповую дисперсию по формуле:
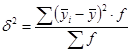(10)
Расчеты произведем в таблице.
Таблица 7
| Группы банков по объему выданных ссуд, млн.руб. | Число банков в группе | Прибыль, млн.руб. | Расчет показателей | ||
| В среднем на один банк |
|
|
| ||
|
| f |
|
|
|
|
| 9054 - 34254 | 7 | 1278,000 | -2363,467 | 5585974,684 | 39101822,791 |
| 34254-59454 | 11 | 2394,455 | -1247,012 | 1555039,230 | 17105431,535 |
| 59454-84654 | 5 | 4525,000 | 883,533 | 780631,151 | 3903155,756 |
| 84654-109854 | 4 | 6424,000 | 2782,533 | 7742491,751 | 30969967,004 |
| 109854-135054 | 3 | 8546,000 | 4904,533 | 24054447,218 | 72163341,653 |
ИТОГО
30
3641,467
-
-
163243718,739
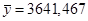млн.руб.
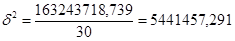
Теперь вычислим общую дисперсию на основе несгруппированных данных из таблицы 3 по формуле:
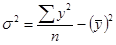(11)
Для этого в начале возведем данные по прибыли в квадрат:
Таблица 8
| № п/п | Прибыль, млн.руб. |
| № п/п | Прибыль, млн.руб. |
|
| y |
| y |
| ||
| 1 | 8566 | 73376356 | 16 | 1710 | 2924100 |
| 2 | 1557 | 2424249 | 17 | 1995 | 3980025 |
| 3 | 2655 | 7049025 | 18 | 5050 | 25502500 |
| 4 | 1415 | 2002225 | 19 | 5903 | 34845409 |
| 5 | 2140 | 4579600 | 20 | 501 | 251001 |
| 6 | 6933 | 48066489 | 21 | 1952 | 3810304 |
| 7 | 9003 | 81054009 | 22 | 4800 | 23040000 |
| 8 | 453 | 205209 | 23 | 3301 | 10896601 |
| 9 | 1652 | 2729104 | 24 | 3965 | 15721225 |
| 10 | 8069 | 65108761 | 25 | 3064 | 9388096 |
| 11 | 2660 | 7075600 | 26 | 2012 | 4048144 |
| 12 | 1658 | 2748964 | 27 | 2502 | 6260004 |
| 13 | 2155 | 4644025 | 28 | 5170 | 26728900 |
| 14 | 7220 | 52128400 | 29 | 1903 | 3621409 |
| 15 | 5640 | 31809600 | 30 | 3640 | 13249600 |
| ИТОГО | 385001616 | ИТОГО | 184267318 | ||
|
ВСЕГО |
| ||||
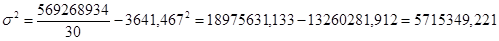
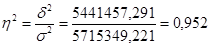или 95,2 %.
Эмпирическое корреляционное отношение находим по формуле:
Для изучения связи между явлениями и их признаками строим групповую корреляционную таблицу . По данным таблицы 5 определяем существует ли зависимость между объемами выданных ссуд (факторный признак X) и размером прибыли коммерческих банков (результативный признак Y). Построим корреляционную таблицу, образовав пять групп по факторному и результативному признакам.
Таблица 9
Групповая корреляционная таблица
| Объем выданных ссуд | Размер прибыли, млн. руб. | |||||
| 453-2155 | 2155-3640 | 3640-5170 | 5170-7220 | 7220-9003 | Итого | |
| 9054-34254 | 7 | 7 | ||||
| 34254-59454 | 5 | 6 | 11 | |||
| 59454-84654 | 5 | 5 | ||||
| 84654-109854 | 4 | 4 | ||||
| 109854-135054 | 3 | 3 | ||||
| Итого | 12 | 6 | 5 | 4 | 3 | 30 |
Вывод: Коэффициент детерминации говорит о том, что вариация прибыли на 95,2% зависит от вариации объема выданных ссуд и на 4,8% от прочих признаков.
Эмпирическое корреляционное отношение по своей величине близко к единице, что свидетельствует о весьма тесной взаимосвязи между объемом выданных ссуд и прибыли коммерческих банков.
Задание 3
По результатам выполнения задания 1 с вероятностью 0,954 определите:
1. Ошибку выборки среднего объема выданных ссуд и границы, в которых будет находиться этот показатель в генеральной совокупности.
2. Ошибку выборки доли коммерческих банков, имеющих объем выданных ссуд 59 454 млн руб. и более и границы, в которых будет находиться генеральная доля.
РЕШЕНИЕ:
1) По результатам выполнения задания 1 и с учетом, что выборка 1,5%-механическая, определим с вероятностью 0,954 ошибку выборки среднего объема выданных ссуд и границы, в которых будет находиться показатель в генеральной совокупности:
Имеются данные: n = 30; p = 0,954; t = 2; n/N = 0,015;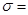 
31709
Так как выборка механическая, то используем следующую формулу:
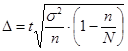
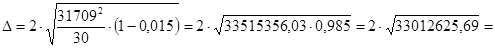
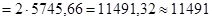млн.руб.
Пределы для средней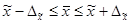 
59454-11491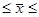 
59454+11491
47963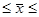 
70945 (млн.руб.)
б) По результатам выполнения задания 1 имеем данные:
n = 30; m = 12; W = m/n = 12/30 = 0,4; n/N = 0,015.
Ошибку выборки доли коммерческих банков, имеющих объем выданных ссуд 59454 млн.р. и более найдем по следующей формуле:
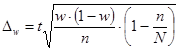
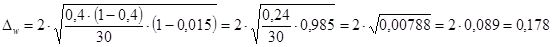
Пределы для доли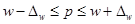 
0,4 – 0,178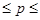 
0,4+0,178; 0,222 ≤ р ≤ 0,578 или 22,2≤ р ≤57,8 (%)
Вывод: Таким образом, с вероятностью 0,954 можно ожидать, что средний объем выданных ссуд в генеральной совокупности будет не менее 47963 и не более 70945.
С вероятностью 0,954 можно утверждать, что доля коммерческих банков, имеющих объем выданных ссуд 59454 млн.руб. и более, по всей совокупности составит от 22,2 до 57,8 %.
Задание 4
Имеются следующие данные о краткосрочном кредитовании предпринимателей региона коммерческим банком, млн руб.:
Таблица 6
| Отрасли | Средняя длительность пользования кредитом, дней | Структура однодневного оборота кредита по погашению, % | ||
| Базисный год | Отчетный год | Базисный год | Отчетный год | |
| Промышленность | 38 | 40 | 16 | 15 |
| Торговля | 12 | 10 | 58 | 60 |
| Общественное питание | 15 | 15 | 26 | 25 |
Определите:
1. Индексы средней длительности пользования кредитом переменного состава, постоянного состава и структурных сдвигов.
2. Абсолютное изменение средней длительности пользования кредитом за счет изменения длительности пользования кредитом по отраслям и изменения структуры однодневного кредита.
Сделайте выводы.
РЕШЕНИЕ:
Для того, чтобы рассчитать индексы переменного, постоянного состава и структурных сдвигов рассчитаем необходимые значения и приведем их в таблицу.
Таблица 7
Дата: 2019-05-29, просмотров: 263.
