Прикладное значение механики сплошных сред заключается в том, что она создает фундамент для физико-математического моделирования процессов взаимодействия деформируемых тел и сред. С помощью формулируемых в механике сплошных сред уравнений и соотношений удается составить замкнутую систему уравнений, решение которых позволяет исследовать поведение деформируемых сред и получать информацию о параметрах их движения и состояния. В настоящее время именно физико-математическое моделирование с позиций механики сплошных сред является наиболее мощным инструментом расчетно-теоретического исследования функционирования различных технических объектов, как существующих, так и проектируемых. В качестве примеров прикладных задач, необходимость решения которых возникает при изучении функционирования газодинамических импульсных устройств, можно указать задачи обтекания тел вращения воздушным потоком (рис. 2, а), проникания тел вращения в плотные и прочные среды (рис. 2, б, в), метания металлических облицовок продуктами детонации взрывчатого вещества (рис. 2, г), схлопывания конических металлических облицовок под действием приложенного давления с формированием кумулятивной струи (рис. 2, д) и т.п.

Однако решению задачи обязательно предшествует весьма важный этап формализации рассматриваемого физического процесса: его описание в виде соответствующей системы

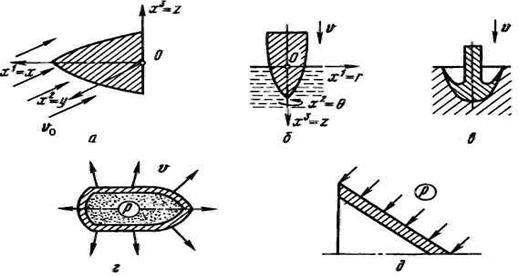
Рисунок 2

уравнений, соотношений и определенных условий, т.е. решению задачи предшествует так называемая постановка задачи или же формулировка физико-математической модели изучаемого процесса взаимодействия деформируемых тел или сред. Далее приведем общие принципы постановки задач механики сплошных сред с различными физико-механическими свойствами и последовательно проанализируем особенности постановки задач механики идеальной и вязкой жидкостей, упругой и упругопластической сред. При этом основное внимание уделим этапам составления замкнутой системы исходных уравнений, получению системы разрешающих уравнений и различных частных ее видов, особенностям задания граничных условий. Постановку задачи механики упругопластической среды рассмотрим в полном объеме на примере процесса проникания металлического тела в металлическую преграду.

Постановка задачи механики сплошных сред заключается в составлении такой замкнутой системы уравнений и соотношений, которая бы описывала движения и состояние деформируемых сред с учетом их физико–механических свойств, действия внешних сил, тепловых и других факторов и позволяла определять зависимости характеризующих движение и состояние физических величин от координат и времени 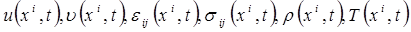и т.п.

Постановка любой задачи механики сплошных сред включает следующие пять этапов:

— выбор системы отсчета и системы координат, по отношению к которым будет описываться движение материального континуума;

— выбор моделей сплошных сред для участвующих в исследуемом процессе реальных деформируемых сред;

— составление системы исходных уравнений для выбранных моделей и исследуемого процесса;

— выбор основных неизвестных характеристических функций и переход к так называемой системе разрешающих уравнений;

— формулировка начальных и граничных условий для решаемой задачи.

2.2.1 Выбор системы отсчета и системы координат. В большинстве случаев при постановке прикладных задач выбираются инерциальные системы отсчета, неподвижные относительно земной поверхности. Как известно, выбор такой системы отсчета позволяет использовать при математическом описании движения законы механики Ньютона, в частности уравнение движения (2.1.2), являющееся выражением второго закона Ньютона применительно к сплошным деформируемым средам. Например, для показанного (на рис. 2, б) случая проникания тела вращения в плотную среду в качестве точки отсчета удобно принять неподвижную относительно Земли точку 0 начала взаимодействия проникающего тела с плотной средой. В некоторых более редких случаях допустимо и более удобно использование неинерциальных систем отсчета. Например, при решении задачи расчета характеристик напряженно-деформированного состояния проникающего тела — оболочки вращения — и оценке его прочности удобнее связать систему отсчета с самим тормозящимся в процессе проникания телом. Однако в этом случае в соответствии с принципом Даламбера следует включить в число внешних сил объемные силы инерции, для чего необходимо предварительное определение ускорения проникающего тела.

Выбор конкретного вида системы координат 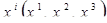 произволен и определяется, прежде всего, соображениями удобства и простоты математического описания движения. Так, при решении задачи пространственного обтекания тела воздушной средой (см. рис. 2, а) все параметры движения и состояния газа зависят от трех координат и времени (трехмерная нестационарная задача). В этом случае целесообразно выбрать наиболее простую систему координат — декартову прямоугольную систему координат (х1 = х, х2 = у, х3 = z). При проникании тела вращения в преграду по нормали к ней (см. рис. 2, б) очевидна осевая симметрия движения, в этом случае наиболее целесообразен выбор цилиндрической системы координат (х1 = r, х2 = 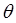, х3 = z), в которой вектор скорости движения частиц имеет лишь две отличные от нуля компоненты υT и υZ а также отсутствует зависимость параметров движения и состояния деформируемой среды от угловой координаты  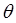(двумерная осесимметричная нестационарная задача). В еще более геометрически простом случае взрыва сферического заряда, инициируемого в центре, движение обладает точечной симметрией, поэтому наиболее удобно принять для описания движения сферическую систему координат (х1 = r, х2 = 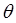, х3 = φ), которая обеспечивает зависимость параметров движения и состояния среды лишь от одной радиальной координаты r и времени t (одномерная нестационарная задача с центральной симметрией).

2.2.2 Выбор модели сплошной среды и составление системы исходных уравнений. Выбор модели сплошной среды для участвующей в исследуемом процессе реальной деформируемой среды базируется на анализе особенностей поведения этой среды в отношении сопротивления деформированию, на выделении основных факторов и игнорировании второстепенных. Этап выбора модели заканчивается определением конкретного вида физических соотношений (2.1.7), ближе всего соответствующих особенностям физико-механического поведения реальной деформируемой среды.

Например, при решении прикладной задачи проникания тела вращения в воду с относительно небольшой начальной скоростью взаимодействия 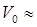100 м/с в качестве модели реальной деформируемой среды (воды) вполне допустимо принять модель идеальной жидкости. Действительно, реальные жидкости обладают свойством сжимаемости и вязкости и в то же время не оказывают сопротивления непосредственно изменению формы своих частиц. При малых скоростях деформации, соответствующих малым скоростям взаимодействия, можно также пренебречь влиянием вязкости и вообще не учитывать появление касательных напряжений, используя для описания физико-механического поведения физические соотношения 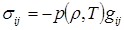, присущие модели идеальной среды.

Следует отметить, что достаточно часто выбор модели сплошной среды применительно к процессам, происходящим в экстремальных условиях (например, к взрывным и ударным), осуществляется итерационным путем, так как заранее трудно предсказать, какие именно физико-механические свойства реальных сред будут определяющими, а какими можно пренебречь. В таких случаях последовательно используют все более сложные модели, а критерием удовлетворительности выбораявляется соответствие получаемых расчетным путем результатов, имеющимся экспериментальным данным.

Система исходных уравнений – это замкнутая система уравнений и соотношений которая полностью описывает движение и состояние деформируемых сред с учетом их физико-механических свойств. В самом общем виде система исходных уравнений имеет следующий вид [53]:

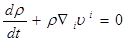, (2.2.1)

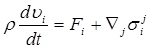, (2.2.2)

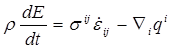, (2.2.3)

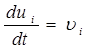, (2.2.4)

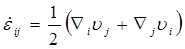, (2.2.5)

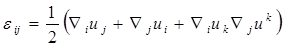, (2.2.6)

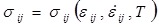. (2.2.7)

Система исходных уравнений в обязательном порядке включает основные общие для всех сплошных сред дифференциальные уравнения механики, выражающие фундаментальные законы сохранения массы (2.2.1), импульса (2.2.2), энергии (2.2.3), а также общие для всех сред кинематические соотношения (2.2.4) и (2.2.5) и геометрические соотношения (2.2.6). Индивидуальные особенности рассматриваемой деформируемой среды в отношении оказания сопротивления деформированию учитываются физическими соотношениями (2.2.7), обязательно включаемыми в систему исходных уравнений согласно выбранной модели сплошной среды.

В зависимости от конкретного вида физических соотношений (2.2.7) и от характера процесса деформирования среды в систему исходных уравнений для обеспечения ее замкнутости могут быть включены дополнительные уравнения и соотношения. Например, при отсутствии влияния температуры на физико-механическое поведение рассматриваемой среды физические соотношения имеют вид 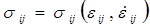 и для адиабатического процесса  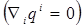система уравнений (2.2.1)—(2.2.7) является замкнутой и содержит 26 уравнений и соотношении и такое же количество искомых характеристических функций (см. раздел 2.1). Напротив, в случаях зависимости компонент тензора напряжений от температуры или же при учете теплообмена между частицами сплошной среды и необходимости определения температурного поля в систему исходных уравнений необходимо включать дополнительные соотношения, учитывающие закон теплопроводности Фурье 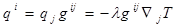, где λ — коэффициент теплопроводности) и взаимосвязь между удельной внутренней энергией и температурой (Е = Е(ρ,Т)).

В ряде случаев система исходных уравнений может быть и более узкой, нежели представленная выше система (2.2.1)—(2.2.7). Например, при постановке задачи механики идеальной жидкости, для которой компоненты тензора напряжений не зависят напрямую от компонент тензора деформаций (зависимость напряжений от деформаций имеет косвенный характер через плотность, взаимосвязанную с объемной деформацией, не требуется включения в систему исходных уравнений кинематических соотношений (2.2.4) и геометрических соотношений (2.2.6). Однако в любом случае следует обеспечивать замкнутость системы исходных уравнений с равенством количества уравнений числу неизвестных характеристических функций, описывающих движение и состояние сплошной среды. Это является необходимым условием для последующего нахождения единственного решения задачи.

2.2.3 Начальные и граничные условия. Неотъемлемым и важнейшим элементом постановки любой задачи механики сплошных сред является формулировка начальных и граничных условий. Их значение определяется тем, что та или иная система разрешающих уравнений описывает целый класс движений соответствующей деформируемой среды, и лишь задание отвечающих исследуемому процессу начальных и граничных условий позволяет выделить из этого класса представляющий интерес частный случай, соответствующий решаемой практической задаче.

Начальные условия — это условия, которыми задаются значения искомых характеристических функций в момент начала рассмотрения исследуемого процесса. Количество задаваемых начальных условий определяется количеством основных неизвестных функций, входящих в систему разрешающих уравнений, а также порядком входящей в эту систему высшей производной по времени. Например, адиабатическое движение идеальной жидкости или идеального газа описывается системой шести уравнений с шестью основными неизвестными — тремя компонентами вектора скорости 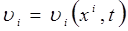,давлением 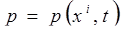,плотностью 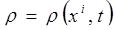и удельной внутренней энергией 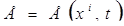, при этом порядок производных этих физических величин по времени не превышает первый порядок. Соответственно этому в качестве начальных условий должны быть заданы начальные поля этих шести физических величин: при t =0 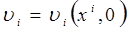, , 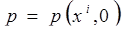, 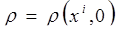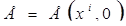. В некоторых случаях (например, в динамической теории упругости) в качестве основных неизвестных в системе разрешающих уравнений используются не компоненты  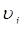вектора скорости, а компоненты 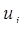вектора перемещения, а уравнение движения содержит производные второго порядка компонент перемещения 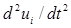, что требует задания двух начальных условий для искомой функции 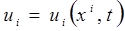: при t = 0

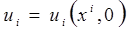 и .

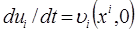Более сложным и разнообразным образом при постановке задач механики сплошных сред задаются граничные условия. Граничные условия — это условия, которыми задаются значения искомых функций (или их производных по координатам и времени) на поверхности S области, занимаемой деформируемой средой. Различают граничные условия нескольких типов: кинематические, динамические, смешанные и температурные.

Кинематические граничные условия соответствуют случаю, когда на поверхности S тела (или ее части) задаются перемещения 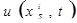 или скорости  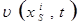где 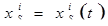 — координаты точек поверхности S, изменяющиеся в общем случае в зависимости от времени.

Динамические граничные условия (или граничные условия в напряжениях) задаются, когда на поверхности S действуют поверхностные силы р. Как следует из теории напряжений, в этом случае на любой элементарной площадке поверхности с единичным вектором нормали п вектор удельных поверхностных сил рп принудительно задает вектор полного напряжения σп = рn, действующий в сплошной среде в точке на данном участке поверхности, что приводит к взаимосвязи тензора напряжений (σ) в этой точке с поверхностной силой и ориентацией вектора п соответствующего участка поверхности: (σ) · п = рп или .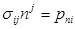

Смешанные граничные условия соответствуют случаю, когда на поверхности S задаются значения и кинематических, динамических величин или устанавливаются взаимосвязи между ними.

Температурные граничные условия подразделяются на несколько групп (родов). Граничные условия первого рода задают на поверхности S деформируемой среды определенные значения температуры Т. Граничные условия второго рода задают на границе вектор теплового потока q, что с учетом закона теплопроводности Фурье q = — λ grad T, по существу, накладывает ограничения на характер температурного распределения в окрестности граничной точки 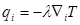. Граничные условия третьего рода устанавливают зависимость между вектором теплового потока q, направленным к данной среде со стороны окружающей среды, и температурным перепадом между этими средами и т.д.

Следует отметить, что постановка и решение большинства задач физики быстропротекающих процессов, как правило, осуществляются в адиабатическом приближении, поэтому температурные граничные условия используются достаточно редко, в основном в различных сочетаниях применяются кинематические, динамические и смешанные граничные условия. Рассмотрим возможные варианты задания граничных условий на частном примере.

На рис. 3 схематично представлен процесс взаимодействия при проникании деформируемого тела I в деформируемую преграду II. Тело I ограничено поверхностями S1 и S5, а тело II — поверхностями S2, S3, S4, S5. По -
верхность S5 является границей раздела взаимодействующих деформируемых тел. Будем полагать, что движение тела I до начала взаимодействия, а также в его процессе происходит в жидкости, создающей определенное гидростатическое давление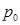

Рисунок 3

и задающей внешние по отношению к обоим телам поверхностные силы рп = — р 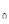п= — р 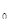ni ri, действующие на любой из элементарных площадок поверхностей S1 тела I и S2 преграды II, граничащих с жидкостью. Будем также считать, что поверхность Sз преграды жестко закреплена, а поверхность S4 свободна от действия поверхностных сил (рп = 0).

Для приведенного примера на различных поверхностях, ограничивающих деформируемые среды I и II, должны задаваться граничные условия всех трех основных типов. Очевидно, что на жестко закрепленной поверхности Sз следует задать кинематические граничные условия υ(S3) = υ( 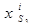, t) = 0. Граничные условия на поверхностях S1 и S2 однотипны и относятся к динамическим условиям, накладывающим ограничения на компоненты тензора напряжений в граничных точках соответствующих тел:  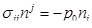или 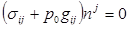Компоненты тензора напряжений на поверхности S4 преграды также не могут быть произвольными, а взаимосвязаны с ориентацией ее элементарных площадок как .

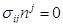Граничные условия на границе раздела (поверхность S5) взаимодействующих деформируемых сред являются наиболее сложными и относятся к условиям смешанного типа, включающим, в свою очередь, кинематическую и динамическую части (см. рис. 3). Кинематическая часть смешанных граничных условий накладывает ограничения на скорости движения индивидуальных точек обеих сред, находящихся в контакте в каждой пространственной точке поверхности S5. Возможны два варианта задания этих ограничений, проиллюстрированные на рис. 4, а и б. По наиболее простому первому варианту предполагается, что скорости движения любых двух находящихся в контакте индивидуальных точек одинаковы (υ = υ ) — это так называемое условие "прилипания", или условие "сварки" (см. рис. 4, а). Более сложным и в то же время более адекватным для рассматриваемого процесса является задание условия "непроницаемости", или условия "непротекания" (υ · n= υ · n; см. рис. 4, б), которое соответствует экспериментально подтверждающемуся факту: взаимодействующие деформируемые среды не могут проникать

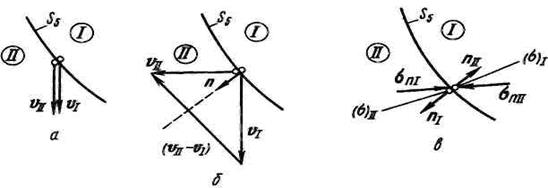
Рисунок 4

друг в друга или отставать друг от друга, а могут проскальзывать одна относительно другой со скоростью υ – υ , направленной по касательной к границе раздела ((υI – υII) · n = 0). Динамическая часть смешанных граничных условий на границе раздела двух сред формулируется на основе третьего закона Ньютона с использованием соотношений теории напряжений (рис. 4, в). Так, в каждой из двух находящихся в контакте индивидуальных частиц деформируемых сред I и II реализуется свое напряженное состояние, характеризуемое тензорами напряжений (σ)I и (σ) II.При этом в среде I на каждой элементарной площадке границы раздела с единичным вектором нормали nII, внешней по отношению к данной среде, действует вектор полного напряжения σnI = (σ)·nI. В среде II на той же площадке, но с единичным вектором нормали nII , внешней по отношению к этой среде, действует вектор полного напряжения σnII =(σ)II · пII. С учетом взаимности действия и противодействия σnI = - σ n II , а также очевидного условия nI = —nII = n устанавливается взаимосвязь между тензорами напряжений в обеих взаимодействующих средах на границе их раздела: (σ)I · п = (σ) II ·п или же (σijI - σijII ) nj = 0.Возможные варианты задания граничных условий не исчерпываются рассмотренным частным примером. Вариантов задания начальных и граничных условий столь же много, сколь много существует в природе и технике процессов взаимодействия деформируемых тел или сред. Они определяются особенностями решаемой практической задачи и задаются в соответствии с приведенными выше общими принципами.