Термоупругая деформация тела, возникающая от нестационарных механических и тепловых воздействий, сопровождается обратным эффектом — изменением его температурного поля. Задача термоупругости, в которой учитывается указанный эффект, называется связанной динамической задачей термоупругости, или связанной задачей термоупругости.
Эффекты связанности. Законы термодинамики гласят, что изменение деформаций упругого тела сопровождается изменением его температуры, при котором возникает теплопоток, обусловливающий увеличение энтропии термодинамической системы и, следовательно, термоупругое рассеяние энергии.
В металлических телах эффект связанности поля деформации и температурного поля обычно мало влияет на термическое возмущение и распределение тепловых напряжений. Но это не значит, что подобное положение сохранится и для новых материалов, обладающих большим параметром связанности.
При учете эффекта связанности устанавливаются новые качественные особенности распространения упругих волн, которые под влиянием тепловых эффектов распространяются с затуханием и дисперсией. В частности, существенно различаются решение динамической задачи термоупругости о тепловом ударе на поверхности полупространства без учета связи полей деформации и температуры и решение с учетом этой связи; в случае «несвязанного» решения разрыв напряжения αх остается неизменным, тогда как при «связанном» он с течением времени быстро уменьшается.
В работе, связанная задача термоупругости рассматривается при малом термическом возмущении, т. е. при 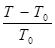 << 1
<< 1
В этом случае связанная задача становится линейной и при формулировке ее в перемещениях сводится к решению системы уравнений (1.2.12) и (1.2.13). Представления общих решений этой системы обобщают представления общих решений уравнения (1.3.30), описывающего динамическую задачу термоупругости. Известные представления решения уравнений классической теории упругости Б. Г. Галеркина и П. Ф. Папковича обобщаются на случай связанной задачи термоупругости. Применение прямых методов для решения связанных задач термоупругости в общем случае встречает большие математические затруднения; перспективной является разработка приближенных методов решения связанных задач термоупругости на основе вариационных принципов, аналогичных таковым для статических и квазистатических задач термоупругости.
Представления общего решения. Связанная задача термоупругости при малом термическом возмущении описывается системой уравнений (1.2.12) и (1.2.13) при начальных и граничных условиях.
При объемной силе
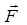 = grad П + rot
= grad П + rot 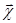 (1.3.1)
(1.3.1)
известно следующее представление общего решения уравнений (1.2.12) и (1.2.13):
и =grad 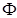 + rot
+ rot 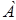 (1.3.2)
(1.3.2)
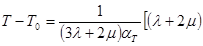 □
□ 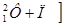 ,
,
в котором скалярная Ф и векторная 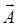 функции удовлетворяют уравнениям
функции удовлетворяют уравнениям
□ 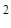
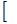 □
□ 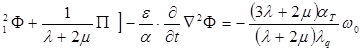 ; ( 1.3.3)
; ( 1.3.3)
□ 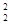
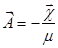 (1.3.4) где
(1.3.4) где
□ 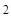 =
= 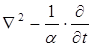 □
□  =
= 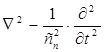 (n= 1,2); (1.3.5)
(n= 1,2); (1.3.5)
ε — параметр связанности, имеющий значение;
с1 и с2 — скорость распространения упругой волны соответственно расширения и искажения (см. выражения (1.3.6)). При ε = 0 и П = 0 уравнение (1.3.3) на основании уравнения (1.3.31) переходит в (1.3.7)
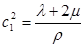 ,
, 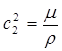 (1.3.6)
(1.3.6)
□ 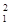
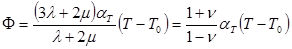 (1.3.7)
(1.3.7)
а при 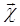 = 0 уравнение (1.3.4) переходит в уравнение (1.3.8) динамической задачи термоупругости.
= 0 уравнение (1.3.4) переходит в уравнение (1.3.8) динамической задачи термоупругости.
□ 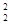
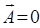 (1.3.8)
(1.3.8)
Найдено также обобщение известного представления решения уравнений классической теории упругости Б. Г. Галеркина [52] (на случай связанной задачи термоупругости):
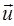 = grad
= grad 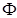 +
+ 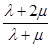 □
□ 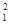
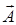 - grad div
- grad div 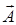 (1.3.9)
(1.3.9)
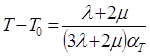 □
□ 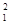
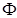
где функция 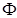 и
и 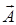 удовлетворяют уравнениям
удовлетворяют уравнениям
□  □
□ 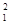
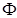
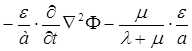 □
□ 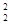
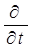 div
div 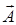
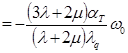 (1.3.10)
(1.3.10)
□ 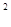 □
□ 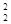
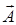
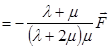 (1.3.11)
(1.3.11)
Как и в динамической задаче термоупругости, представление (1.3.9) при отсутствии объемных сил можно преобразовать к представлению (1.3.2). Действительно, если в представление (1.3.9) и уравнение (1.3.10) внести выражения
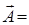
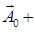
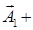
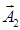 ,
,
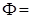
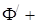 div
div 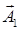 (1.3.12)
(1.3.12)
в которых 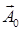 — частное решение неоднородного уравнения (1.3.11),
— частное решение неоднородного уравнения (1.3.11), 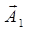 и
и 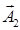 - решения уравнений
- решения уравнений
□ 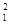
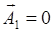 , □
, □ 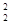
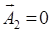 (1.3.13)
(1.3.13)
Ф'— новая скалярная функция, то форма их не изменится, но вместо Ф и  в представлении (1.3.9) возникают Ф' и
в представлении (1.3.9) возникают Ф' и 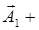
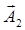 , а в уравнении (1.3.10) Ф' и
, а в уравнении (1.3.10) Ф' и 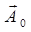 . На основании второго уравнения (1.3.13) и тождества
. На основании второго уравнения (1.3.13) и тождества
grad div 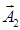 =
= 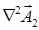 + rot rot
+ rot rot 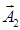
при подстановке — rot 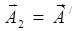 такое представления при
такое представления при 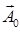 = 0, П = 0, X = 0 (отсутствие объемных сил) переходит в представление (1.3.2).
= 0, П = 0, X = 0 (отсутствие объемных сил) переходит в представление (1.3.2).
Вводя в представление (1.3.9) и в уравнения (1.3.10) и (1.3.11) новые функции
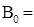 div
div 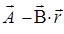 ,
, 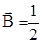 □
□ 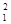
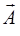 (1.3.14)
(1.3.14)
где r — радиус-вектор, получаем обобщение известного представления П. Ф Папковича на случай связанной задачи термоупругости (1.3.14)
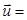 grad
grad  grad
grad 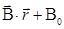 ; (1.3.15)
; (1.3.15)
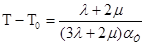 □
□ 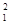
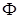 ,
,
в котором функция Ф,  , В0 удовлетворяют уравнениям
, В0 удовлетворяют уравнениям
□ 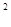 □
□ 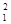
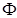
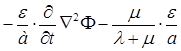 □
□ 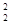
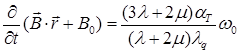 (1.3.16)
(1.3.16)
□ 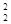
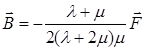 ,
, 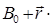 □
□ 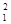
 (1.3.17)
(1.3.17)
В случае распространения безвихревой волны (волны расширения) и отсутствия объемных сил и источников тепла 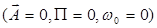 представление (1.3.2) имеет вид
представление (1.3.2) имеет вид
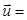 grad
grad 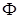 ,
, 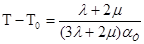 □
□ 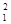
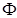 , (1.3.18)
, (1.3.18)
где функция 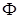 удовлетворяет уравнению
удовлетворяет уравнению
﴾□ 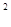 □
□ 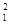
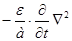 ﴿
﴿ 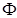 = 0 (1.3.19)
= 0 (1.3.19)
Решение для функции Ф ищют в виде
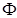 = φ(x, y, z)e
= φ(x, y, z)e 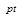 (1.3.20)
(1.3.20)
где р — комплексная постоянная. Подставляя это решение в (1.3.19), для φ получают уравнение
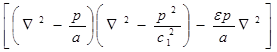 =0. (1.3.21)
=0. (1.3.21)
которое может быть представлено в виде
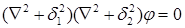 , (1.3.22)(9.3.19)
, (1.3.22)(9.3.19)
Где
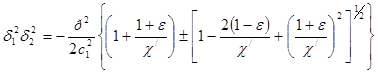 ; (1.3.23)
; (1.3.23)
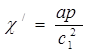
Если предположить, что термоупругая связь отсутствует (ε = 0), то из уравнения (1.3.23) получают
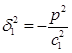 ;
; 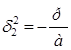 . (1.3.24)
. (1.3.24)
Следовательно, уравнение (1.3.23) описывает распространение двух видов волн расширения, из которых один, связанный с 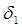 , близок к чисто упругой волне, а другой, связанный с
, близок к чисто упругой волне, а другой, связанный с 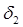 , сходен по своему характеру с чисто тепловой волной.
, сходен по своему характеру с чисто тепловой волной.
На основании уравнений (1.3.20) и (1.3.21) общее решение уравнения (1.3.19) можно представить в виде
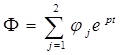 (1.3.25)
(1.3.25)
где 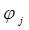 удовлетворяет уравнению
удовлетворяет уравнению
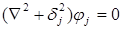 j=1,2. (1.3.26)
j=1,2. (1.3.26)
Таким образом, в рассматриваемом случае общее решение связанной термоупругой задачи на основании представления (1.3.18) и решения (1.3.25) принимает вид
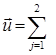 grad
grad 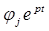 (1.3.27)
(1.3.27)
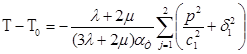
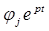 (1.3.28)
(1.3.28)
Учитывая, что
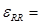 div
div 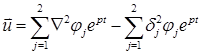
и принимая во внимание формулу (1.328), получаем на основании соотношения (1.2.2) следующие выражения для напряжений:
 (1.3.29)
(1.3.29)
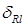 — символ Кронекера;
— символ Кронекера;
ρ — плотность среды, в которой распространяется волна (1.3.26)
Задача термоупругости, описываемая двумя уравнениями:
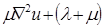 grad div
grad div 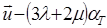 grad (Т — Т0) —
grad (Т — Т0) — 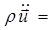 0 , (1.3.30)
0 , (1.3.30)
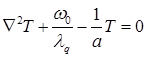 (1.3.31)
(1.3.31)
называется несвязанной динамической задачей термоупругости, или просто динамической задачей термоупругости.
При существенном приращении температуры Т—Т0 коэффициенты 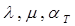 в соотношениях (1.2.2) являются функциями Т, а следовательно, и функциями координат хR и времени t. Помня об этом и выполняя преобразования, аналогичные проведенным в п. 1.3, находим для такой задачи следующие уравнения движения в перемещениях:
в соотношениях (1.2.2) являются функциями Т, а следовательно, и функциями координат хR и времени t. Помня об этом и выполняя преобразования, аналогичные проведенным в п. 1.3, находим для такой задачи следующие уравнения движения в перемещениях:
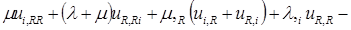
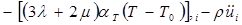 . (1.3.32)
. (1.3.32)
Вместо этих трех скалярных уравнений можно записать одно векторное в виде
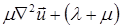 grad div
grad div 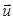 + 2 grad μ·Пε grad λ div
+ 2 grad μ·Пε grad λ div 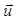 -
-
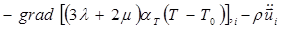 (1.3.33)
(1.3.33)
где grad μ · Пε — скалярное произведение тензора деформации Пε на вектор grad μ.
Если учесть зависимость 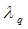 от температуры, то уравнение тепло проводности становится нелинейным.
от температуры, то уравнение тепло проводности становится нелинейным.
Модель термоупругой среды
Дата: 2019-05-29, просмотров: 356.