Содержание
Введение
1 Термодинамические основы термоупругости
1.1 Термоупругость
1.2 Построение задачи термоупругости
1.3 Виды задач: связанная и несвязанная
2 Модель термоупругой среды
2.1 Понятие модели сплошной среды: простые и сложные
2.2 Постановка задач в механике сплошных сред
3 Линейная термоупругая сплошная среда
3.1 Классическая термоупругость
3.2 Термоупругая среда с внутренними параметрами состояния
3.3 Тепловой удар
3.4 Плоские гармонические термоупругие волны расширения в неограниченной среде
3.5 Задача отражения преломления термоупругих волн в матричной формулировке. Коэффициенты отражения преломления
Заключение
Список использованных источников
Введение
В последнее время теория термоупругости получила существенное развитие в связи с важными проблемами, возникающими при разработке новых конструкций паровых и газовых турбин, реактивных и ракетных двигателей, высокоскоростных самолетов, ядерных реакторов и др. Элементы этих конструкций работают в условиях неравномерного нестационарного нагрева, при котором изменяются физико-механические свойства материалов и возникают градиенты температуры, сопровождающиеся неодинаковым тепловым расширением частей элементов.
Неравномерное тепловое расширение в общем случае не может происходить свободно в сплошном теле; оно вызывает тепловые (термические, температурные) напряжения. Знание величины и характера действия тепловых напряжений необходимо для всестороннего анализа прочности конструкции.
Тепловые напряжения сами по себе и в сочетании с механическими напряжениями от внешних сил могут вызвать появление трещин и разрушение конструкции из материала с повышенной хрупкостью. Некоторые материалы при быстром возникновении напряжений, обусловленном действием резко нестационарного температурного поля, становятся хрупкими и не выдерживают теплового удара. Повторное действие тепловых напряжений приводит к термоусталостному разрушению элементов конструкции. Действие тепловых напряжений может вызвать значительную пластическую деформацию, ведущую к полному или прогрессирующему разрушению конструкции, термовыпучивание тонкостенной конструкции и т. п.
Исследования по термоупругости сначала стимулировались задачами о термоупругих напряжениях в элементах конструкций. Они проводились на основе теории, разработанной Дюамелем (1838) и Нейманом (1841), которые исходили из следующего предположения: полная деформация является суммой упругой деформации, связанной с напряжениями обычными соотношениями, и чисто теплового расширения, соответствующего известному из классической теории теплопроводности температурному полю.
С принципиальной точки зрения теория Дюамеля — Неймана [1], [2] для нестационарных тепловых и механических воздействий оказалась ограниченной: она не позволяет строго описать движение упругого тела, связанное с его тепловым состоянием. При определенных условиях нестационарный нагрев сопровождается динамическими эффектами в конструкции.
В общем случае изменение температуры тела происходит не только вследствие подвода тепла от внешних источников, но и в результате самого процесса деформирования. При деформировании тела от механических или тепловых воздействий, протекающих с большой скоростью, возникает так называемый эффект связанности, обусловленный взаимодействием полей деформации и температуры. Он проявляется в образовании и движении тепловых потоков внутри тела, возникновении связанных упругих и тепловых волн, термоупругом рассеянии энергии и т. п.
Последовательное рассмотрение процессов упругого деформирования и теплопроводности в их взаимосвязи возможно только на основе термодинамических соображений. Томсон (1855) [3] впервые применил основные законы термодинамики для изучения свойств упругого тела. Ряд исследователей Л.Д. Ландау и Е.М. Лифшиц (1953) [4] и др. с помощью методов классической термодинамики получили связанные уравнения термоупругости. Однако в рамках классической термодинамики строгий анализ справедлив лишь для изотермического и адиабатического обратимых процессов деформирования. Реальный процесс деформирования, неразрывно связанный с необратимым процессом теплопроводности, является в общем случае также необратимым. Термодинамика необратимых процессов, разработанная в последние годы, позволила более строго поставить задачу о необратимом процессе деформирования и дать единую трактовку механических и тепловых процессов, нашедшую отражение в работах Био (1956), Чедвика (1960), Боли и Уэйнера (I960) и др. В связи с этим более четко определилась теория термоупругости, обобщающая классическую теорию упругости и теорию теплопроводности. Она охватывает следующие явления: перенос тепла теплопроводностью в теле при стационарном и нестационарном теплообмене между ним и внешней средой; термоупругие напряжения, вызванные градиентами температуры; динамические эффекты при резко нестационарных процессах нагрева и, в частности, термоупругие колебания тонкостенных конструкций при тепловом ударе; термомеханические эффекты, обусловленные взаимодействием полей деформации и температуры.
Сановное положение термодинамики необратимых процессов, вытекающее из предположения о локальном термодинамическом равновесии, заключается в том, что первый и второй законы классической термодинамики справедливы и для локально равновесных макроскопических частей системы. Для математического выражения второго закона термодинамики в случае твердых деформируемых тел, состояние которых определяется большим числом независимых переменных, удобной является формулировка, разработанная Н.Н. Шиллером (1897—1901) [5], Каратеодори (1909) [6] и Т.А. Афанасьевой-Эренфест (1925—1928) [7]. В этой формулировке устанавливается общий эмпирический принцип о невозможности определенных процессов — принцип адиабатической недостижимости. Принципы локального термодинамического равновесия и адиабатической недостижимости позволили использовать разработанный Гиббсом (1875—1878) метод термодинамических функций для вывода соотношений между напряжениями и деформациями, выражений для свободной энергии, внутренней энергии, энтропии и связанного уравнения теплопроводности.
В теории термоупругости обычно накладывается ограничение на величину термического возмущения: приращение температуры предполагается малым по сравнению с начальной абсолютной температурой. Снятие этого ограничения не нарушает предположения о малости деформаций, но приводит к появлению нелинейных членов в связанных уравнениях термоупругости. Возможно построение единой теории термоупругости без указанного ограничения в рамках предположения о малости деформаций, учитывающей зависимость упругих и термических коэффициентов от температуры. В общем случае она является нелинейной теорией связанной термоупругости и в качестве частных случаев охватывает как линейную теорию связанной термоупругости при малом термическом возмущении, так и теорию несвязанной термоупругости при большом термическом возмущении, использующую линейные уравнения движения и нелинейное уравнение теплопроводности.
При исследовании динамических задач термоупругости учет связанности полей деформации и температуры дает возможность выявить новые качественные особенности протекания процесса деформирования. Анализ сравнительно простого решения одномерной задачи о распространении плоских гармонических термоупругих волн в неограниченном теле позволяет правильно понять основные черты термоупругих явлений при разных частотах волн и параметрах связанности материала. В качестве основных граничных связанных задач термоупругости следует отметить двумерные задачи о распространении плоских термоупругих волн вдоль поверхности полупространства и продольных термоупругих волн в длинном цилиндре.
Построение решений связанных задач термоупругости для тел конечных размеров вызывает значительные математические трудности. Большой интерес поэтому представляют вариационные принципы связанной термоупругости, и в частности вариационный принцип Био, позволяющие развить приближенные методы решения связанных задач динамической теории упругости и нестационарной теплопроводности.
Все выше сказанное доказывает актуальность и ценность темы термоупругости и изучения ее моделей.
Математические модели и методы термомеханики. В математических моделях термомеханики рассматривают различные способы распространения тепла в сплошных средах. Считается, что распространение тепла может проходить за счет теплопроводности (тепло передается через само вещество), конвекции (тепло передается за счет относительного движения частиц нагретого тела) и излучения (перенос тепла осуществляется за счет электромагнитного излучения). Математические модели теплопроводности были впервые разработаны в XIX в. в работах С. Duhamel и G. Lame [8]. Систематическое изложение методов теплопроводности дано в работах А. В. Лыкова [9], Г. Карслоу, Д. Егеря [10]. Тепло за счет теплопроводности распространяется при наличии распределенных и точечных источников и стоков тепла в теле. Распространение тепла всегда сопровождается также возникновением в теле напряжений, деформаций и, быть может, электромагнитных полей. Исследованию напряженно-деформированного состояния тел с учетом различных связей между напряжениями, деформациями и температурой, а также электромагнитными полями, и составляет основу современных моделей термомеханики. Например, предложены математические модели, в которых отражены зависимость температуры от времени, от теплофизических постоянных материала, различных форм взаимодействия полей температур и деформаций, связи тепловых, упругих и электромагнитных полей, способа задания температурных полей и др. Разработаны математические модели решения задач. Коротко остановимся на некоторых из этих моделей и методов.
Модели термомеханики без учета электромагнитных полей. Основные законы термодинамики для изучения свойств термоупругого тела впервые применил Томсон, а затем развили Н.Н. Шиллер [5], Каратеодори, Т.А. [6] Афанасьева-Эренфест [7]и другие. В этом случае модель получалась динамической и связанной, т.к. в уравнении теплопроводности и уравнениях движения учитывались слагаемые деформационного нагрева и инерционные члены.
Среди работ, посвященных решению связанных задач термоупругости, отметим работы В. Новацкого [11], В.Г. Карнаухова [12], О.П. Червинко, И.К. Сенченкова, Е.В. Доли [13], Л.А. Фильштинского, Ю.В. Сиренко [14] и др.
Термоупругое состояние является следствием уже распределенных температурных полей. Представление общего решения такой задачи в практически удобной форме было предложено в работах П.Ф. Папковича [15], [16]. При этом решение однородного уравнения для вектора перемещения содержит вектор и скаляр, являющиеся произвольными, а частное решение соответствующего неоднородного уравнения, отвечающее уже определенному температурному полю, определяется через скалярную функцию, получившую название термоупругого потенциала перемещений. Первое систематическое изложение теории несвязанной термоупругости для изотропного тела было дано Н.Н. Лебедевым [17], для анизотропного тела И.А. Прусовым [18], А.И. Уздалевым [19].
В линейной теории термоупругости считается, что максимальное изменение температуры мало по отношению к начальной абсолютной температуре. Случай больших изменений температуры в рамках предположения о малости деформации приводит к необходимости учета нелинейных членов в связанных уравнениях термоупругости, а также зависимости тепловых и упругих свойств от температуры.
В рамках предположения о малости деформаций построены модели теории теплопроводности и термоупругости, учитывающие зависимость тепловых и упругих свойств материала от температуры.
Особенно широкое развитие получили теории теплопроводности и термоупругости в случае изотропных пластинок и оболочек, ослабленных отверстиями и трещинами. Для решения таких задач использовались методы комплексных потенциалов, сингулярных интегральных уравнений, функций Грина, малого параметра, дисторсии, интегральных преобразований, асимптотические методы, метод конечных элементов. Наиболее удобными в использовании оказались методы комплексных потенциалов.
Широкие исследования термоупругого состояния были выполнены для анизотропных пластинок, тонких плит и оболочек. Основываясь на исследованиях, [20] А.И. Уздалев для решения плоских задач теплопроводности и термоупругости ввел обобщенные комплексные потенциалы термоупругости, позволившие решить различные задачи для односвязных областей. С использованием метода линейного сопряжения решены некоторые задачи термоупругости для некоторых классов анизотропных материалов. Общий подход к построению комплексных потенциалов и решения задач термоупругости в случае многосвязных пластинок и плит был предложен С.А. Калоеровым и А.С. Космодамианским [21], ими был решен ряд задач, когда на контурах отверстий задавались значения температуры, во внутренних точках действуют сосредоточенные источники тепла.
С использованием методов интегральных преобразований в некоторых работах Р.М. Кушнира, Т.М. Николишина [22], В.А Осадчука, В.П. Шевченко, А.С. Гольцева [23], были решены задачи термоупругости для ортотропных оболочек и пластин.
Достаточно много исследований термоупругого состояния проведено и для термовязкоупругих сред. В э той области можно отметить работы А.А. Ильюшина, Б.Е. Победри [25], В.Г. Карнаухова, И.К. Сенченкова, Б.П. Гуменюка [26], В.Г. Карнаухова И.Ф. Киричок [27], Ю.Н. Шевченко, Ю.Г. Савченко [28]. Разработке теории и методов расчета задач термопластичности посвящены работы Ю.Н. Шевченко [29 – 31].
Особое внимание в задачах термомеханики уделяется способу задания тепловой нагрузки и ее моделированию при решении конкретных задач. В этой области проведен ряд исследований, в которых учитывались различные формы моделирования тепловой нагрузки: задание значений температуры и плотности потоков тепла на границе, сосредоточенных источников тепла, однородных потоков тепла на бесконечности. Сосредоточенный источник тепла, как правило, рассматривается как предельный случай задания на контуре кругового отверстия потока тепла постоянной плотности, когда контур стягивается в точку. Обзору основных моделей и методов термоупругости посвящены статьи В.Г. Карнаухова [32], А.Д. Коваленко [33], [34], В.В. Мелешко [35], T.R. Tauchert [36].
Модели термомеханики с учетом электромагнитных полей. Изучением термомеханического поведения деформируемых твердых тел с учетом электромагнитных полей, связанных с механическими и тепловыми процессами в теле, занимается механика связанных полей. Основные положения моделей механики сплошной среды, учитывающие взаимодействия полей различной физической природы, изложены в работах С.А. Амбарцумяна [37], А.Н. Гузя, Ф. Г. Махорта [38], А.А. Ильюшина [39], Л.Д. Ландау, Е.М. Лившица [4], Ж. Можена, В. Новацкого [40], В.З. Партона, Б.А. Кудрявцева[41], H.A. Haus [42] и др. При построении таких моделей механики деформируемого твердого тела влияние электромагнитного поля на термомеханическое поведение тела реализуется через пондеромоторные силы и их моменты, а также через источники дополнительной энергии, возникающие при взаимодействии тела с внешним электромагнитным полем. При этом формулируются макроскопические уравнения электродинамики Максвелла, описывающие поле во внешней среде и в теле с учетом характеристик поля, таких как токи проводимости, поляризация и намагничивание. На сегодняшний день существуют несколько подходов к получению макроскопических уравнений электродинамики тел, способных к поляризации и намагничиванию, и определению характеристик электромагнитного поля в теле и энергии в нем.
Наиболее распространенными в литературе такими подходами являются статистическая модель, модель Лоренца [43], двудипольная модель и модель Максвелла – Минковского.
В статистической модели [45] путем статистического осреднения в электромагнитных полей и уравнений электродинамики на микроуровне, вызванные движением точечных носителей зарядов (электроны, ядра) в рамках стабильных структур (атомы, молекулы, ионы), определяются макроскопические поля и уравнения Максвелла, причем соотношения для поляризации и намагнивания на макроуровне получаются как средние статистические от магнитного и дипольного моментов в теле.
В модели Лоренца [43], [44] тело считается состоящим из положительно и отрицательно электрически заряженных элементарных частиц, движущихся в вакууме под действием их собственных или внешних полей. В этом случае происходит перераспределение микрозарядов и микротоков в сплошной среде, возникают микроскопические электромагнитные поля. Макроскопические уравнения и поля получаются путем пространственно-временного осреднения уравнений и полей на микроуровне, намагниченность и поляризация понимаются как средние плотности магнитного и дипольного моментов в теле.
При рассмотрении тела в двудипольной модели считается: оно состоит из движущихся материальных частиц-носителей электрических, магнитных зарядов, свободных зарядов и токов, создающие электромагнитное поле в среде. При этом поляризация и намагниченность моделируются электрическими и магнитными диполями, состоящие из пары положительных и отрицательных электрических и магнитных зарядов соответственно. На основе такого представления формулируется макроскопическая система уравнений электродинамики. В этой модели характеристики поля выводятся из предположения, что на каждый заряд в поле действует сила Лоренца, на диполь – момент таких сил.
В модели Максвелла – Минковского в отличии от рассмотренных выше моделей, в которых макроскопические электромагнитные поля и уравнения электродинамики получается путем осреднения полей и уравнений на микро-уровне, уравнения электродинамики для движущегося тела получаются из уравнений Максвелла для неподвижного тела, исходя из предположения Лоренц – инвариантности уравнений электродинамики. Выражения для характеристик поля и энергии получаются из закона сохранения для системы взаимодействия электромагнитного поля и среды, предполагая замкнутость механической и незамкнутость электрических подсистем.
Отметим также, что в литературе предложены и более сложные подходы, учитывающие не только заряды, а и спины, магнитные моменты. При этом, кроме известных электромагнитных сил, вводятся еще и обменные, спин-орбитальные, спин-спиновые силы.
На основе описанных моделей с использованием локально-равновесной или рациональной термодинамики предложены некоторые обобщенные термодинамические модели, описывающие упругую, вязкоупругую, пластическую деформацию тел, способных к поляризации и намагничиванию и обобщающие классические модели линейной термоупругости, а также термовязкоупругости, термовязкопластичности. Кроме уравнения Максвелла, эти модели учитывают различные теплофизические свойства материалов тел, а именно: электропроводимость, пьезоэффект, пироэффект и др.
Исследования термоупругого состояния. Двумерные и плоские задачи. В настоящее время наиболее полно разработаны плоские задачи теплопроводности и термоупругости изотропных и анизотропных сред. Разработке подходов к их решению посвящены монографии Г.С. Кита, М.Г. Кривцуна [46], А.Д. Коваленко [47] , А.С. Космодамианского, С.А. Калоерова [21], Н.Н. Лебедева [17], И.А. Прусова [18], Г.Н. Савина [48], А.И. Уздалева [19]и др. С использованием этих методов решен ряд задач для односвязных и многосвязных сред.
Проведены многочисленные исследования термоупругого состояния изотропной пластинки с отверстием или трещиной. При этом в качестве тепловых воздействий выступали сосредоточенные источники тепла или однородный поток тепла на бесконечности. Много исследований проведено и для многосвязных сред. Например, известны исследования для изотропного кругового диска с отверстиями, включениями или трещинами при действии сосредоточенных источников тепла и разности температур. Решено также множество задач термоупругости для бесконечных изотропных тел с двумя и конечным числом отверстий. В работах решены двоякопериодические задачи теплопроводности и термоупругости для пластинки в случае задания на контурах отверстий постоянной одинаковой температуры, на поверхности пластинки постоянного потока тепла.
В работах С.А. Калоерова, Ю.С. Антонова [49] – [51] предложена методика решения задач теплопроводности и термоупругости для конечных и бесконечных многосвязных анизотропных пластинок c отверстиями и трещинами. Решение построено на использовании теории функции комплексного переменного и удовлетворении граничным условиям методом наименьших квадратов.
Термоупругость
Основное уравнение термоупругости. При термическом расширении изотропное тело деформируется таким образом, что компоненты деформации 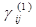 отнесенные к системе прямоугольных осей х1 x2 x3 определяются выражением (1.1.1)
отнесенные к системе прямоугольных осей х1 x2 x3 определяются выражением (1.1.1)
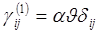 , (1.1.1)
, (1.1.1)
Допускается, что 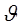 достаточно мало для того, чтобы термические свойства тела оставались постоянными на том отрезке времени, который нас интересует. Суммарная деформация тела выражается через компоненты вектора перемещения u1 следующим уравнением:
достаточно мало для того, чтобы термические свойства тела оставались постоянными на том отрезке времени, который нас интересует. Суммарная деформация тела выражается через компоненты вектора перемещения u1 следующим уравнением:
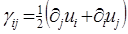 (1.1.2)
(1.1.2)
где 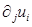 обозначает частную производную
обозначает частную производную 
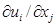 . Эта суммарная деформация состоит из термической деформации и упругой деформации, компоненты которой
. Эта суммарная деформация состоит из термической деформации и упругой деформации, компоненты которой 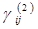 определяются соотношением (1.1.1)
определяются соотношением (1.1.1)
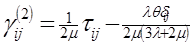 , (1.1.3)
, (1.1.3)
где τij — компоненты тензора напряжений; величина
θ = τij (1.1.4)
является суммой главных напряжений; λ и μ — упругие постоянные Ламе для тела. Подставляя соотношения (1.1.1) — (1.1.3) — в уравнение
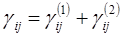
получим тензорное уравнение
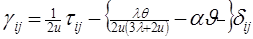 , (1.1.5)
, (1.1.5)
Решая это тензорное уравнение относительно компонентов тензора напряжений, найдем
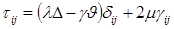 (1.1.6)
(1.1.6)
где
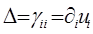 (1.1.7)
(1.1.7)
обозначает расширение тела и
γ = α(3λ + 2μ). (1.1.8)
Физический закон, выраженный тензорным соотношением (1.1.6), называется законом Дюамеля — Неймана
Термодинамическими переменными, описывающими состояние упругого тела, являются компоненты деформации (1.1.2) и абсолютная температура Т + 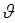 .
.
Используя методы термодинамики обратимых процессов, Био показал, что энтропия s единицы объема тела определяется соотношением
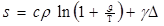 (1.1.9)
(1.1.9)
где аддитивная постоянная, входящая в определение энтропии, была выбрана таким образом, что энтропия была равна нулю в начальном состоянии. В этом уравнении ρ — плотность тела, с — удельная теплоемкость единицы массы (принимаемая независимой от температуры вблизи равновесной температуры T), и γ определяется формулой (1.1.8). Если 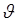 мало по сравнению с Т то соотношение (1.1.9) сводится к простому выражению для энтропии единицы объема
мало по сравнению с Т то соотношение (1.1.9) сводится к простому выражению для энтропии единицы объема
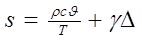 (1.1.10)
(1.1.10)
Таким образом, количество тепла, поглощаемое единицей объема в процессе малых деформаций и малых изменении температуры, определяется формулой
h=Ts = ρс 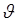 + γTΔ (1.1.11)
+ γTΔ (1.1.11)
Из теории теплопроводности в твердых телах известно, что изменение температуры внутри изотропного тела подчиняется уравнению
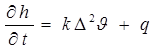 (1.1.12)
(1.1.12)
k — коэффициент теплопроводности тела;
q — количество тепла;
выделяемого в единице объема тела. Подставляя выражение (1.1.10) в соотношение (1.1.11), найдем
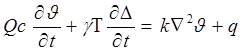 (1.1.13)
(1.1.13)
Если ввести коэффициент температуропроводности
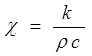 ,
,
то последнее уравнение можно записать в форме
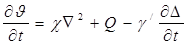 (1.1.14) где
(1.1.14) где
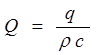 ,
, 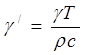
Для того чтобы дополнить систему основных уравнений, присоединим к ней уравнения движения в виде
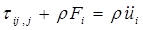 , (1.1.15)
, (1.1.15)
где (F1 , F2 ,F3) обозначает массовую силу в точке (х1, х2 , х3) и — i-й компонент ускорения д2и/дt2 бес конечно малого элемента, сосредоточенного около этой точки.
Система шестнадцати уравнений (1.1.2), (1.1.6), (1.1.14) и (1.1.15) вместе с соответствующими граничными условиями достаточна для определения изменения температуры и компонентой напряжений и перемещения в случае» когда источники тепла и массовые силы заданы.
Безразмерная форма уравнений. Основные уравнения термоупругости удобно записать в безразмерной форме. Если характерный линейный размер 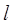 принять в качестве единицы длины» время τ в качестве единицы времени, температуру начала отсчета T за единицу измерения температуры и модуль сдвига μ принять в качестве единицы измерения, напряжения то в результате найдем, что уравнения (1.1.6), (1.1.14) и (1.1.15) примут соответственно следующую безразмерную форму:
принять в качестве единицы длины» время τ в качестве единицы времени, температуру начала отсчета T за единицу измерения температуры и модуль сдвига μ принять в качестве единицы измерения, напряжения то в результате найдем, что уравнения (1.1.6), (1.1.14) и (1.1.15) примут соответственно следующую безразмерную форму:
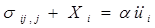 , (1.1.16)
, (1.1.16)
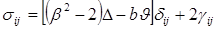 (1.1.17)
(1.1.17)
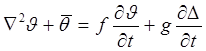 где
где
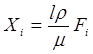 ,
, 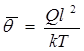
обозначают новые функции и
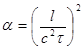 ,
, 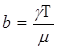 ,
, 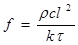 ,
, 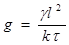 .
.
При определении а величина 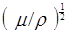 была заменена скоростью с2 распространения S-волн в теле. Величинa
была заменена скоростью с2 распространения S-волн в теле. Величинa 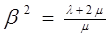 представляет квадрат отношения скорости Р – волн к скорости S – воли. В зависимости от коэффициента Пуассона величину β можно записать в виде
представляет квадрат отношения скорости Р – волн к скорости S – воли. В зависимости от коэффициента Пуассона величину β можно записать в виде 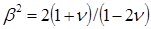 .
.
Задачи об установившихся состояниях. Если массовые силы и источники тепла не зависят от времени и если поверхностные нагрузки являются статическими нагрузками, то тогда основная система уравнений (1.1.16), (1.1.14) и (1.1.15) примет вид
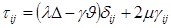 (1.1.19)
(1.1.19)
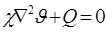 , (1.1.20)
, (1.1.20)
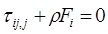 (1.1.21)
(1.1.21)
Подставив в уравнение (1.1.19) модуль Юнга Е и коэффициент Пуассона υ, получим следующее уравнение:
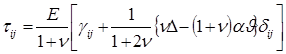 (1.1.22)
(1.1.22)
Для упругого тела, свободного от массовых сил, полагая Fi = 0 и используя формулу
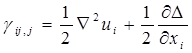
найдем, подставляя соотношение (1.1.22) в уравнение (1.1.21):
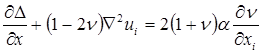 (1.1.23)
(1.1.23)
Для того чтобы решить это уравнение, Гудьер вводит термоупругий потенциал φ, с помощью которого вектор перемещения u1, u2, и3 определяется в виде
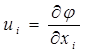 (1.1.24)
(1.1.24)
Подставляя выражение (1.1.24) в уравнение (1.1.23), получаем условие, накладываемое на φ:
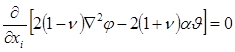
Таким образом, если выбрать φ так, что
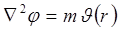 , (1.1.25)
, (1.1.25)
где
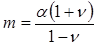
то вектор перемещения, определяемый уравнением (1.1.24), является решением уравнений, описывающих установившийся процесс термоупругости.Уравнение (1.1.25) в точности соответствует уравнению Пуассона и хорошо известно, что частный интеграл этого уравнения имеет вид
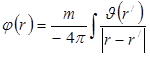 (1.1.26)
(1.1.26)
где интегрирование распространяется на все тело.
Напряженное и деформированное состояния, представляемые частным интегралом (1.1.26), требуют не только заданного распределения температуры, но также и определенных поверхностных нагрузок, которые могут быть вычислены посредством выражения (1.1.22) и условии равновесия на границе. Для полного решения задачи требуется лишь определить распределение дополнительных напряжениий, обусловленных равными и прямо противоположными нагрузками на границе, что представляет собой задачу теории упругости при заданных нагрузках на границе. Тот факт, что тело нагрето, не играет роли до тех пор, пока упругие постоянные остаются неизменными. Интегралы типа (1.1.26) были использованы Борхардтом при общем анализе теории термоупругости и при решении некоторых частных задач в случае несимметричных распределений температуры в теле со сферическими или цилиндрическими границами. Распределение напряжений, обусловленное специальным распределением температуры в бесконечном и полубесконечном телах, обсуждалось различными авторами. Имеется очень мало точных решений даже этих уравнений, описывающих установившееся состояние, а те, которые имеются, относятся к сферам и цилиндрам, однако в главе 14 книги Тимошенко и Гудиера «Theory of Elasticity» (New York, 1951) рассматривается несколько приближенных решений инженерных задач, касающихся термических напряжений в пластинах и стержнях
Модель термоупругой среды
Содержание
Введение
1 Термодинамические основы термоупругости
1.1 Термоупругость
1.2 Построение задачи термоупругости
1.3 Виды задач: связанная и несвязанная
2 Модель термоупругой среды
2.1 Понятие модели сплошной среды: простые и сложные
2.2 Постановка задач в механике сплошных сред
3 Линейная термоупругая сплошная среда
3.1 Классическая термоупругость
3.2 Термоупругая среда с внутренними параметрами состояния
3.3 Тепловой удар
3.4 Плоские гармонические термоупругие волны расширения в неограниченной среде
3.5 Задача отражения преломления термоупругих волн в матричной формулировке. Коэффициенты отражения преломления
Заключение
Список использованных источников
Введение
В последнее время теория термоупругости получила существенное развитие в связи с важными проблемами, возникающими при разработке новых конструкций паровых и газовых турбин, реактивных и ракетных двигателей, высокоскоростных самолетов, ядерных реакторов и др. Элементы этих конструкций работают в условиях неравномерного нестационарного нагрева, при котором изменяются физико-механические свойства материалов и возникают градиенты температуры, сопровождающиеся неодинаковым тепловым расширением частей элементов.
Неравномерное тепловое расширение в общем случае не может происходить свободно в сплошном теле; оно вызывает тепловые (термические, температурные) напряжения. Знание величины и характера действия тепловых напряжений необходимо для всестороннего анализа прочности конструкции.
Тепловые напряжения сами по себе и в сочетании с механическими напряжениями от внешних сил могут вызвать появление трещин и разрушение конструкции из материала с повышенной хрупкостью. Некоторые материалы при быстром возникновении напряжений, обусловленном действием резко нестационарного температурного поля, становятся хрупкими и не выдерживают теплового удара. Повторное действие тепловых напряжений приводит к термоусталостному разрушению элементов конструкции. Действие тепловых напряжений может вызвать значительную пластическую деформацию, ведущую к полному или прогрессирующему разрушению конструкции, термовыпучивание тонкостенной конструкции и т. п.
Исследования по термоупругости сначала стимулировались задачами о термоупругих напряжениях в элементах конструкций. Они проводились на основе теории, разработанной Дюамелем (1838) и Нейманом (1841), которые исходили из следующего предположения: полная деформация является суммой упругой деформации, связанной с напряжениями обычными соотношениями, и чисто теплового расширения, соответствующего известному из классической теории теплопроводности температурному полю.
С принципиальной точки зрения теория Дюамеля — Неймана [1], [2] для нестационарных тепловых и механических воздействий оказалась ограниченной: она не позволяет строго описать движение упругого тела, связанное с его тепловым состоянием. При определенных условиях нестационарный нагрев сопровождается динамическими эффектами в конструкции.
В общем случае изменение температуры тела происходит не только вследствие подвода тепла от внешних источников, но и в результате самого процесса деформирования. При деформировании тела от механических или тепловых воздействий, протекающих с большой скоростью, возникает так называемый эффект связанности, обусловленный взаимодействием полей деформации и температуры. Он проявляется в образовании и движении тепловых потоков внутри тела, возникновении связанных упругих и тепловых волн, термоупругом рассеянии энергии и т. п.
Последовательное рассмотрение процессов упругого деформирования и теплопроводности в их взаимосвязи возможно только на основе термодинамических соображений. Томсон (1855) [3] впервые применил основные законы термодинамики для изучения свойств упругого тела. Ряд исследователей Л.Д. Ландау и Е.М. Лифшиц (1953) [4] и др. с помощью методов классической термодинамики получили связанные уравнения термоупругости. Однако в рамках классической термодинамики строгий анализ справедлив лишь для изотермического и адиабатического обратимых процессов деформирования. Реальный процесс деформирования, неразрывно связанный с необратимым процессом теплопроводности, является в общем случае также необратимым. Термодинамика необратимых процессов, разработанная в последние годы, позволила более строго поставить задачу о необратимом процессе деформирования и дать единую трактовку механических и тепловых процессов, нашедшую отражение в работах Био (1956), Чедвика (1960), Боли и Уэйнера (I960) и др. В связи с этим более четко определилась теория термоупругости, обобщающая классическую теорию упругости и теорию теплопроводности. Она охватывает следующие явления: перенос тепла теплопроводностью в теле при стационарном и нестационарном теплообмене между ним и внешней средой; термоупругие напряжения, вызванные градиентами температуры; динамические эффекты при резко нестационарных процессах нагрева и, в частности, термоупругие колебания тонкостенных конструкций при тепловом ударе; термомеханические эффекты, обусловленные взаимодействием полей деформации и температуры.
Сановное положение термодинамики необратимых процессов, вытекающее из предположения о локальном термодинамическом равновесии, заключается в том, что первый и второй законы классической термодинамики справедливы и для локально равновесных макроскопических частей системы. Для математического выражения второго закона термодинамики в случае твердых деформируемых тел, состояние которых определяется большим числом независимых переменных, удобной является формулировка, разработанная Н.Н. Шиллером (1897—1901) [5], Каратеодори (1909) [6] и Т.А. Афанасьевой-Эренфест (1925—1928) [7]. В этой формулировке устанавливается общий эмпирический принцип о невозможности определенных процессов — принцип адиабатической недостижимости. Принципы локального термодинамического равновесия и адиабатической недостижимости позволили использовать разработанный Гиббсом (1875—1878) метод термодинамических функций для вывода соотношений между напряжениями и деформациями, выражений для свободной энергии, внутренней энергии, энтропии и связанного уравнения теплопроводности.
В теории термоупругости обычно накладывается ограничение на величину термического возмущения: приращение температуры предполагается малым по сравнению с начальной абсолютной температурой. Снятие этого ограничения не нарушает предположения о малости деформаций, но приводит к появлению нелинейных членов в связанных уравнениях термоупругости. Возможно построение единой теории термоупругости без указанного ограничения в рамках предположения о малости деформаций, учитывающей зависимость упругих и термических коэффициентов от температуры. В общем случае она является нелинейной теорией связанной термоупругости и в качестве частных случаев охватывает как линейную теорию связанной термоупругости при малом термическом возмущении, так и теорию несвязанной термоупругости при большом термическом возмущении, использующую линейные уравнения движения и нелинейное уравнение теплопроводности.
При исследовании динамических задач термоупругости учет связанности полей деформации и температуры дает возможность выявить новые качественные особенности протекания процесса деформирования. Анализ сравнительно простого решения одномерной задачи о распространении плоских гармонических термоупругих волн в неограниченном теле позволяет правильно понять основные черты термоупругих явлений при разных частотах волн и параметрах связанности материала. В качестве основных граничных связанных задач термоупругости следует отметить двумерные задачи о распространении плоских термоупругих волн вдоль поверхности полупространства и продольных термоупругих волн в длинном цилиндре.
Построение решений связанных задач термоупругости для тел конечных размеров вызывает значительные математические трудности. Большой интерес поэтому представляют вариационные принципы связанной термоупругости, и в частности вариационный принцип Био, позволяющие развить приближенные методы решения связанных задач динамической теории упругости и нестационарной теплопроводности.
Все выше сказанное доказывает актуальность и ценность темы термоупругости и изучения ее моделей.
Математические модели и методы термомеханики. В математических моделях термомеханики рассматривают различные способы распространения тепла в сплошных средах. Считается, что распространение тепла может проходить за счет теплопроводности (тепло передается через само вещество), конвекции (тепло передается за счет относительного движения частиц нагретого тела) и излучения (перенос тепла осуществляется за счет электромагнитного излучения). Математические модели теплопроводности были впервые разработаны в XIX в. в работах С. Duhamel и G. Lame [8]. Систематическое изложение методов теплопроводности дано в работах А. В. Лыкова [9], Г. Карслоу, Д. Егеря [10]. Тепло за счет теплопроводности распространяется при наличии распределенных и точечных источников и стоков тепла в теле. Распространение тепла всегда сопровождается также возникновением в теле напряжений, деформаций и, быть может, электромагнитных полей. Исследованию напряженно-деформированного состояния тел с учетом различных связей между напряжениями, деформациями и температурой, а также электромагнитными полями, и составляет основу современных моделей термомеханики. Например, предложены математические модели, в которых отражены зависимость температуры от времени, от теплофизических постоянных материала, различных форм взаимодействия полей температур и деформаций, связи тепловых, упругих и электромагнитных полей, способа задания температурных полей и др. Разработаны математические модели решения задач. Коротко остановимся на некоторых из этих моделей и методов.
Модели термомеханики без учета электромагнитных полей. Основные законы термодинамики для изучения свойств термоупругого тела впервые применил Томсон, а затем развили Н.Н. Шиллер [5], Каратеодори, Т.А. [6] Афанасьева-Эренфест [7]и другие. В этом случае модель получалась динамической и связанной, т.к. в уравнении теплопроводности и уравнениях движения учитывались слагаемые деформационного нагрева и инерционные члены.
Среди работ, посвященных решению связанных задач термоупругости, отметим работы В. Новацкого [11], В.Г. Карнаухова [12], О.П. Червинко, И.К. Сенченкова, Е.В. Доли [13], Л.А. Фильштинского, Ю.В. Сиренко [14] и др.
Термоупругое состояние является следствием уже распределенных температурных полей. Представление общего решения такой задачи в практически удобной форме было предложено в работах П.Ф. Папковича [15], [16]. При этом решение однородного уравнения для вектора перемещения содержит вектор и скаляр, являющиеся произвольными, а частное решение соответствующего неоднородного уравнения, отвечающее уже определенному температурному полю, определяется через скалярную функцию, получившую название термоупругого потенциала перемещений. Первое систематическое изложение теории несвязанной термоупругости для изотропного тела было дано Н.Н. Лебедевым [17], для анизотропного тела И.А. Прусовым [18], А.И. Уздалевым [19].
В линейной теории термоупругости считается, что максимальное изменение температуры мало по отношению к начальной абсолютной температуре. Случай больших изменений температуры в рамках предположения о малости деформации приводит к необходимости учета нелинейных членов в связанных уравнениях термоупругости, а также зависимости тепловых и упругих свойств от температуры.
В рамках предположения о малости деформаций построены модели теории теплопроводности и термоупругости, учитывающие зависимость тепловых и упругих свойств материала от температуры.
Особенно широкое развитие получили теории теплопроводности и термоупругости в случае изотропных пластинок и оболочек, ослабленных отверстиями и трещинами. Для решения таких задач использовались методы комплексных потенциалов, сингулярных интегральных уравнений, функций Грина, малого параметра, дисторсии, интегральных преобразований, асимптотические методы, метод конечных элементов. Наиболее удобными в использовании оказались методы комплексных потенциалов.
Широкие исследования термоупругого состояния были выполнены для анизотропных пластинок, тонких плит и оболочек. Основываясь на исследованиях, [20] А.И. Уздалев для решения плоских задач теплопроводности и термоупругости ввел обобщенные комплексные потенциалы термоупругости, позволившие решить различные задачи для односвязных областей. С использованием метода линейного сопряжения решены некоторые задачи термоупругости для некоторых классов анизотропных материалов. Общий подход к построению комплексных потенциалов и решения задач термоупругости в случае многосвязных пластинок и плит был предложен С.А. Калоеровым и А.С. Космодамианским [21], ими был решен ряд задач, когда на контурах отверстий задавались значения температуры, во внутренних точках действуют сосредоточенные источники тепла.
С использованием методов интегральных преобразований в некоторых работах Р.М. Кушнира, Т.М. Николишина [22], В.А Осадчука, В.П. Шевченко, А.С. Гольцева [23], были решены задачи термоупругости для ортотропных оболочек и пластин.
Достаточно много исследований термоупругого состояния проведено и для термовязкоупругих сред. В э той области можно отметить работы А.А. Ильюшина, Б.Е. Победри [25], В.Г. Карнаухова, И.К. Сенченкова, Б.П. Гуменюка [26], В.Г. Карнаухова И.Ф. Киричок [27], Ю.Н. Шевченко, Ю.Г. Савченко [28]. Разработке теории и методов расчета задач термопластичности посвящены работы Ю.Н. Шевченко [29 – 31].
Особое внимание в задачах термомеханики уделяется способу задания тепловой нагрузки и ее моделированию при решении конкретных задач. В этой области проведен ряд исследований, в которых учитывались различные формы моделирования тепловой нагрузки: задание значений температуры и плотности потоков тепла на границе, сосредоточенных источников тепла, однородных потоков тепла на бесконечности. Сосредоточенный источник тепла, как правило, рассматривается как предельный случай задания на контуре кругового отверстия потока тепла постоянной плотности, когда контур стягивается в точку. Обзору основных моделей и методов термоупругости посвящены статьи В.Г. Карнаухова [32], А.Д. Коваленко [33], [34], В.В. Мелешко [35], T.R. Tauchert [36].
Модели термомеханики с учетом электромагнитных полей. Изучением термомеханического поведения деформируемых твердых тел с учетом электромагнитных полей, связанных с механическими и тепловыми процессами в теле, занимается механика связанных полей. Основные положения моделей механики сплошной среды, учитывающие взаимодействия полей различной физической природы, изложены в работах С.А. Амбарцумяна [37], А.Н. Гузя, Ф. Г. Махорта [38], А.А. Ильюшина [39], Л.Д. Ландау, Е.М. Лившица [4], Ж. Можена, В. Новацкого [40], В.З. Партона, Б.А. Кудрявцева[41], H.A. Haus [42] и др. При построении таких моделей механики деформируемого твердого тела влияние электромагнитного поля на термомеханическое поведение тела реализуется через пондеромоторные силы и их моменты, а также через источники дополнительной энергии, возникающие при взаимодействии тела с внешним электромагнитным полем. При этом формулируются макроскопические уравнения электродинамики Максвелла, описывающие поле во внешней среде и в теле с учетом характеристик поля, таких как токи проводимости, поляризация и намагничивание. На сегодняшний день существуют несколько подходов к получению макроскопических уравнений электродинамики тел, способных к поляризации и намагничиванию, и определению характеристик электромагнитного поля в теле и энергии в нем.
Наиболее распространенными в литературе такими подходами являются статистическая модель, модель Лоренца [43], двудипольная модель и модель Максвелла – Минковского.
В статистической модели [45] путем статистического осреднения в электромагнитных полей и уравнений электродинамики на микроуровне, вызванные движением точечных носителей зарядов (электроны, ядра) в рамках стабильных структур (атомы, молекулы, ионы), определяются макроскопические поля и уравнения Максвелла, причем соотношения для поляризации и намагнивания на макроуровне получаются как средние статистические от магнитного и дипольного моментов в теле.
В модели Лоренца [43], [44] тело считается состоящим из положительно и отрицательно электрически заряженных элементарных частиц, движущихся в вакууме под действием их собственных или внешних полей. В этом случае происходит перераспределение микрозарядов и микротоков в сплошной среде, возникают микроскопические электромагнитные поля. Макроскопические уравнения и поля получаются путем пространственно-временного осреднения уравнений и полей на микроуровне, намагниченность и поляризация понимаются как средние плотности магнитного и дипольного моментов в теле.
При рассмотрении тела в двудипольной модели считается: оно состоит из движущихся материальных частиц-носителей электрических, магнитных зарядов, свободных зарядов и токов, создающие электромагнитное поле в среде. При этом поляризация и намагниченность моделируются электрическими и магнитными диполями, состоящие из пары положительных и отрицательных электрических и магнитных зарядов соответственно. На основе такого представления формулируется макроскопическая система уравнений электродинамики. В этой модели характеристики поля выводятся из предположения, что на каждый заряд в поле действует сила Лоренца, на диполь – момент таких сил.
В модели Максвелла – Минковского в отличии от рассмотренных выше моделей, в которых макроскопические электромагнитные поля и уравнения электродинамики получается путем осреднения полей и уравнений на микро-уровне, уравнения электродинамики для движущегося тела получаются из уравнений Максвелла для неподвижного тела, исходя из предположения Лоренц – инвариантности уравнений электродинамики. Выражения для характеристик поля и энергии получаются из закона сохранения для системы взаимодействия электромагнитного поля и среды, предполагая замкнутость механической и незамкнутость электрических подсистем.
Отметим также, что в литературе предложены и более сложные подходы, учитывающие не только заряды, а и спины, магнитные моменты. При этом, кроме известных электромагнитных сил, вводятся еще и обменные, спин-орбитальные, спин-спиновые силы.
На основе описанных моделей с использованием локально-равновесной или рациональной термодинамики предложены некоторые обобщенные термодинамические модели, описывающие упругую, вязкоупругую, пластическую деформацию тел, способных к поляризации и намагничиванию и обобщающие классические модели линейной термоупругости, а также термовязкоупругости, термовязкопластичности. Кроме уравнения Максвелла, эти модели учитывают различные теплофизические свойства материалов тел, а именно: электропроводимость, пьезоэффект, пироэффект и др.
Исследования термоупругого состояния. Двумерные и плоские задачи. В настоящее время наиболее полно разработаны плоские задачи теплопроводности и термоупругости изотропных и анизотропных сред. Разработке подходов к их решению посвящены монографии Г.С. Кита, М.Г. Кривцуна [46], А.Д. Коваленко [47] , А.С. Космодамианского, С.А. Калоерова [21], Н.Н. Лебедева [17], И.А. Прусова [18], Г.Н. Савина [48], А.И. Уздалева [19]и др. С использованием этих методов решен ряд задач для односвязных и многосвязных сред.
Проведены многочисленные исследования термоупругого состояния изотропной пластинки с отверстием или трещиной. При этом в качестве тепловых воздействий выступали сосредоточенные источники тепла или однородный поток тепла на бесконечности. Много исследований проведено и для многосвязных сред. Например, известны исследования для изотропного кругового диска с отверстиями, включениями или трещинами при действии сосредоточенных источников тепла и разности температур. Решено также множество задач термоупругости для бесконечных изотропных тел с двумя и конечным числом отверстий. В работах решены двоякопериодические задачи теплопроводности и термоупругости для пластинки в случае задания на контурах отверстий постоянной одинаковой температуры, на поверхности пластинки постоянного потока тепла.
В работах С.А. Калоерова, Ю.С. Антонова [49] – [51] предложена методика решения задач теплопроводности и термоупругости для конечных и бесконечных многосвязных анизотропных пластинок c отверстиями и трещинами. Решение построено на использовании теории функции комплексного переменного и удовлетворении граничным условиям методом наименьших квадратов.
Термодинамические основы термоупругости
Термоупругость
Основное уравнение термоупругости. При термическом расширении изотропное тело деформируется таким образом, что компоненты деформации 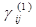 отнесенные к системе прямоугольных осей х1 x2 x3 определяются выражением (1.1.1)
отнесенные к системе прямоугольных осей х1 x2 x3 определяются выражением (1.1.1)
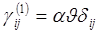 , (1.1.1)
, (1.1.1)
Допускается, что 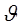 достаточно мало для того, чтобы термические свойства тела оставались постоянными на том отрезке времени, который нас интересует. Суммарная деформация тела выражается через компоненты вектора перемещения u1 следующим уравнением:
достаточно мало для того, чтобы термические свойства тела оставались постоянными на том отрезке времени, который нас интересует. Суммарная деформация тела выражается через компоненты вектора перемещения u1 следующим уравнением:
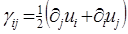 (1.1.2)
(1.1.2)
где 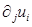 обозначает частную производную
обозначает частную производную 
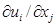 . Эта суммарная деформация состоит из термической деформации и упругой деформации, компоненты которой
. Эта суммарная деформация состоит из термической деформации и упругой деформации, компоненты которой 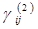 определяются соотношением (1.1.1)
определяются соотношением (1.1.1)
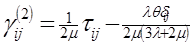 , (1.1.3)
, (1.1.3)
где τij — компоненты тензора напряжений; величина
θ = τij (1.1.4)
является суммой главных напряжений; λ и μ — упругие постоянные Ламе для тела. Подставляя соотношения (1.1.1) — (1.1.3) — в уравнение
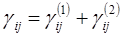
получим тензорное уравнение
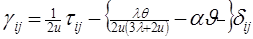 , (1.1.5)
, (1.1.5)
Решая это тензорное уравнение относительно компонентов тензора напряжений, найдем
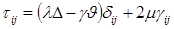 (1.1.6)
(1.1.6)
где
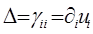 (1.1.7)
(1.1.7)
обозначает расширение тела и
γ = α(3λ + 2μ). (1.1.8)
Физический закон, выраженный тензорным соотношением (1.1.6), называется законом Дюамеля — Неймана
Термодинамическими переменными, описывающими состояние упругого тела, являются компоненты деформации (1.1.2) и абсолютная температура Т + 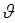 .
.
Используя методы термодинамики обратимых процессов, Био показал, что энтропия s единицы объема тела определяется соотношением
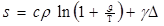 (1.1.9)
(1.1.9)
где аддитивная постоянная, входящая в определение энтропии, была выбрана таким образом, что энтропия была равна нулю в начальном состоянии. В этом уравнении ρ — плотность тела, с — удельная теплоемкость единицы массы (принимаемая независимой от температуры вблизи равновесной температуры T), и γ определяется формулой (1.1.8). Если 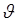 мало по сравнению с Т то соотношение (1.1.9) сводится к простому выражению для энтропии единицы объема
мало по сравнению с Т то соотношение (1.1.9) сводится к простому выражению для энтропии единицы объема
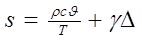 (1.1.10)
(1.1.10)
Таким образом, количество тепла, поглощаемое единицей объема в процессе малых деформаций и малых изменении температуры, определяется формулой
h=Ts = ρс 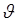 + γTΔ (1.1.11)
+ γTΔ (1.1.11)
Из теории теплопроводности в твердых телах известно, что изменение температуры внутри изотропного тела подчиняется уравнению
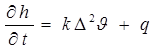 (1.1.12)
(1.1.12)
k — коэффициент теплопроводности тела;
q — количество тепла;
выделяемого в единице объема тела. Подставляя выражение (1.1.10) в соотношение (1.1.11), найдем
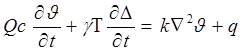 (1.1.13)
(1.1.13)
Если ввести коэффициент температуропроводности
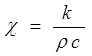 ,
,
то последнее уравнение можно записать в форме
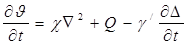 (1.1.14) где
(1.1.14) где
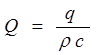 ,
, 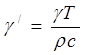
Для того чтобы дополнить систему основных уравнений, присоединим к ней уравнения движения в виде
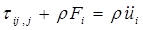 , (1.1.15)
, (1.1.15)
где (F1 , F2 ,F3) обозначает массовую силу в точке (х1, х2 , х3) и — i-й компонент ускорения д2и/дt2 бес конечно малого элемента, сосредоточенного около этой точки.
Система шестнадцати уравнений (1.1.2), (1.1.6), (1.1.14) и (1.1.15) вместе с соответствующими граничными условиями достаточна для определения изменения температуры и компонентой напряжений и перемещения в случае» когда источники тепла и массовые силы заданы.
Безразмерная форма уравнений. Основные уравнения термоупругости удобно записать в безразмерной форме. Если характерный линейный размер 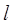 принять в качестве единицы длины» время τ в качестве единицы времени, температуру начала отсчета T за единицу измерения температуры и модуль сдвига μ принять в качестве единицы измерения, напряжения то в результате найдем, что уравнения (1.1.6), (1.1.14) и (1.1.15) примут соответственно следующую безразмерную форму:
принять в качестве единицы длины» время τ в качестве единицы времени, температуру начала отсчета T за единицу измерения температуры и модуль сдвига μ принять в качестве единицы измерения, напряжения то в результате найдем, что уравнения (1.1.6), (1.1.14) и (1.1.15) примут соответственно следующую безразмерную форму:
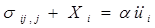 , (1.1.16)
, (1.1.16)
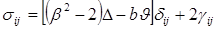 (1.1.17)
(1.1.17)
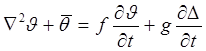 где
где
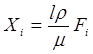 ,
, 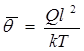
обозначают новые функции и
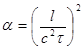 ,
, 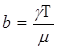 ,
, 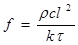 ,
, 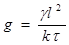 .
.
При определении а величина 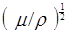 была заменена скоростью с2 распространения S-волн в теле. Величинa
была заменена скоростью с2 распространения S-волн в теле. Величинa 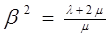 представляет квадрат отношения скорости Р – волн к скорости S – воли. В зависимости от коэффициента Пуассона величину β можно записать в виде
представляет квадрат отношения скорости Р – волн к скорости S – воли. В зависимости от коэффициента Пуассона величину β можно записать в виде 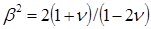 .
.
Задачи об установившихся состояниях. Если массовые силы и источники тепла не зависят от времени и если поверхностные нагрузки являются статическими нагрузками, то тогда основная система уравнений (1.1.16), (1.1.14) и (1.1.15) примет вид
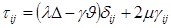 (1.1.19)
(1.1.19)
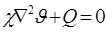 , (1.1.20)
, (1.1.20)
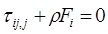 (1.1.21)
(1.1.21)
Подставив в уравнение (1.1.19) модуль Юнга Е и коэффициент Пуассона υ, получим следующее уравнение:
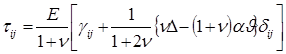 (1.1.22)
(1.1.22)
Для упругого тела, свободного от массовых сил, полагая Fi = 0 и используя формулу
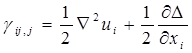
найдем, подставляя соотношение (1.1.22) в уравнение (1.1.21):
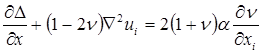 (1.1.23)
(1.1.23)
Для того чтобы решить это уравнение, Гудьер вводит термоупругий потенциал φ, с помощью которого вектор перемещения u1, u2, и3 определяется в виде
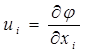 (1.1.24)
(1.1.24)
Подставляя выражение (1.1.24) в уравнение (1.1.23), получаем условие, накладываемое на φ:
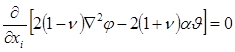
Таким образом, если выбрать φ так, что
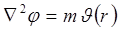 , (1.1.25)
, (1.1.25)
где
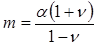
то вектор перемещения, определяемый уравнением (1.1.24), является решением уравнений, описывающих установившийся процесс термоупругости.Уравнение (1.1.25) в точности соответствует уравнению Пуассона и хорошо известно, что частный интеграл этого уравнения имеет вид
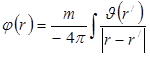 (1.1.26)
(1.1.26)
где интегрирование распространяется на все тело.
Напряженное и деформированное состояния, представляемые частным интегралом (1.1.26), требуют не только заданного распределения температуры, но также и определенных поверхностных нагрузок, которые могут быть вычислены посредством выражения (1.1.22) и условии равновесия на границе. Для полного решения задачи требуется лишь определить распределение дополнительных напряжениий, обусловленных равными и прямо противоположными нагрузками на границе, что представляет собой задачу теории упругости при заданных нагрузках на границе. Тот факт, что тело нагрето, не играет роли до тех пор, пока упругие постоянные остаются неизменными. Интегралы типа (1.1.26) были использованы Борхардтом при общем анализе теории термоупругости и при решении некоторых частных задач в случае несимметричных распределений температуры в теле со сферическими или цилиндрическими границами. Распределение напряжений, обусловленное специальным распределением температуры в бесконечном и полубесконечном телах, обсуждалось различными авторами. Имеется очень мало точных решений даже этих уравнений, описывающих установившееся состояние, а те, которые имеются, относятся к сферам и цилиндрам, однако в главе 14 книги Тимошенко и Гудиера «Theory of Elasticity» (New York, 1951) рассматривается несколько приближенных решений инженерных задач, касающихся термических напряжений в пластинах и стержнях
Дата: 2019-05-29, просмотров: 370.