Экономика содержит в себе объективную необходимость и возможность оптимального развития. Количественный анализ и математическая формулировка экономических законов служит переходной ступенью от их качественной трактовки к разработке моделей оптимального развития. При математической интерпретации экономических законов следует исходить из того, что закон, представляющий причинно-следственную связь производственных отношений, имеет некоторую количественную форму выражения. В качестве материального носителя при этом предполагается рассматривать в основном различные формы общественного продукта. В исследуемой оптимизационной модели в качестве критерия оптимальности предполагается максимизировать дисконтированную сумму конечного (непроизводственного) потребления в течение срока прогнозирования (планирования) [0;T]:

                              J= 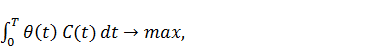(2.11)

где C(t) – непроизводственное потребление; θ(t) – функция дисконтирования, отражающая меру предпочтения потребления в данный момент t относительно потребления того же продукта в последующие моменты. Принято считать, что max θ (t)=θ (0)  и 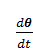 > 0.

Итак, если стоит задача оптимального развития экономики, то ее можно сформулировать следующим образом: определить такой вариант выпуска продукции X(t) и такое непроизводственное потребление C(t), которые обеспечат наибольшее интегральное дисконтированное потребление.                                             

Для экономики, распределение продукции которой определено дифференциальным уравнением связи (см. дискретный аналог (2.6)).

                               X(t) = a X(t) + q 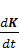+ μ K + C(t),

выпуск продукции ограничен производственной функцией F(t,R,L)                                                                   

                                          0≤ X≤ F(t, R, L),                                                                                            

а рост производственных фондов ограничен снизу:

                                  K(t) ≥ Kзадан  и X( ) = .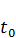

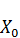Необходимо найти такой вариант развития, который обеспечивает максимум функционала (2.11). Итак, рассмотренная однопродуктовая модель учитывает не только динамику развития экономики, но и цель этого развития. Количественное определение оптимального варианта развития экономики с помощью этой модели связано с использованием аппарата ТОУ.

Глава 3. Моделирование экономической динамики в форме задачи оптимального управления

Примеры задач оптимального управления экономическими системами

Пример 1. Однопродуктовая модель оптимального развития экономики. Обозначим через X количество валового объема продукции, производимого в единицу времени (интенсивность выпуска валовой продукции), через C – интенсивность потребления. Однопродуктовая динамическая макроэкономическая модель Леонтьева представляет собой балансовое соотношение

                                     X=aX+b 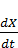+C.                                     (3.1)

Соотношение (3.1) показывает, как валовая продукция X распадается на три составляющие. Первая составляющая, aX – это производственные затраты, которые пропорциональны выпуску продукции X ( a – коэффициент производственных материальных затрат). Вторая составляющая, 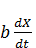– прирост основных производственных фондов. В этой модели предполагается, что амортизационные отчисления отсутствуют, и все валовые капитальные вложения идут на ввод в действие новых основных производственных фондов. При этом считается, что капиталовложения пропорциональны приросту выпуска продукции в данном году (b – коэффициент приростной фондоемкости). Третья составляющая, C, – это непроизводственное потребление.                                                                                                                                                                                                                                         Предположим, что рассматривается развитие экономики на отрезке времени от  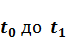(например, 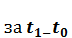лет). Согласно. (3.1), при каждом значении t экономический процесс на макроуровне может быть описан уравнением

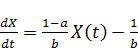                                  C(t)                                (3.2)

Это обыкновенное дифференциальное уравнение относительно X(t) . Так как количество производимой продукции определяется потреблением, то непроизводственное потребление можно считать движущей силой экономического процесса. Перенося это на язык математики, можно сказать, что в уравнении (3.2) C(t) – это управление, a X(t) -состояние экономической системы. Естественно предположить, что известно начальное состояние системы, то есть интенсивность валового выпуска в начальный момент времени. Переменные состояния X(t) в этой системе конечно же, неотрицательны, а величина потребления C(t) может изменяться только в каких-то определенных границах. Таким образом, имеем следующие ограничения для управляемого процесса (3.1.2):

                              X( 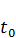) = 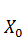.                                                       (3.3)

                             X(t) ≥ 0, t 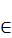[ 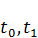],                                          (3.4)

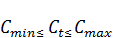                             , t 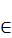[ 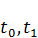].                            (3.5)  

Рассматриваемый процесс управления должен быть организован так, чтобы потребление было как можно больше, и в то же время в конечный момент времени должна быть высокой интенсивность выпуска продукции, что означает накопление производственного потенциала. Критерий качества процесса, предусматривающий эти требования, может быть выражен функционалом вида

         J(X(t),C(t))=a 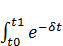 C(t)dt+βX( 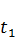)  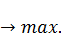                    (3.6)   

Здесь первое слагаемое – это суммарное взвешенное потребление на промежутке [ 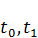]; второе слагаемое – интенсивность выпуска в конечный момент времени, α,β - весовые коэффициенты. Если предпочтение отдается потреблению, то α> β, а если предпочтение отдается накоплению производственного потенциала, то α<β. Подынтегральное выражение  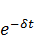C(t) – дисконтированное потребление,  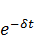– взвешивающая функция,  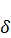– коэффициент дисконтирования. Таким образом, мы рассмотрели экономическую задачу управления процессом распределения валового продукта, моделью которой служит однопродуктовая динамическая макроэкономическая модель Леонтьева. Если при этом ставится цель роста потребления и наращивания экономического потенциала, то эта задача становится задачей оптимального управления Полученная задача оптимального управления состоит в нахождении состояния X(t) и управления C(t), которые удовлетворяют уравнению (3.2), условиям (3.3) – (3.5) и доставляют максимум функционалу (3.6).                                                          

Пример 2. Оптимальное распределение капитальных вложений в отрасли. Обозначим через K(t) величину основных производственных фондов в году t . Если проследить их изменение за промежуток времени Δt , то величина ΔK прироста основных производственных фондов за этот промежуток будет равна

                                          ΔK=K(t+ Δt)- K(t).

Рост основных производственных фондов происходит за счет капитальных вложений. Однако за счет физического и морального износа количество их уменьшается с течением времени. Обозначим через V(t) интенсивность ввода основных производственных фондов, т. е. количество вводимых фондов за единицу времени, например за год. Будем считать, что величина выбытия фондов в году t пропорциональна K(t) и равна 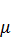 K(t), то есть величина  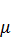K(t) – это интенсивность выбытия основных производственных фондов. Так как мы рассматриваем промежуток времени Δt , то за этот промежуток времени будет введено V(t)Δt единиц новых фондов, а количество выводимых из производства фондов составит  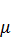K(t)Δt единиц. Таким образом, уравнение баланса основных производственных фондов будет иметь вид:

                        K(t+ Δt)- K(t)= V(t)Δt - 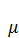 K(t)Δt.                                                  

Поделим обе части этого равенства на Δt и устремим Δt к 0. Получим:

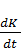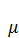                                     = -  K(t)+ V(t).                                    (3.7)

Обыкновенное дифференциальное уравнение (3.7) является моделью роста основных производственных фондов отрасли. Этот экономический процесс можно рассматривать как управляемый, если считать V(t) управлением, K(t) состоянием. На переменные состояния и управления следует наложить естественные ограничения:

                           K( 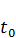) = 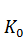.                                                             (3.8)

                          K(t) ≥ 0, t 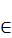[ 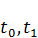],                                                (3.9)

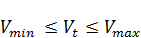                          , t 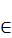[ 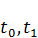].                            (3.10)  

где 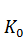– заданное начальное значение основных фондов,  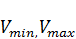                                               , – известные постоянные, или зависящие от времени функции. Для оценки протекающего процесса введем в рассмотрение критерий качества:                                                                                                        

                            F ( K ( t ), V ( t ))= α 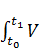( t ) dt - βK  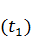                     (3.11)

Теперь можно сформулировать задачу оптимального управления: требуется найти пару V( t ),K( t ) , которая удовлетворяет уравнению (3.7), условиям (3.8) – (3.10) и доставляет минимум критерию качества (3.11). Так как функционал F состоит из двух слагаемых, то его минимизация означает, во-первых, экономию капиталовложений а во-вторых, максимизацию K( 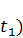 основных фондов в конце рассматриваемого отрезка времени (так как второе слагаемое входит со знаком минус). Числа α,β – это весовые коэффициенты, α <0, β>0. Если β < |α|, то приоритет отдается первому требованию, если |α| < β – то второму.

Пример 3 [2]. Оптимальное распределение капитальных вложений между отраслями. Этот пример обобщает пример 2 на случай нескольких отраслей. Рассматривается процесс распределения основных производственных фондов между отраслями в течение некоторого промежутка времени. Пусть имеется n отраслей. Обозначим через 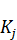 (t) величину основных фондов j -й отрасли в году t ,  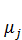– коэффициент ежегодного выбытия фондов в j -й отрасли,  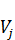(t) – величину вводимых в действие в году t основных фондов в j -й отрасли. Аналогично предыдущему примеру можно вывести уравнение баланса основных фондов для каждой отрасли:

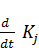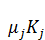                           (t) = - (t)+ 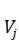 (t),  j=1,…,n, t 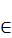[ 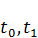]. (3.12)

В результате мы получим систему дифференциальных уравнений как модель изучаемого экономического процесса. В этой системе

V ( t )= 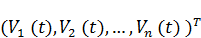 – вектор управления, K ( t )=  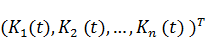 – вектор состояния.

Должны быть известны основные фонды отраслей в начале исследуемого промежутка времени:

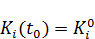                       , i =1,…., n .                                (3.13)

Переменные управления и переменные состояния должны быть неотрицательны:

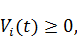
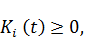                        i=1,….,n, t 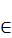[ 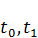]. (3.14)

Суммарная величина вводимых в действие основных фондов должна быть ограничена:

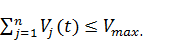                                                                     (3.15)

Критерий качества в данном случае будет иметь вид:

         F(K(t),V(t))=  –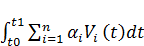    

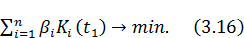
Итак, задачу оптимального распределения капиталовложений между отраслями можно сформулировать как задачу оптимального управления для системы (3.12) при ограничениях (3.13) – (3.15) с критерием качества (3.16). 

                                            Заключение

Для изучения влияния управленческих решений на функционирование, сохранение и развитие производственных систем необходимо рассматривать систему как единое целое, характеризующееся входящими в нее элементами и их взаимосвязями, объединенное общностью целей и особым единством со средой. Подход к анализу производственных систем и влияния на них управленческих решений разрабатывается с единых методологических позиций при рассмотрении теории систем как совокупности различных моделей и способов их описания. С этой целью используются принципы системного подхода экономическая система как некоторые аспекты математического моделирования. При таком подходе проблема рассматривается в целом, и поведение объекта изучают, абстрагируясь от его внутреннего устройства.

В курсовой работе рассмотрены задачи оптимального управления системами экономической динамики. Формулируются и подробно обсуждаются математические модели управляемых экономических систем, например, динамические модели односекторной и многосекторной экономики, а также некоторые другие задачи экономического содержания.

Литература

1. Лагоша Б. А. Оптимальное управление в экономике / Б. А. Лагоша. – М.: изд-во Московского государственного университета экономики, статистики и информатики, 2004.

2. Суровцов Л. К. Многоотраслевая модель экономической динамики с постоянными коэффициентами затрат, выпуска и распределения доходов / Л. К. Суровцов // Вестник Санкт-Петербургского университета. Экономика. – 2011. – №3. – С. 125-136.

3. Дужински Р. Р. Системные проблемы экономического роста в современной России / Р. Р. Дужински, Е. Л. Торопцевь, А. С. Мараховский // Экономический анализ: теория и практика. – 2017. – Т. 16, вып. 2. – С. 204-220.

4. Тырсин А. Н. Оптимизационное моделирование как инструмент управления экономической безопасностью региона / А. Н. Тырсин, Н. Л. Никулина, М. С. Печеркина // Вестник Бурятского государственного университета. Экономика и менеджмент. – 2018. – №4. – С. 99-107.

5. Колмакова А. И. Многометодная оптимизация управления в экономической модели выбора налоговой ставки для предприятий энергетической отрасли / А. И. Колмакова // Вестник Бурятского государственного университета. Математика, информатика. – 2013. – №9. – С. 3-11.

6. Кислицын Е. В. Аналитическое и имитационное моделирование экономических систем как средство формирования социально-ориентированной экономики в России / Е. В. Кислицын // Экономические исследования. – 2014. – №4. – С. 2-15.