МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«КЕМЕРОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Институт фундаментальных наук
Кафедра прикладной математики
КУРСОВАЯ РАБОТА
на тему «Моделирование экономической динамики в форме задачи оптимального управления»
по дисциплине «Теория оптимальных процессов»
студента 3 курса
Файзуллоева Кароматуллоха Абдунабиевича
Направление подготовки 01.03.02 Прикладная математика и информатика
Научный руководитель:
к.ф.-м.н., доцент
Мешечкин В.В.
| Работа защищена: | |
| “____”_________________2019 г. | |
| с оценкой ___________________ | |
Кемерово 2019
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ……………………………………………………………………………... 3
ГЛАВА 1. Основы моделирования экономических процессов
1.1.Система,модель...................................................................................... 5
1.2.Управление.Обратнаясвязь................................................................... 8
1.2.1.Общаяпринципиальнаясхемауправления.....................................… 9
1.2.2. Иерархия управления ..................................................................... 10
1.3. Экономическая система как объект управления (некоторые аспекты математического моделирования) .......................................................... 11
1.4 Роль моделей в экономической теории и принятии решений…….13
1.5 Этапы экономико-математического моделирования…………….. 13
ГЛАВА 2. Оптимизационные модели экономической динамики 2.1.Однопродуктовая динамическая макроэкономическая модель......15 2.2.Частные случаи....................................................................................17 2.3.Однопродуктовая оптимизационная динамическая макроэкономическая модель ........................................................................................................19
Глава 3.Практическая часть(примеры решения задач на тему моделирование экономической динамики в форме задачи оптимального управления)………………………………………………………………20
Заключение……………………………………………………………….24
Литература………………………………………………………………..25
Введение
В курсовой работе рассматриваются задачи экономической динамики в форме оптимального управления. По мере развития рыночной экономики в ней возросла роль математики как аналитического средства. Стало очевидным, что бизнес будет платить (и уже во многих случаях платит) за обоснованные компетентными расчетами и анализом инвестиционные проекты, прогнозы, рекомендации по снижению риска. В этих условиях экономика начала поворачиваться к естественно-научным дисциплинам, хотя ее достижения в этом направлении по-прежнему нельзя сопоставлять с точными законами и выводами в естествознании. Поэтому различные разделы математики, такие как теория оптимального управления (ТОУ), оказались нужны не только для инженеров, математиков, физиков и других представителей естественно-научных знаний, но и для экономистов. Теория оптимального управления инвариантна к прикладным областям применения, если содержательные постановки задач вписываются в рамки принятых в ней канонических правил. Соответствующие возможности в сфере экономики реализуются в форме динамических оптимизационных моделей в управляемых системах с различными целевыми функциями и множеством ограничений на переменные состояния и управления.
Оптимальное управление — это задача проектирования системы, обеспечивающей для заданного объекта управления или процесса закон управления или управляющую последовательность воздействий, обеспечивающих максимум или минимум заданной совокупности критериев качества системы. Задача оптимального управления включает в себя расчет оптимальной программы управления и синтез системы оптимального управления. Оптимальные программы управления, как правило, рассчитываются численными методами нахождения экстремума функционала или решения краевой задачи для системы дифференциальных уравнений. Синтез систем оптимального управления с математической точки зрения представляет собой задачу нелинейного программирования в функциональных пространствах.
Для решения задачи определения программы оптимального управления строится математическая модель управляемого объекта или процесса, описывающая его поведение с течением времени под влиянием управляющих воздействий и собственного текущего состояния. Если математическая модель управляемого объекта или процесса заранее неизвестна, то для её определения необходимо провести процедуру идентификации управляемого объекта или процесса
Математическая модель для задачи оптимального управления включает в себя: формулировку цели управления, выраженную через критерий качества управления; определение дифференциальных или разностных уравнений, описывающих возможные способы движения объекта управления; определение ограничений на используемые ресурсы в виде уравнений или неравенств. Все задачи оптимального управления можно рассматривать как задачи математического программирования и в таком виде решать их численными методами.
При оптимальном управлении иерархическими многоуровневыми системами, например, крупными химическими производствами, металлургическими и энергетическими комплексами, применяются многоцелевые и многоуровневые иерархические системы оптимального управления. В математическую модель вводятся критерии качества управления для каждого уровня управления и для всей системы в целом, а также координация действий между уровнями управления.
Если управляемый объект или процесс является детерминированным, то для его описания используются дифференциальные уравнения. Наиболее часто используются обыкновенные дифференциальные уравнения. В более сложных математических моделях (для систем с распределёнными параметрами) для описания объекта используются дифференциальные уравнения в частных производных. Если управляемый объект является стохастическим, то для его описания используются стохастические дифференциальные уравнения. Если решение поставленной задачи оптимального управления не является непрерывно зависящим от исходных данных (некорректная задача), то такая задача решается специальными численными методами.
Для решения задач оптимального управления с неполной исходной информацией и при наличии ошибок измерений используется метод максимального правдоподобия. Система оптимального управления, способная накапливать опыт и улучшать на этой основе свою работу, называется обучающейся системой оптимального управления. Реальное поведение объекта или системы всегда отличается от программного вследствие неточности в начальных условиях, неполной информации о внешних возмущениях, действующих на объект, неточности реализации программного управления и т. д. Поэтому для минимизации отклонения поведения объекта от оптимального обычно используется система автоматического регулирования.
Иногда (например, при управлении сложными объектами, такими как доменная печь в металлургии или при анализе экономической информации) в исходных данных и знаниях об управляемом объекте при постановке задачи оптимального управления содержится неопределённая или нечёткая информация, которая не может быть обработана традиционными количественными методами. В таких случаях можно использовать алгоритмы оптимального управления на основе математической теории нечётких множеств (нечёткое управление). Используемые понятия и знания преобразуются в нечёткую форму, определяются нечёткие правила вывода принимаемых решений, затем производится обратное преобразование нечётких принятых решений в физические управляющие переменные.
ГЛАВА 1. [1] Основы моделирования экономических процессов
Система, модель
Объектами применения ТОУ являются управляемые системы, описываемые дифференциальными или конечно-разностными уравнениями соответственно для непрерывных или дискретных (многошаговых) процессов. Понятия и определения: система, модель, обратная связь, внешняя среда, замкнутая и разомкнутая система, существенные или несущественные факторы, обусловленные целевой ориентацией при изучении объекта исследования, – это понятийный аппарат основ управления, и в частности, ТОУ. Так как речь идет именно об общих принципах и понятиях, то и примеры заимствуются из различных областей, начиная с физического движения материальной точки и кончая характеристиками сложных производственно-экономических систем. Наблюдение, анализ и моделирование являются средствами познания и прогнозирования процессов, явлений и ситуаций во всех сферах объективной действительности. Говоря, например, о системах застройки города или района, кровообращения, управления предприятием, системе уравнений, прежде всего имеют в виду некую совокупность. Но любая ли совокупность может быть названа системой? Вряд ли кто назовет системами совокупность выброшенных старых вещей или луж на асфальте после дождя. Ни то, ни другое никак не упорядочено, не отвечает определенной цели, в соответствии с которой эта совокупность сформирована. Первое свойство систематизации, системного представления о рассматриваемом объекте – это наличие цели, для реализации которой предназначается данная совокупность предметов, явлений, логических представлений, формирующих объект.
Цель функционирования системы редуцирует системные признаки, с помощью которых описываются, характеризуются элементы системы. Например, допустим, что целью является реструктуризация системы управления предприятием (фирмой) на ординарном уровне. Нужно ли для этого знать фамилии и размеры зарплаты каждого работника? Нет, так как эти данные хотя в своей совокупности в большей или меньшей степени влияют на режим управления, но не являются наиболее важными на персональном уровне. Выделим существенные системные признаки. К ним относятся: рыночный спрос на продукцию производителя и число наименований выпускаемой продукции, производственные мощности предприятия по выпуску продукции различных наименований и аналогичные показатели предприятий-конкурентов, обеспеченность материальными, трудовыми ресурсами, общий фонд заработной платы и условия ее использования и т.д. Особо следует выделить “узкие места”. К ним относятся факторы и условия, сдерживающие повышение эффективности производства.
Сущностью системы управления предприятием, отражения условий управляемости последним является установление и описание взаимосвязей и взаимозависимостей между наиболее существенными факторами и характеристиками предприятия. Еще раз подчеркнем, что речь идет о предприятии (фирме) как производственно-экономической системе с позиций управляемости, т.е. предприятие рассматривается как объект управления. Именно исходя из этого и определены существенные признаки объекта. При изменении цели могут стать другими как существенные признаки, так и связи с внешней средой. Например, если на том же предприятии будут анализироваться уровень квалификации работников и организация оплаты их труда, то ведомость на получение заработной платы, ранее не представлявшая первостепенного значения, станет теперь основным документом. Таким образом, для выделения системы требуется наличие:
а) цели, для реализации которой формируется система; б) объекта исследования, состоящего из множества элементов, связанных в единое целое важными относительно цели системными признаками; в) субъекта исследования (“наблюдателя”), формирующего систему; г) характеристик внешней среды по отношению к системе.
Наличие субъекта исследования и возможная неоднозначность, субъективность при выделении существенных системных признаков вызывают значительные трудности в процессе выделения системы и соответственно ее универсального определения. Поэтому необходим более подробный системный анализ. Изложенный выше вербальный подход дает возможность определить систему как упорядоченное представление об объекте исследования относительно поставленной цели. Упорядоченность заключается в целенаправленном выделении системообразующих элементов, установлении их существенных признаков, характеристик взаимосвязей между собой и с внешней средой. Системный подход, формирование систем позволяют выделить главное, наиболее существенное в исследуемых объектах и явлениях; игнорирование второстепенного упрощает, упорядочивает в целом изучаемые процессы. Для анализа многих сложных ситуаций такой подход важен сам по себе, однако, как правило, построение системы служит предпосылкой для разработки или реализации модели конкретной ситуации. Описанный подход предполагает ясность цели исследования и детерминированное к ней отношение всех элементов системы, взаимосвязь между ними и с внешней средой. Такие системы называют детерминированными. Это не означает, что все предпосылки, лежащие в основе их построения, на практике выполняются.
Однако во многих случаях, и это характерно для экономики, цель исследований – изучение и анализ природы усредненных и устойчивых в среднем показателей. Это определяет детерминированный подход к построению системы. Перейдем к рассмотрению сущности понятий модель и моделирование. Слово “модель” (фр. “modele”) имеет несколько значений: образцовый экземпляр какого-либо изделия; вид, тип конструкции (например, автомобиля); материал, натура для художественного произведения; копия, воспроизведение предмета, обычно в уменьшенном размере; исследуемый объект, представленный в наиболее общем виде.
В качестве примеров моделей можно привести глобус как модель земного шара, карту как модель местности, маленькую, например, настольную модель самолета, внешне подобную своему натуральному образцу, и т.д. Однако, по настольной модели самолета нельзя определить его прочностные, аэродинамические характеристики, характеристики системы управления. Следовательно, для реализации названных целей данная модель не годится. Эта модель подошла бы, если бы наша цель была – добиться внешнего подобия. Таким образом, и это главное, структура и свойства модели зависят от целей, для достижения которых она создается. В этом органическое единство системы и модели. Если неизвестна цель моделирования, то неизвестно и с учетом каких свойств и качеств надо строить модель.
Следовательно, модель – это формализованное представление об объекте исследования относительно поставленной цели. Модели можно различать по характеру моделируемых объектов, сферам приложения, глубине моделирования. В зависимости от средств моделирования выделяются материальное (предметное) и идеальное моделирование. Материальное моделирование, основывающееся на материальной аналогии моделируемого объекта и модели, осуществляется путем воспроизведения основных геометрических, физических, других функциональных характеристик изучаемого объекта. Частным случаем материального моделирования является физическое моделирование, по отношению к которому, в свою очередь, частным случаем является аналоговое моделирование. Оно основано на аналогии явлений, имеющих различную физическую природу, но описываемых одинаковыми математическими соотношениями. Пример аналогового моделирования – изучение механических колебаний с помощью электрической системы, описываемой теми же дифференциальными уравнениями. Так как эксперименты с электрической системой обычно проще и дешевле, она исследуется в качестве аналога механической системы (например, при изучении колебаний мостов). Идеальное моделирование отличается от материального принципиально. Оно основано на идеальной, или мыслимой, аналогии. В экономических исследованиях это основной вид моделирования. Идеальное моделирование, в свою очередь, разбивается на два подкласса: знаковое (формализованное) и интуитивное моделирование. При знаковом моделировании моделями служат схемы, графики, чертежи, формулы. Важнейшим видом знакового моделирования является математическое моделирование, осуществляемое средствами логико-математических построений. Интуитивное моделирование (например, рисковых ситуаций ) встречается в тех областях науки, где познавательный процесс находится на начальной стадии или имеют место очень сложные взаимосвязи. Такие исследования называют мысленными экспериментами. В экономике в основном применяется интуитивное моделирование; оно описывает практический опыт исполнителей и руководящих работников.
Иерархия управления
Представленное описание замкнутой системы управления весьма схематично и отражает только принцип ее построения. В действительности каждый из указанных элементов, в свою очередь, может включать объект, субъект управления с обратной связью или без нее, вся система будет иметь, таким образом, иерархическую структуру. Подобное характерно для экономических систем прежде всего. Например, в системе управления крупной фирмой отраслевого профиля (например, автомобильный или нефтяной гигант) в качестве объекта управления рассматривают подведомственные фирмы и дочерние предприятия, а управляющего органа – центральный аппарат. Обратная связь при этом осуществляется через систему учета, контроля и оперативного управления в отношении подведомственных предприятий. Каждое предприятие, являясь, таким образом, объектом управления, в свою очередь, представляет замкнутую систему под воздействием внешней среды – вышестоящего уровня управления со всеми необходимыми структурными элементами.
Объект управления – цехи, производственные участки; управляющая система – дирекция предприятия со своими службами; обратная связь осуществляется также через систему учета, контроля и оперативного управления со стороны руководства предприятия. Если спускаться по этой иерархической лестнице, то по аналогичной схеме можно рассмотреть систему управления цехом. В рамках крупных производственных комплексов (возможно, и международного уровня) такие иерархические структуры могут быть многоступенчатыми.
Частные случаи.
С л у ч а й 1. Открытая однопродуктовая динамическая модель Леонтьева. Предполагают, что все валовые инвестиции идут на ввод в действие новых основных производственных фондов (основные фонды не изнашиваются). Считая, что прирост выпуска продукции Δ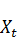 
= 
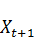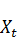- пропорционален капитальным вложениям, т.е.
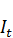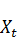= η Δ , (2.7)
из уравнений (2.1), (2.2), с учетом выражений (2.5), (2.7), получим однопродуктовую открытую динамическую модель Леонтьева:
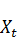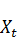= a + η Δ +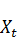 
.
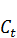В непрерывном варианте однопродуктовая динамическая макромодель Леонтьева имеет вид:
X = aX + η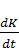 
+ C. (2.8)
C математической точки зрения эта модель представляет линейное неоднородное дифференциальное уравнение первого порядка (при решении уравнений второго порядка первый порядок может рассматриваться как частный случай).
С л у ч а й 2. Замкнутая однопродуктовая модель Леонтьева. Предполагают, что непроизводственное потребление C(t) идет полностью на восстановление рабочей силы L(t). Тогда, введя норму потребления γ (t), получим
C(t) = γ (t) L(t). (2.9) Далее, если считать, что затраты труда пропорциональны выпуску продукции, то
L(t) = b(t) X(t), (2.10)
где b(t) - норма трудоемкости.
Подставляя в формулу (2.8) соотношения (2.9) и (2.10), получим “замкнутую по потреблению” модель расширенного воспроизводства
X(t) = a(t) X(t) + η(t) 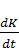+ γ (t) b(t) X(t),
которая описывается однородным дифференциальным уравнением первого порядка с разделяющимися переменными
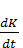- p(t) X(t) = 0, (2.10’)
p(t) = [1 - a(t) - γ (t) b(t)]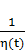 
Тогда развитие экономики определяется решением уравнения (2.10):
X(t) =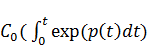 
С л у ч а й 3. Непроизводственное потребление является известной функцией времени. При этом закон развития экономики определяется из модели (2.8), которая представляет из себя неоднородное дифференциальное уравнение первого порядка:
+ 
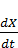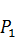(t) X(t) = f(t),
( t )=-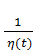 
[1 - a(t)]; f ( t )= - 
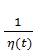C ( t ), с решением
X(t) = exp(-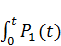 
dt)[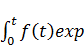 
(- 
)+ 
].
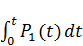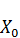Итак, выделение из конечного продукта Y накапливаемой части I приводит к рассмотрению динамических моделей и применению для их исследования в качестве математического инструментария теории дифференциальных (в непрерывном случае) и конечноразностных (в многошаговом варианте) уравнений.
Примеры задач оптимального управления экономическими системами
Пример 1. Однопродуктовая модель оптимального развития экономики. Обозначим через X количество валового объема продукции, производимого в единицу времени (интенсивность выпуска валовой продукции), через C – интенсивность потребления. Однопродуктовая динамическая макроэкономическая модель Леонтьева представляет собой балансовое соотношение
X=aX+b 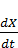+C. (3.1)
Соотношение (3.1) показывает, как валовая продукция X распадается на три составляющие. Первая составляющая, aX – это производственные затраты, которые пропорциональны выпуску продукции X ( a – коэффициент производственных материальных затрат). Вторая составляющая,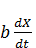 
– прирост основных производственных фондов. В этой модели предполагается, что амортизационные отчисления отсутствуют, и все валовые капитальные вложения идут на ввод в действие новых основных производственных фондов. При этом считается, что капиталовложения пропорциональны приросту выпуска продукции в данном году (b – коэффициент приростной фондоемкости). Третья составляющая, C, – это непроизводственное потребление. Предположим, что рассматривается развитие экономики на отрезке времени от 
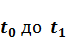(например, 
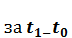лет). Согласно. (3.1), при каждом значении t экономический процесс на макроуровне может быть описан уравнением
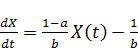C(t) (3.2)
Это обыкновенное дифференциальное уравнение относительно X(t) . Так как количество производимой продукции определяется потреблением, то непроизводственное потребление можно считать движущей силой экономического процесса. Перенося это на язык математики, можно сказать, что в уравнении (3.2) C(t) – это управление, a X(t) -состояние экономической системы. Естественно предположить, что известно начальное состояние системы, то есть интенсивность валового выпуска в начальный момент времени. Переменные состояния X(t) в этой системе конечно же, неотрицательны, а величина потребления C(t) может изменяться только в каких-то определенных границах. Таким образом, имеем следующие ограничения для управляемого процесса (3.1.2):
X(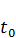 
) = 
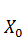. (3.3)
X(t) ≥ 0, t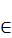 
[ 
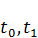], (3.4)
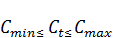, t 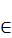[ 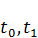]. (3.5)
Рассматриваемый процесс управления должен быть организован так, чтобы потребление было как можно больше, и в то же время в конечный момент времени должна быть высокой интенсивность выпуска продукции, что означает накопление производственного потенциала. Критерий качества процесса, предусматривающий эти требования, может быть выражен функционалом вида
J(X(t),C(t))=a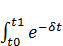 
C(t)dt+βX( 
) 
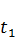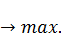(3.6)
Здесь первое слагаемое – это суммарное взвешенное потребление на промежутке [ 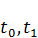]; второе слагаемое – интенсивность выпуска в конечный момент времени, α,β - весовые коэффициенты. Если предпочтение отдается потреблению, то α> β, а если предпочтение отдается накоплению производственного потенциала, то α<β. Подынтегральное выражение 
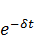C(t) – дисконтированное потребление, 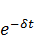– взвешивающая функция, 
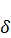– коэффициент дисконтирования. Таким образом, мы рассмотрели экономическую задачу управления процессом распределения валового продукта, моделью которой служит однопродуктовая динамическая макроэкономическая модель Леонтьева. Если при этом ставится цель роста потребления и наращивания экономического потенциала, то эта задача становится задачей оптимального управления Полученная задача оптимального управления состоит в нахождении состояния X(t) и управления C(t), которые удовлетворяют уравнению (3.2), условиям (3.3) – (3.5) и доставляют максимум функционалу (3.6).
Пример 2. Оптимальное распределение капитальных вложений в отрасли. Обозначим через K(t) величину основных производственных фондов в году t . Если проследить их изменение за промежуток времени Δt , то величина ΔK прироста основных производственных фондов за этот промежуток будет равна
ΔK=K(t+ Δt)- K(t).
Рост основных производственных фондов происходит за счет капитальных вложений. Однако за счет физического и морального износа количество их уменьшается с течением времени. Обозначим через V(t) интенсивность ввода основных производственных фондов, т. е. количество вводимых фондов за единицу времени, например за год. Будем считать, что величина выбытия фондов в году t пропорциональна K(t) и равна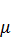 
K(t), то есть величина 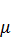K(t) – это интенсивность выбытия основных производственных фондов. Так как мы рассматриваем промежуток времени Δt , то за этот промежуток времени будет введено V(t)Δt единиц новых фондов, а количество выводимых из производства фондов составит 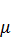K(t)Δt единиц. Таким образом, уравнение баланса основных производственных фондов будет иметь вид:
K(t+ Δt)- K(t)= V(t)Δt -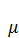 
K(t)Δt.
Поделим обе части этого равенства на Δt и устремим Δt к 0. Получим:
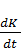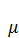= - K(t)+ V(t). (3.7)
Обыкновенное дифференциальное уравнение (3.7) является моделью роста основных производственных фондов отрасли. Этот экономический процесс можно рассматривать как управляемый, если считать V(t) управлением, K(t) состоянием. На переменные состояния и управления следует наложить естественные ограничения:
K( ) =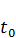 
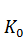. (3.8)
K(t) ≥ 0, t 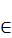[ 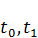], (3.9)
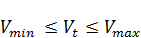, t 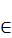[ 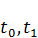]. (3.10)
где 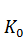– заданное начальное значение основных фондов, 
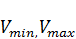, – известные постоянные, или зависящие от времени функции. Для оценки протекающего процесса введем в рассмотрение критерий качества:
F ( K ( t ), V ( t ))= α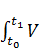 
( t ) dt - βK 
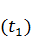(3.11)
Теперь можно сформулировать задачу оптимального управления: требуется найти пару V( t ),K( t ) , которая удовлетворяет уравнению (3.7), условиям (3.8) – (3.10) и доставляет минимум критерию качества (3.11). Так как функционал F состоит из двух слагаемых, то его минимизация означает, во-первых, экономию капиталовложений а во-вторых, максимизацию K(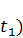 
основных фондов в конце рассматриваемого отрезка времени (так как второе слагаемое входит со знаком минус). Числа α,β – это весовые коэффициенты, α <0, β>0. Если β < |α|, то приоритет отдается первому требованию, если |α| < β – то второму.
Пример 3 [2]. Оптимальное распределение капитальных вложений между отраслями. Этот пример обобщает пример 2 на случай нескольких отраслей. Рассматривается процесс распределения основных производственных фондов между отраслями в течение некоторого промежутка времени. Пусть имеется n отраслей. Обозначим через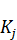 
(t) величину основных фондов j -й отрасли в году t , 
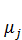– коэффициент ежегодного выбытия фондов в j -й отрасли, 
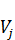(t) – величину вводимых в действие в году t основных фондов в j -й отрасли. Аналогично предыдущему примеру можно вывести уравнение баланса основных фондов для каждой отрасли:
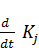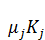(t) = - 
(t)+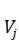 
(t), j=1,…,n, t 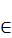[ 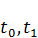]. (3.12)
В результате мы получим систему дифференциальных уравнений как модель изучаемого экономического процесса. В этой системе
V ( t )=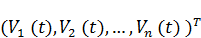 
– вектор управления, K ( t )= 
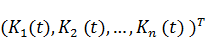– вектор состояния.
Должны быть известны основные фонды отраслей в начале исследуемого промежутка времени:
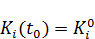, i =1,…., n . (3.13)
Переменные управления и переменные состояния должны быть неотрицательны:
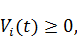
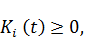i=1,….,n, t 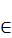[ 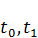]. (3.14)
Суммарная величина вводимых в действие основных фондов должна быть ограничена:
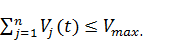(3.15)
Критерий качества в данном случае будет иметь вид:
F(K(t),V(t))=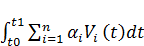 
– 
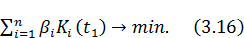
Итак, задачу оптимального распределения капиталовложений между отраслями можно сформулировать как задачу оптимального управления для системы (3.12) при ограничениях (3.13) – (3.15) с критерием качества (3.16).
Заключение
Для изучения влияния управленческих решений на функционирование, сохранение и развитие производственных систем необходимо рассматривать систему как единое целое, характеризующееся входящими в нее элементами и их взаимосвязями, объединенное общностью целей и особым единством со средой. Подход к анализу производственных систем и влияния на них управленческих решений разрабатывается с единых методологических позиций при рассмотрении теории систем как совокупности различных моделей и способов их описания. С этой целью используются принципы системного подхода экономическая система как некоторые аспекты математического моделирования. При таком подходе проблема рассматривается в целом, и поведение объекта изучают, абстрагируясь от его внутреннего устройства.
В курсовой работе рассмотрены задачи оптимального управления системами экономической динамики. Формулируются и подробно обсуждаются математические модели управляемых экономических систем, например, динамические модели односекторной и многосекторной экономики, а также некоторые другие задачи экономического содержания.
Литература
1. Лагоша Б. А. Оптимальное управление в экономике / Б. А. Лагоша. – М.: изд-во Московского государственного университета экономики, статистики и информатики, 2004.
2. Суровцов Л. К. Многоотраслевая модель экономической динамики с постоянными коэффициентами затрат, выпуска и распределения доходов / Л. К. Суровцов // Вестник Санкт-Петербургского университета. Экономика. – 2011. – №3. – С. 125-136.
3. Дужински Р. Р. Системные проблемы экономического роста в современной России / Р. Р. Дужински, Е. Л. Торопцевь, А. С. Мараховский // Экономический анализ: теория и практика. – 2017. – Т. 16, вып. 2. – С. 204-220.
4. Тырсин А. Н. Оптимизационное моделирование как инструмент управления экономической безопасностью региона / А. Н. Тырсин, Н. Л. Никулина, М. С. Печеркина // Вестник Бурятского государственного университета. Экономика и менеджмент. – 2018. – №4. – С. 99-107.
5. Колмакова А. И. Многометодная оптимизация управления в экономической модели выбора налоговой ставки для предприятий энергетической отрасли / А. И. Колмакова // Вестник Бурятского государственного университета. Математика, информатика. – 2013. – №9. – С. 3-11.
6. Кислицын Е. В. Аналитическое и имитационное моделирование экономических систем как средство формирования социально-ориентированной экономики в России / Е. В. Кислицын // Экономические исследования. – 2014. – №4. – С. 2-15.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«КЕМЕРОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Институт фундаментальных наук
Дата: 2019-05-29, просмотров: 199.
