Прежде чем переходить к построению абстрактных моделей управляемых процессов и, в частности, к моделям развития экономики рассмотрим механизм построения нескольких простых примеров экономической динамики. Исследование взаимосвязей элементов производства вне общественной формы реализации продукции приводит к производственно-технологической интерпретации экономики.

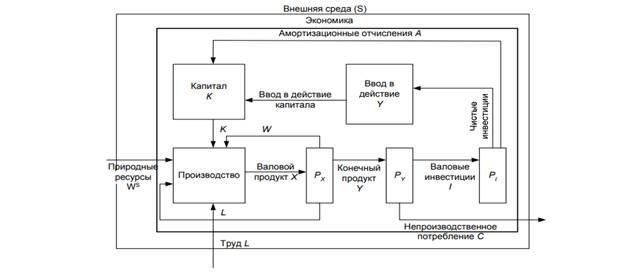
На представленной схеме выделены факторы, характеризующие производство: живой труд (L), средства труда (основные производственные фонды, капитал K) и предметы труда 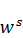 – ресурсы. Результатом производственной деятельности является валовой продукт (X), распределяемый в блоке 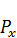на производственное потребление (W) и конечный продукт (Y). В свою очередь, конечный продукт (Y) делится в блоке распределения  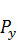на валовые капитальные вложения (I) и на непроизводственное потребление (C).   

Валовые капитальные вложения I, входящие в блок 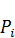, делятся на амортизационные отчисления A и чистые инвестиции, идущие на расширение производственных фондов. Ограничимся изучением взаимосвязей между синтетическими показателями верхнего уровня экономической иерархии. Одним из подходов к решению данной проблемы является построение однопродуктовой макроэкономической модели. С помощью этой модели изучают свойства и тенденции изменения взаимосвязанных агрегированных показателей, таких, как валовой и конечный продукты, трудовые ресурсы, производственные фонды (капитал), инвестиции, потребление и т.д. Так, на макроуровне блок распределения  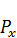показывает взаимосвязь между валовым продуктом X, производственным потреблением W и конечным продуктом Y:

                                                   X=W + Y.                                          (2.1) 

Блок P(Y) делит конечный продукт на две составляющие: валовые капитальные вложения I и непроизводственное потребление C, т.е.

                                                    Y= I + C.                                           (2.2)     

Инвестиции составляют материальную основу наращивания и перевооружения производства. За их счет осуществляется ввод в действие основных производственных фондов. Однако этот процесс сопряжен с определенными трудностями, одной из которых является учет распределенного запаздывания прироста основных фондов от реализации капитальных вложений. В экономико-математическом моделировании имеется ряд подходов к описанию этой взаимосвязи. В однопродуктовой модели делается предположение, что валовые инвестиции полностью расходуются на прирост основных производственных фондов, в том же году и на амортизационные отчисления:

а) в дискретном варианте эта взаимосвязь имеет вид:

                                  I = q Δ 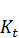 + A;                                                       (2.3) 

                                 Δ 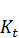=  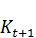-  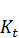; A = μ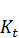  

где Δ 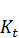– прирост основных производственных фондов в году t;                                                   q – параметр модели;                                                                                                                                             А – амортизационные отчисления;                                                                                                    μ – коэффициент амортизации;  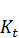                                                                                                              – основные производственные фонды в году t.

б) аналогом уравнения (2.3) в непрерывном варианте является

                                 I = q 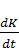 +μK.                                                         (2.3’)

 Отсюда можно получить дифференциальное уравнение динамики фондов                                                  

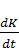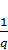                                =  (I - μK).                                                    (2.4)   

Объединяя уравнения связи (2.1) – (2.4), получим однопродуктовую динамическую макромодель в дискретном варианте:

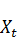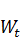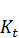                        = + q Δ  + μ  + .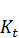

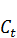Если считать производственные затраты W пропорциональными выпуску продукции X, т.е.      

                                                W = aX,                  (2.5)                                                                                                            то в дискретном варианте однопродуктовая динамическая модель примет вид:

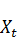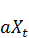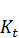                                = + q Δ  + μ 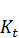 +  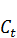                           (2.6)                     откуда можно получить Δ  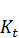=  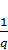[(1 - a)  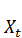- μ 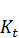–  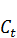], а в непрерывном варианте d 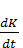=  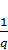[(1 - a ) X - μ K - C ]. В некоторых случаях используют упрощенные варианты однопродуктовой динамической модели. 

Частные случаи.                                                                                                                    

С л у ч а й 1. Открытая однопродуктовая динамическая модель Леонтьева. Предполагают, что все валовые инвестиции идут на ввод в действие новых основных производственных фондов (основные фонды не изнашиваются). Считая, что прирост выпуска продукции  Δ 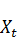= 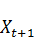-  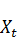пропорционален капитальным вложениям, т.е.                                                       

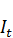                               = η Δ 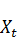 ,                                                           (2.7)

из уравнений (2.1), (2.2), с учетом выражений (2.5), (2.7), получим однопродуктовую открытую динамическую модель Леонтьева:

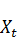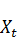                                  = a  + η Δ + .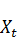

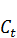 В непрерывном варианте однопродуктовая динамическая макромодель Леонтьева имеет вид:

                        X = aX + η 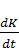 + C.                                                 (2.8)

C математической точки зрения эта модель представляет линейное неоднородное дифференциальное уравнение первого порядка (при решении уравнений второго порядка первый порядок может рассматриваться как частный случай).

С л у ч а й 2. Замкнутая однопродуктовая модель Леонтьева. Предполагают, что непроизводственное потребление C(t) идет полностью на восстановление рабочей силы L(t). Тогда, введя норму потребления γ (t), получим

                        C(t) = γ (t) L(t).                                                              (2.9)                 Далее, если считать, что затраты труда пропорциональны выпуску продукции, то            

                                  L(t) = b(t) X(t),                                                    (2.10)                                  

где b(t) - норма трудоемкости.

Подставляя в формулу (2.8) соотношения (2.9) и (2.10), получим “замкнутую по потреблению” модель расширенного воспроизводства                 

                                   X(t) = a(t) X(t) + η(t) 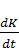+ γ (t) b(t) X(t),                                                      

которая описывается однородным дифференциальным уравнением первого порядка с разделяющимися переменными

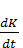                                 - p(t) X(t) = 0,                                                  (2.10’)                                  

                                 p(t) = [1 - a(t) - γ (t) b(t)]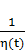                                                                          

Тогда развитие экономики определяется решением уравнения (2.10):

                               X(t) =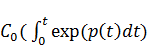         

С л у ч а й 3. Непроизводственное потребление является известной функцией времени. При этом закон развития экономики определяется из модели (2.8), которая представляет из себя неоднородное дифференциальное уравнение первого порядка:

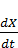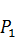                                + (t) X(t) = f(t),

( t )=- 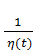  [1 - a(t)];  f ( t )= - 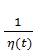C ( t ), с решением

                             X(t) = exp(- 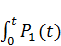dt)[ (- )+ ].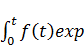

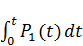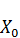Итак, выделение из конечного продукта Y накапливаемой части I приводит к рассмотрению динамических моделей и применению для их исследования в качестве математического инструментария теории дифференциальных (в непрерывном случае) и конечноразностных (в многошаговом варианте) уравнений.