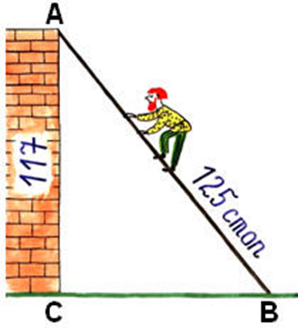
Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать.

Решение. По теореме Пифагора

,

,

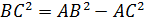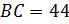 стоп.

Ответ: 44 стоп.

Задача кассирши.

Три монеты лежат на столе, касаясь друг друга, а их центры образуют прямоугольный треугольник. Приведите их размеры, выраженные наименьшими возможными целыми числами.

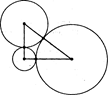Решение. Так как центры окружностей образуют прямоугольный треугольник, то для его сторон должна выполняться теорема Пифагора. Размеры должны быть наименьшими целыми числами, значит это – египетский треугольник со сторонами 3,4 и 5. Пусть радиус большей окружности равен 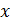, радиус средней окружности – 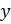, радиус меньшей окружности – 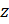. Получаем:

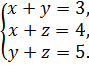
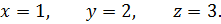
Ответ: 1, 2, 3.

Путь жука.

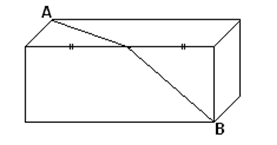У дороги лежит тесаный гранитный камень в 30см длины, 20 см высоты и такой же толщины. В точке А – жук, намеривающийся кратчайшим путем направиться к углу В. Как пролегает этот кратчайший путь и какой он длины?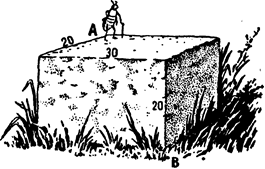

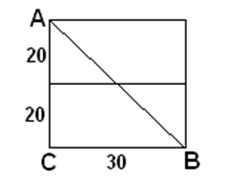Решение. Кратчайший путь легко определится, если мы мысленно повернем верхнюю грань камня так, чтобы она оказалась в одной плоскости с передней.

 Тогда АВ – кратчайший путь. АВ=50 см.

Ответ: 50 см.

10. Путешествие шмеля.

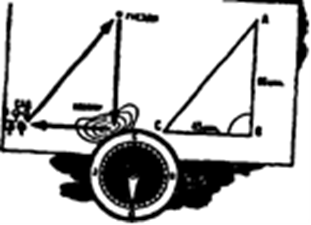
Шмель отправляется в дальнее путешествие. Из родного гнезда он летит прямо на юг, пересекает речку и, наконец, после целого часа пути спускается на косогор, покрытый душистым клевером. Здесь, перелетая с цветка на цветок, шмель остается полчаса. Теперь надо посетить сад, где шмель вчера заметил цветущие кусты крыжовника. Сад лежит на запад от косогора, и шмель спешит прямо туда. Спустя ¾  часа он был уже в саду. Крыжовник в полном цвету, и, чтобы посетить все кусты, понадобилось шмелю ½ часа. А затем, не отвлекаясь в стороны, шмель кратчайшей дорогой полетел домой, в родное гнездо. Сколько пробыл шмель в путешествии?

Решение. Найдем, сколько времени понадобилось шмель на перелет из сада в гнездо. Начертим путь шмеля. Мы знаем, что шмель летел сначала прямо на юг в течение 60 минут. Затем он летел 45 минут на запад, то есть под прямым углом к прежнему пути. Оттуда кратчайшей дорогой, то есть по прямой линии, обратно к гнезду.

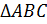 – прямоугольный.

По теореме Пифагора находим АС =75 мин = 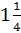 ч.

Ответ: 5 часов пробыл шмель в путешествии.

11.   Теорема Пифагора

Ученые собираются сложить из нанотрубок прямоугольный треугольник. Они планируют использовать 12 нанотрубок длиной 200 нм. Получится ли у них? Если да, каковы будут длины сторон прямоугольного треугольника? (Ответ обоснуйте.)

Решение. Да, получится. Например, они могут сложить треугольник со сторонами 3, 4 и 5 нанотрубок, то есть 3·200=600, 4·200=800 и 5·200=1000 нанометров.

Алгоритм решения задач по теореме Пифагора: