Палка длиной 1/2, прислонена к стене. Ее верхний конец опустили на 1/10. Как далеко отодвинется ее нижний конец?
Решение. В задаче по данным: гипотенузе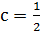 
и одному из катетов 
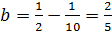необходимо найти второй катет. Его, как и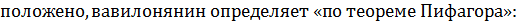 
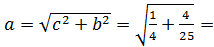3/10.
Ответ: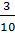 
.
Древнеиндийская задача.
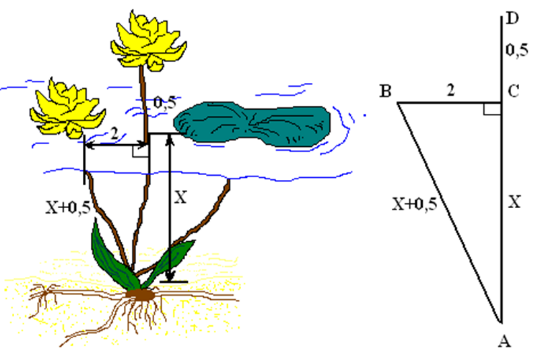Над озером тихим
С полфута размером
Высился лотоса цвет.
Он рос одиноко,
И ветер порывом
Отнес его в сторону. Нет
Боле цветка над водой.
Нашел же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак, предложу я вопрос:
«Как озера вода здесь глубока?»
Решение. Пусть глубина озера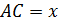 
, тогда 
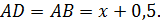Из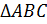 
по теореме Пифагора имеем 
,
,
,
.
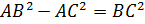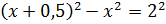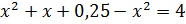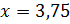Таким образом, глубина озера составляет 3,75 фута.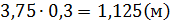 
.
Ответ: 3,75 фута или 1,125 м.
3. Задача индийского математика XII в. Бхаскары.
На берегу рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С течением реки его ствол составлял.
Запомни теперь, что в этом месте река
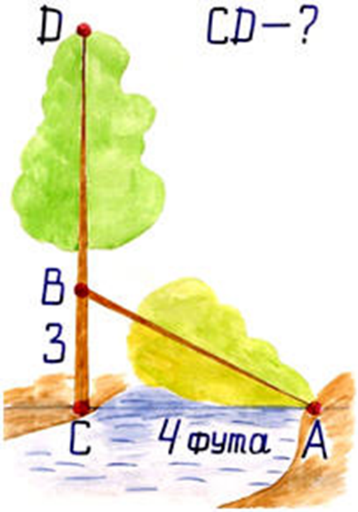В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?
Решение. По теореме Пифагора
,
,
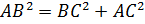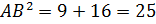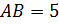(футов) длина отломленной части ствола.
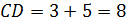(футов) высота ствола.
Ответ: 8 футов.
Задача о бамбуке из древнекитайского трактата
«Гоу-гу».
Имеется бамбук высотой в 1 чжан. Вершину его согнули так, что она касается земли на расстоянии 3 чи от корня ( 1 чжан = 10 чи). Какова высота бамбука после сгибания?
Решение. Пусть высота бамбука после сгибания равна х. По теореме Пифагора
,
,
,
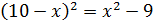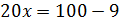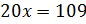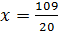=5,45 чи.
Ответ: 5,45 чи.
Задача арабского математика XI века.
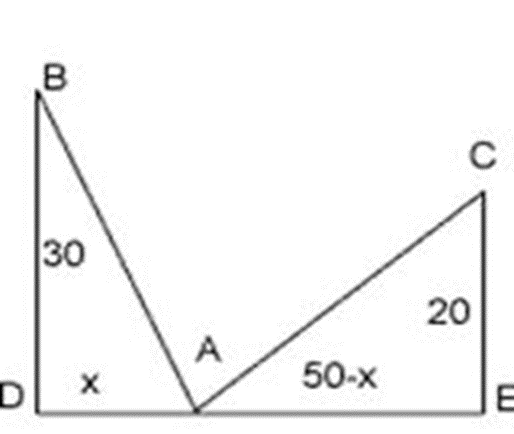На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой – 20 локтей. Расстояние между их основаниями – 5о локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли ее одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба?
Решение. В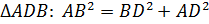 
,
,
.
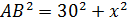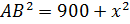В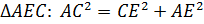 
,
,
,
.
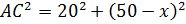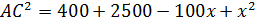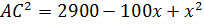Но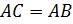 
, так как обе птицы пролетели эти расстояния за одинаковое время.
Поэтому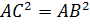 
,
,
,
,
.
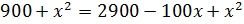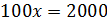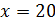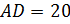Значит, рыба была на расстоянии 20 локтей от большей пальмы.
Ответ: 20 локтей.
Задача из китайской «Математики в девяти книгах».
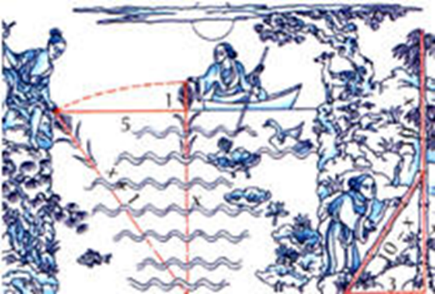Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснется его. Спрашивается: какова глубина воды, и какова длина камыша?
Решение.
По теореме Пифагора
,
,
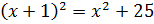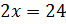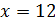чи.;
12+1=13 чи.
Ответ: глубина воды – 12 чи, длина камыша – 13 чи.
Дата: 2019-04-23, просмотров: 447.
