Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ТЕОРЕМА ПИФАГОРА

 В ЗАДАЧАХ РЕАЛЬНОЙ МАТЕМАТИКИ

 (сборник задач с практическим содержанием,

решаемых с помощью теоремы Пифагора)

 

Составители:

П. Е. Алдохина	- обучающаяся 10 А класса МБОУ «Золотухинская средняя общеобразовательная школа»
Е. А. Гоменюк	- обучающаяся 10 А класса МБОУ «Золотухинская средняя общеобразовательная школа»
Л. М. Семенихина	- учитель математики МБОУ «Золотухинская средняя общеобразовательная школа»

 

 

Алдохина П. Е., Гоменюк Е. А., Семенихина Л. М.

Теорема Пифагора в задачах реальной математики. Сборник задач с практическим содержанием, решаемых с помощью теоремы Пифагора, 2017г. – 30с.

Брошюра может быть использована в качестве дополнительного сборника задач при изучении геометрии в 8 -11-х классах, при организации обобщающего повторения в

9 – 11-х классах, в работе кружков, курсов по выбору или элективных курсов по математике, а также при подготовке к ОГЭ и ЕГЭ по математике.

 

 

ВВЕДЕНИЕ

    Теорема Пифагора по праву является одной из основных теорем математики. Значение этой теоремы заключается в том, что при ее помощи можно вывести большую часть теорем геометрии. Ценность ее в современном мире также велика, поскольку теорема Пифагора применяется во многих отраслях деятельности человека. Например, ее используют при расположении молниеотводов на крышах зданий, при производстве окон некоторых архитектурных стилей и даже при вычислении высоты антенн операторов мобильной связи. И это далеко не весь перечень практического применения данной теоремы. Вот почему очень важно знать теорему Пифагора и понимать ее практическое значение. С этой целью практические задачи, которые решаются с помощью теоремы Пифагора, включены в КИМы ОГЭ и ЕГЭ по математике.

    Данная брошюра содержит задачи с практическим содержанием, решаемые с помощью теоремы Пифагора, причем демонстрируется ее применение при решении задач в различных областях человеческой деятельности.

Книга разделена на 3 части.

Первая часть содержит исторические и занимательные задачи с решениями, найденные в различных источниках.

Во второй части собраны задачи из КИМов ОГЭ по математике. Предлагаемые задачи сопровождаются рисунками, позволяющими лучше понять условие, представить соответствующую геометрическую ситуацию, наметить план решения, при необходимости провести дополнительные построения и вычисления, а главное, увидеть связь современных реальных ситуаций с историческими задачами.

Третья часть содержит 10 вариантов диагностических работ, которые могут проверить знания по данной теме. В конце брошюры даны ответы к задачам.

 

I . Исторические и занимательные задачи

Древнеиндийская задача.

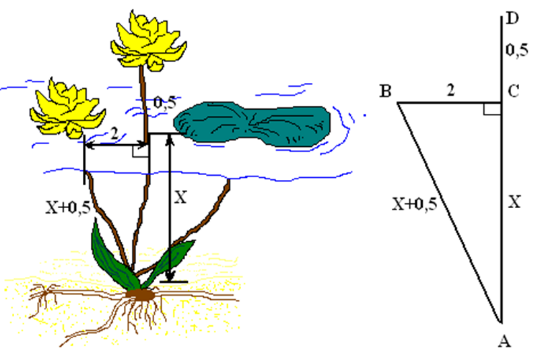Над озером тихим

С полфута размером

Высился лотоса цвет.

Он рос одиноко,

И ветер порывом

Отнес его в сторону. Нет

Боле цветка над водой.

Нашел же рыбак его

Ранней весною

В двух футах от места, где рос.

Итак, предложу я вопрос:

«Как озера вода здесь глубока?»

Решение. Пусть глубина озера 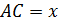, тогда  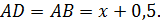Из 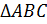 по теореме Пифагора имеем ,

,

,

.

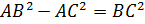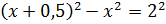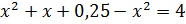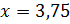Таким образом, глубина озера составляет 3,75 фута. .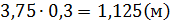

 

Ответ: 3,75 фута или 1,125 м.

 

 

3. Задача индийского математика XII в. Бхаскары.

На берегу рос тополь одинокий.

Вдруг ветра порыв его ствол надломал.

Бедный тополь упал. И угол прямой

С течением реки его ствол составлял.

Запомни теперь, что в этом месте река

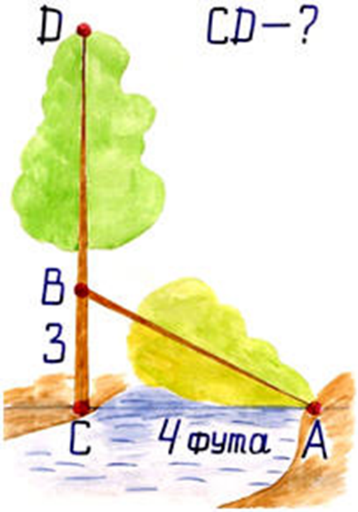В четыре лишь фута была широка

Верхушка склонилась у края реки.

Осталось три фута всего от ствола,

Прошу тебя, скоро теперь мне скажи:

У тополя как велика высота?

Решение. По теореме Пифагора

,

,

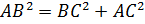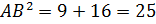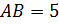 (футов) длина отломленной части ствола.

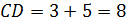 (футов) высота ствола.

 

Ответ: 8 футов.

 

Решение.

По теореме Пифагора

,

,

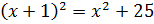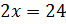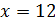 чи.;

12+1=13 чи.

 

Ответ: глубина воды – 12 чи, длина камыша – 13 чи.

 

Задача кассирши.

Три монеты лежат на столе, касаясь друг друга, а их центры образуют прямоугольный треугольник. Приведите их размеры, выраженные наименьшими возможными целыми числами.

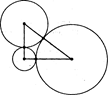Решение. Так как центры окружностей образуют прямоугольный треугольник, то для его сторон должна выполняться теорема Пифагора. Размеры должны быть наименьшими целыми числами, значит это – египетский треугольник со сторонами 3,4 и 5. Пусть радиус большей окружности равен 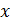, радиус средней окружности – 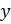, радиус меньшей окружности – 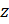. Получаем:

 

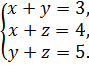
Ответ: 1, 2, 3.

 

Путь жука.

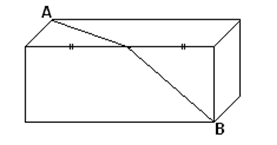У дороги лежит тесаный гранитный камень в 30см длины, 20 см высоты и такой же толщины. В точке А – жук, намеривающийся кратчайшим путем направиться к углу В. Как пролегает этот кратчайший путь и какой он длины?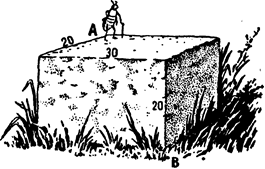

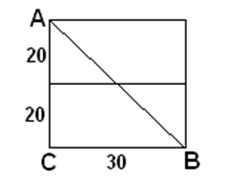Решение. Кратчайший путь легко определится, если мы мысленно повернем верхнюю грань камня так, чтобы она оказалась в одной плоскости с передней.

 Тогда АВ – кратчайший путь. АВ=50 см.

 

Ответ: 50 см.

 

 

10. 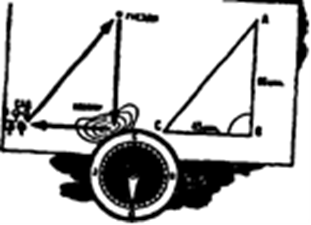Путешествие шмеля.

Шмель отправляется в дальнее путешествие. Из родного гнезда он летит прямо на юг, пересекает речку и, наконец, после целого часа пути спускается на косогор, покрытый душистым клевером. Здесь, перелетая с цветка на цветок, шмель остается полчаса. Теперь надо посетить сад, где шмель вчера заметил цветущие кусты крыжовника. Сад лежит на запад от косогора, и шмель спешит прямо туда. Спустя ¾  часа он был уже в саду. Крыжовник в полном цвету, и, чтобы посетить все кусты, понадобилось шмелю ½ часа. А затем, не отвлекаясь в стороны, шмель кратчайшей дорогой полетел домой, в родное гнездо. Сколько пробыл шмель в путешествии?

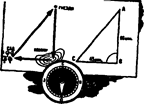Решение. Найдем, сколько времени понадобилось шмель на перелет из сада в гнездо. Начертим путь шмеля. Мы знаем, что шмель летел сначала прямо на юг в течение 60 минут. Затем он летел 45 минут на запад, то есть под прямым углом к прежнему пути. Оттуда кратчайшей дорогой, то есть по прямой линии, обратно к гнезду.

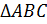 – прямоугольный.

По теореме Пифагора находим АС =75 мин = 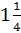 ч.

Ответ: 5 часов пробыл шмель в путешествии.

 

11.   Теорема Пифагора

Ученые собираются сложить из нанотрубок прямоугольный треугольник. Они планируют использовать 12 нанотрубок длиной 200 нм. Получится ли у них? Если да, каковы будут длины сторон прямоугольного треугольника? (Ответ обоснуйте.)

Решение. Да, получится. Например, они могут сложить треугольник со сторонами 3, 4 и 5 нанотрубок, то есть 3·200=600, 4·200=800 и 5·200=1000 нанометров.

Алгоритм решения задач по теореме Пифагора:

По условию сделай чертеж.

Найди катеты и гипотенузу.

Выполни подстановку данных.

I. Задачи из КИМов ОГЭ

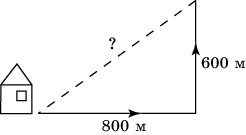
1. Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии от дома оказался мальчик?

 

 

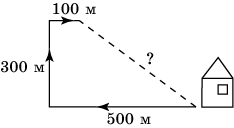
2. Девочка прошла от дома по направлению на запад 500 м. Затем повернула на север и прошла 300 м. После этого она повернула на восток и прошла еще 100 м. На каком расстоянии от дома оказалась девочка?

 

 

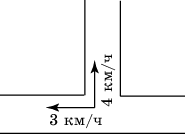
3. Мальчик и девочка, расставшись на перекрестке, пошли по взаимно перпендикулярным дорогам, мальчик со скоростью 4 км/ч, девочка 3 км/ч. Какое расстояние (в км) будет между ними через 30 мин?

 

 

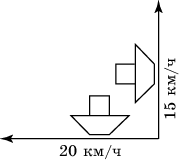
4. Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны 15 км/ч и 20 км/ч. Какое расстояние будет между ними через 2 ч?

 

 

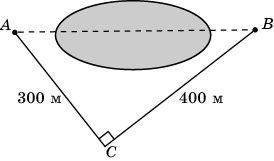
5. Используя данные, приведенные на рисунке, найдите расстояние в метрах между пунктами A и B, расположенными на разных берегах озера.

 

 

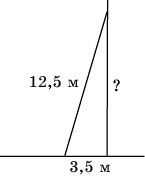
6. Лестница длиной 12,5 м приставлена к стене так, что расстояние от ее нижнего конца до стены равно 3,5 м. На какой высоте от земли находится верхний конец лестницы?

 

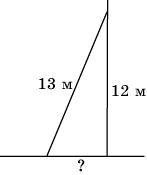
7. На какое расстояние следует отодвинуть от стены дома нижний конец лестницы, длина которой 13 м, чтобы верхний ее конец оказался на высоте 12 м?

 

 

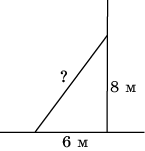
8. Какой длины должна быть лестница, чтобы она достала до окна дома на высоте 8 метров, если ее нижний конец отстоит от дома на 6 м?

 

 

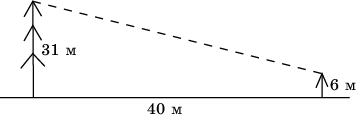
9. В 40 м одна от другой растут две сосны. Высота одной 31 м, а другой 6 м. Найдите расстояние между их верхушками.

  

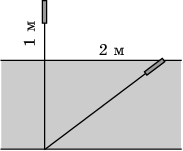
10. Стебель камыша выступает из воды озера на 1 м. Его верхний конец отклонили от вертикального положения на 2 м, и он оказался на уровне воды. Найдите глубину озера в месте, где растет камыш.

 

 

11. Из круглого бревна нужно вырезать брус с поперечным сечением 5х12 (см). Какой наименьший диаметр должно иметь бревно?

 

 

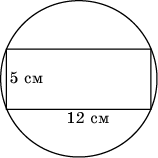
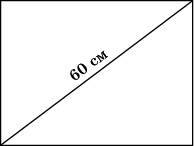
12. Отношение высоты к ширине экрана телевизора равно 0,75. Диагональ равна 60 см. Найдите ширину экрана.     

 

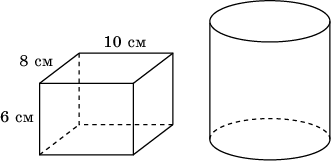
13. Какого наименьшего диаметра должен быть цилиндрический сосуд, чтобы в него можно было поместить деталь в форме прямоугольного параллелепипеда, размерами 6х8х10 (см)?

 

 

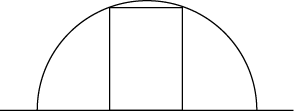
14. Туннель имеет форму полукруга радиуса 3 м. Какой наибольшей высоты должна быть машина, шириной 2 м, чтобы она могла проехать по этому туннелю? В ответе укажите приближенное значение в метрах с точностью до одного знака после запятой.

 

15. Какое наименьшее ребро должна иметь кубическая коробка, чтобы в нее поместился тетраэдр с ребром, равным 8 см? В ответе укажите целое число сантиметров.

 

 

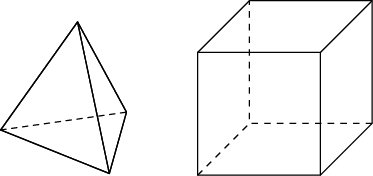
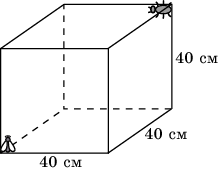
16. В одном углу кубической коробки, размерами 40х40х40 см, сидит муха. В противоположном углу сидит паук. Найдите длину кратчайшего пути по поверхности коробки, по которому паук может доползти до мухи. В ответе укажите приближенное значение, равное целому числу сантиметров.

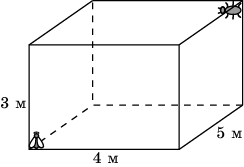
17. В одном углу комнаты, размерами 4х5х3 м, сидит муха. В противоположном углу сидит паук. Найдите длину кратчайшего пути по поверхности комнаты, по которому паук может доползти до мухи. В ответе укажите приближенное значение в метрах с точностью до одного знака после запятой.

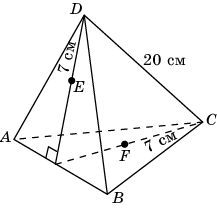
18. Найдите кратчайший путь по поверхности правильного тетраэдра ABCD, соединяющий точки E и F, расположенные на высотах боковых граней в 7 см от соответствующих вершин тетраэдра. Ребро тетраэдра равно 20 см.

           

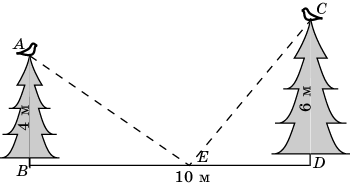
19. На вершинах двух елок сидят две вороны. Высота елок равна 4 м и 6 м. Расстояние между ними равно 10 м. На каком расстоянии BE нужно положить сыр для этих ворон, чтобы они находились в равных условиях, т.е. чтобы расстояния от них до сыра было одинаковым?

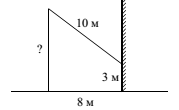
20. От стол­ба к дому на­тя­нут про­вод длиной 10м, ко­то­рый кре­пит­ся на вы­со­те 3 м от земли. Рас­сто­я­ние от дома до стол­ба 8 м. Вы­чис­ли­те высоту столба.

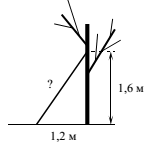
21. Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находиться на высоте 1,6 м над землей, а нижний отстоит от ствола дерев на 1,2 м?

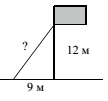
22. Точка креп­ле­ния троса, удер­жи­ва­ю­ще­го флаг­шток в вер­ти­каль­ном по­ло­же­нии, на­хо­дит­ся на вы­со­те 12 м от земли. Рас­сто­я­ние от ос­но­ва­ния флаг­што­ка до места креп­ле­ния троса на земле равно 9 м. Най­ди­те длину троса в мет­рах.

23. Определите длину линии орнамента, изображенного на рисунке.

24. Де­воч­ка про­шла от дома по на­прав­ле­нию на запад 860 м. Затем по­вер­ну­ла на север и про­шла 60 м. После этого она по­вер­ну­ла на во­сток и про­шла еще 940 м. На каком рас­сто­я­нии (в мет­рах) от дома ока­за­лась де­воч­ка?

25. Лест­ни­ца со­еди­ня­ет точки A и B . Вы­со­та каж­дой сту­пе­ни равна 10,5 см, а длина – 36 см. Рас­сто­я­ние между точ­ка­ми A и B со­став­ля­ет 15 м. Най­ди­те вы­со­ту, на ко­то­рую под­ни­ма­ет­ся лест­ни­ца (в мет­рах).

26.Лодка должна попасть на противоположный берег по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки u, а скорость лодки относительно воды v . Чему должен быть равен модуль скорости лодки относительно берега?

1) v + u

2)

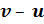
3)

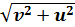
4)

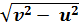
27.Тело подвешено на двух нитях и находится в равновесии. Уго между нитями равен 90°, а силы натяжения нитей равны 3 Н и 4 Н. Чему равна сила тяжести, движущая на тело?

Н

Н

Н

Н

 

28.Система состоит из двух тел 1 и 2, массы которых равна 0,5 кг и 2 кг. На рисунке стрелками в заданном масштабе 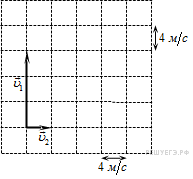указаны скорости этих тел.

1) 10 кг·м/с

2) 20кг·м/с

3) 14 кг·м/с

4) 40 кг·м/с

29. 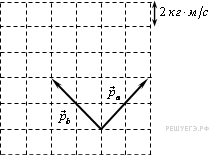Система состоит из двух тел a и b. На рисунке стрелками в заданном масштабе указаны импульсы тел. Чему по модулю равен импульс всей системы? (Ответ дайте в кг·м/с.)

 

 

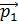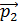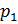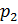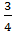30.Импульс частицы до столкновения равен  , а после столкновения равен  , причем =p , = p ,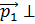  

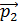
Изменение импульса частицы при 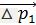 равняется по модулю

1) p

2) p

3) p

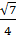4) p

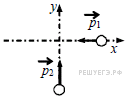
31.По гладкой горизонтальной плоскости по осям x и y движутся две шайбы с импульсами, равными 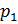=1,5 кг· м/с и 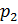=3,5 кг· м/с , как показано на рисунке. После соударения вторая шайба продолжает двигаться по оси y в прежнем направлении с импульсом, равным по модулю 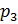=1,5 кг· м/с. Определите модуль импульса первой шайбы после удара. Ответ приведите в кг· м/с.

32.Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с.

1) 0,5 м/с

2) 0,1 м/с

3) 0,7 м/с 

33.Пловец переплывает реку по кратчайшему пути. Скорость пловца относительно воды 5 км/ч, скорость течения 3 км/ч. Чему равна скорость пловца относительно берега?

1) 2 км/с

2) 4 км/с

3) 5,8 км/с

4) 8 км/с

34.По дорогам, пересекающимся под прямым углом, едут велосипедист и автомобилист. Скорости велосипедиста и автомобилиста относительно придорожных столбов соответственно равны 8 м/с и 15 м/с. Определите модуль скорости автомобилиста относительно велосипедиста.

1) 17 м/с

2) 1 м/с

3) 3 м/с

4) 7 м/с

35.Две силы 5 н и 6 Н приложены к одному телу. Угол между направлениями сил 90°. Определите модуль равнодействующих этих сил.

 

36.Сила 6 Н и 8 Н приложены к одному телу. Угол между направлениями сил 90°. Масса тела 2 кг. Определите равнодействующую сил.

 

 

37.Пловец пересекает реку шириной 225 м. Скорость течения реки 1,2 м/с. Скорость пловца относительно воды 1,5 м/с и направленна перпендикулярно вектору скорости течения. На сколько будет снесен течением пловец к тому моменту, когда он достигнет противоположного берега?

 

38.Наблюдатель с берега видит, что пловец пересекает реку шириной 180 м перпендикулярно берегу. При этом скорость течения реки 1,2 м/с, а скорость пловца относительно воды 1,5 м/с. За какое время пловец пересечет реку?

 

39. По данным рисунка найдите длину отрезка BC.

 

 

40.Пловец переплывает реку по кратчайшему пути. Скорость пловца относительно берега 3км/ч, скорость течения 1,5км/ч. Определить скорость пловца относительно воды.

1) 2,4км/ч

2) 4,5км/ч;

3) 1,5км/ч;

4)  3,4км/ч

 

II. Диагностические работы

Вариант 1

1. Мальчик прошел от дома по направлению на восток 240 м. Затем повернул на север и прошел 320 м. на каком расстоянии (в метрах) от дома оказался мальчик?

2. В 32 м одна от другой растут две сосны. Высота одной - 37 м, а другой - 13 м. Найдите расстояние (в метрах) между их верхушками.

3. Два парохода вышли из порта, следуя один на север, а другой на запад. Скорости их равны соответственно 16 км/ч и 30 км/ч. Какое расстояние (в километрах) будет между ними через 3 ч?

4. Флагшток удерживается в вертикальном положение при помощи троса. Расстояние от основания флагштока до места крепления троса на земле равно 1,6 м. Длина троса равна 3,4 м. Найдите расстояние от земли до точки крепления троса. Ответ дайте в метрах.

5. Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?

6. Пожарную лестницу длиной 13 м приставили к окну пятого этажа дома. Нижний конец лестницы отстоит от стены на 5 м. На какой высоте расположено окно? Ответ дайте в метрах.

7. Длина стре­мян­ки в сло­жен­ном виде равна 1,85 м, а её вы­со­та в раз­ло­жен­ном виде со­став­ля­ет 1,48 м. Най­ди­те рас­сто­я­ние (в метрах) между ос­но­ва­ни­я­ми стре­мян­ки в раз­ло­жен­ном виде.

8. От стол­ба вы­со­той 9 м к дому на­тя­нут про­вод, ко­то­рый кре­пит­ся на вы­со­те 4 м от земли. Рас­сто­я­ние от дома до стол­ба 12 м. Вы­чис­ли­те длину про­во­да.

9. Лест­ни­ца со­еди­ня­ет точки A и B. Вы­со­та каж­дой сту­пе­ни равна 10,5 см, а длина равна 36 см. Рас­сто­я­ние между точ­ка­ми A и B со­став­ля­ет 7,5 м. Най­ди­те вы­со­ту, на ко­то­рую под­ни­ма­ет­ся лест­ни­ца (в мет­рах).

10. Для окраски прямоугольной стены к ней приставили лестницу длиной 6,5 м так, что верхний край лестницы приставляется к верхнему краю стены, а нижний отстоит от стены на 2,5 м. Длина этой стены равна 7 м. Найти площадь стены.

Вариант 2

1. Мальчик прошел от дома по направлению на восток 40 м. Затем повернул на север и прошел 30 м. На каком расстоянии (в метрах) от дома оказался мальчик?

2. В 21 м одна от другой растут две сосны. Высота одной - 39 м, а другой - 11 м. Найдите расстояние (в метрах) между их верхушками.

3. Два парохода вышли из порта, следуя один на север, а другой на запад. Скорости их равны соответственно 21 км/ч и 20 км/ч. Какое расстояние (в километрах) будет между ними через 2 ч?

4. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 3,6 м от земли. Расстояние от основания флагштока до места крепления тороса на земле равно 1,5 м. Найдите длину троса. Ответ дайте в метрах.

5. Лестницу длиной 2 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?

6. Лестница соединяет точки А и В и состоит из 50 ступенек. Высота каждой ступени равна 14 см, а длина – 48 см. Найдите расстояние между точками А и В (в метрах).

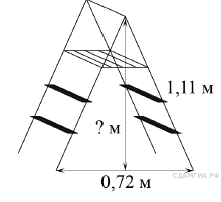
7. Длина стре­мян­ки в сло­жен­ном виде равна 1,11 м, а рас­сто­я­ние между её ос­но­ва­ни­я­ми в раз­ло­жен­ном виде со­став­ля­ет 0,72 м. Най­ди­те вы­со­ту (в мет­рах) стре­мян­ки в раз­ло­жен­ном виде.

8. По заказу мастер должен изготовить шаблон прямоугольной формы с одной диагональной перемычкой. Найдите ширину заготовки (в см), если её длинна равна 10 см, а диагональ равна 12,5 см.

9. От стол­ба вы­со­той 9 м к дому на­тя­нут про­вод, ко­то­рый кре­пит­ся на вы­со­те 3 м от земли. Рас­сто­я­ние от дома до стол­ба 8 м. Вы­чис­ли­те длину про­во­да.

10. Пожарная лестница длиной 8,5 приставили к окну третьего этажа дома. Нижний конец лестницы отстоит от стены на 1,3 м. На какой высоте расположено окно? Ответ дайте в метрах.

Вариант 3

1. Девочка прошла от дома по направлению на запад 60 м. Затем она повернула на север и прошел 700 м. После этого она повернула на восток и прошла ещё 60 м. На каком расстоянии (в метрах) от дома оказалась девочка?

2. В 24 м одна от другой растут две сосны. Высота одной - 50 м, а другой - 18 м. Найдите расстояние (в метрах) между их верхушками.

3. Два парохода вышли из порта, следуя один на север, а другой на запад. Скорости их равны соответственно 21 км/ч и 20 км/ч. Какое расстояние (в километрах) будет между ними через 5 ч?

4. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 4,8 м от земли. Расстояние от основания флагштока до места крепления тороса на земле равно 5 м. Найдите длину троса. Ответ дайте в метрах.

5. Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находиться на высоте 2,4 м над землей, а нижний отстоит от ствола дерев на 0,7 м?

6. От стол­ба вы­со­той 12 м к дому на­тя­нут про­вод, ко­то­рый кре­пит­ся на вы­со­те 4 м от земли. Рас­сто­я­ние от дома до стол­ба 15 м. Вы­чис­ли­те длину про­во­да.

7. Лестница соединяет точки А и В и состоит из 50 ступенек. Высота каждой ступени равна 28 см, а длина – 45 см. Найдите расстояние между точками А и В (в метрах).

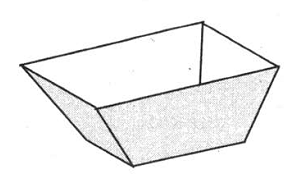
8. Имеется ящик, у которого дно – квадрат со стороной 70см, а боковины –равнобедренные трапеции, в которых большее основание равно 1,4 м, а боковая сторона равна 50 см. Внутренность этого ящика нужно покрасить краской, при чем на 1 дм² поверхности расходуется 0,002 л краски. Сколько краски потребуется для этой работы? Ответ дайте в литрах.

9. По­жар­ную лест­ни­цу дли­ной 10 м при­ста­ви­ли к окну тре­тье­го этажа дома. Ниж­ний конец лест­ни­цы от­сто­ит от стены на 6 м. На какой вы­со­те рас­по­ло­же­но окно? Ответ дайте в мет­рах.

10. Определите длину линии орнамента, изображенного на рисунке.

Вариант 4

1.  Девочка прошла от дома по направлению на запад 80 м. Затем она повернула на север и прошел 640 м. После этого она повернула на восток и прошла ещё 80 м. На каком расстоянии (в метрах) от дома оказалась девочка?

2. От стол­ба вы­со­той 12 м к дому на­тя­нут про­вод, ко­то­рый кре­пит­ся на вы­со­те 3 м от земли. Рас­сто­я­ние от дома до стол­ба 12 м. Вы­чис­ли­те длину про­во­да.

3. Два парохода вышли из порта, следуя один на север, а другой на запад. Скорости их равны соответственно 28 км/ч и 21 км/ч. Какое расстояние (в километрах) будет между ними через 5 ч?

4. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 8 м от земли. Расстояние от основания флагштока до места крепления тороса на земле равно 6 м. Найдите длину троса. Ответ дайте в метрах.

5. Лестница соединяет точки А и В и состоит из 40 ступенек. Высота каждой ступени равна 17,5 см, а длина – 60 см. Найдите расстояние между точками А и В (в метрах).

6. Глу­би­на кре­пост­но­го рва равна 8 м, ши­ри­на 5 м, а вы­со­та кре­пост­ной стены от ее ос­но­ва­ния 20 м. Длина лест­ни­цы, по ко­то­рой можно взо­брать­ся на стену, на 2 м боль­ше, чем рас­сто­я­ние от края рва до верх­ней точки стены. Най­ди­те длину лест­ни­цы.

7. Сосна высотой 7 м отбрасывает тень длиной 2,1 м. Найдите длину (в метрах) тени мальчика ростом 1,5 м, стоящего около сосны?

8. Определите длину линии орнамента, изображенного на рисунке.

9. Лест­ни­ца со­еди­ня­ет точки A и B . Вы­со­та каж­дой сту­пе­ни равна 18 см, а длина – 80 см. Рас­сто­я­ние между точ­ка­ми A и B со­став­ля­ет 41 м. Най­ди­те вы­со­ту, на ко­то­рую под­ни­ма­ет­ся лест­ни­ца (в мет­рах).

 

10.  Де­воч­ка про­шла от дома по на­прав­ле­нию на запад 700 м. Затем по­вер­ну­ла на север и про­шла 240 м. После этого она по­вер­ну­ла на во­сток и про­шла еще 520 м. На каком рас­сто­я­нии (в мет­рах) от дома ока­за­лась де­воч­ка?

Вариант 5

1.  Мальчик прошел от дома по направлению на восток 690 м. Затем повернул на север и прошел 920 м. на каком расстоянии (в метрах) от дома оказался мальчик?

2. От стол­ба к дому на­тя­нут про­вод дли­ной 13 м, ко­то­рый за­креплён на стене дома на вы­со­те 4 м от земли Вы­чис­ли­те вы­со­ту стол­ба, если рас­сто­я­ние от дома до стол­ба равно 12 м.

3. Точка креп­ле­ния троса, удер­жи­ва­ю­ще­го флаг­шток в вер­ти­каль­ном по­ло­же­нии, на­хо­дит­ся на вы­со­те 6,3 м от земли. Рас­сто­я­ние от ос­но­ва­ния флаг­што­ка до места креп­ле­ния троса на земле равно 1,6 м. Най­ди­те длину троса в мет­рах.

4. Точка креп­ле­ния троса, удер­жи­ва­ю­ще­го флаг­шток в вер­ти­каль­ном по­ло­же­нии, на­хо­дит­ся на вы­со­те 12 м от земли. Рас­сто­я­ние от ос­но­ва­ния флаг­што­ка до места креп­ле­ния троса на земле равно 5 м. Най­ди­те длину троса.

5. В 60 м одна от другой растут две сосны. Высота одной 31 м, а другой – 6 м. Найдите расстояние (в метрах) между их верхушками.

6. Имеется ящик, у которого дно – квадрат со стороной 60 см, а боковины –равнобедренные трапеции, в которых большее основание равно 1,4 м, а боковая сторона равна 50 см. Внутренность этого ящика нужно покрасить краской, при чем на 1 дм² поверхности расходуется 0,002 л краски. Сколько краски потребуется для этой работы? Ответ дайте в литрах.

7. Лестница соединяет точки А и В и состоит из 20 ступенек. Высота каждой ступени равна 25,5 см, а длина – 34 см. Найдите расстояние между точками А и В (в метрах).

8. Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находиться на высоте 2,4 м над землей, а нижний отстоит от ствола дерев на 1,8 м?

9. Два парохода вышли из порта, следуя один на север, а другой на запад. Скорости их равны соответственно 18 км/ч и 24 км/ч. Какое расстояние (в километрах) будет между ними через 5ч?

10. Определите длину линии орнамента, изображенного на рисунке.

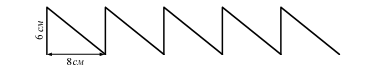
Вариант 6

1.  Какой длины должна быть лестница, чтобы она достала до окна дома на высоте 8м, если её нижний конец отстоит от дома на 6м? Ответ дайте в метрах.

 

2. Флагшток удерживается в вертикальном положении при помощи троса. Расстояние от основания флагштока до места крепления троса на земле 1,6 м. Длина троса равна 3,4 м. Найдите расстояние от земли до точки крепления троса. Ответ дайте в метрах.

3. Лест­ни­ца со­еди­ня­ет точки A и B. Вы­со­та каж­дой сту­пе­ни равна 10,5 см, а длина равна 36 см. Рас­сто­я­ние между точ­ка­ми A и B со­став­ля­ет 7,5 м. Най­ди­те вы­со­ту, на ко­то­рую под­ни­ма­ет­ся лест­ни­ца (в мет­рах).

4. Точка креп­ле­ния троса, удер­жи­ва­ю­ще­го флаг­шток в вер­ти­каль­ном по­ло­же­нии, на­хо­дит­ся на вы­со­те 4,4 м от земли. Рас­сто­я­ние от ос­но­ва­ния флаг­што­ка до места креп­ле­ния троса на земле равно 3,3 м. Най­ди­те длину троса в мет­рах.

5. По­жар­ную лест­ни­цу при­ста­ви­ли к окну, рас­по­ло­жен­но­му на вы­со­те 12 м от земли. Ниж­ний конец лест­ни­цы от­сто­ит от стены на 5 м. Ка­ко­ва длина лест­ни­цы? Ответ дайте в мет­рах.

6. Длина стре­мян­ки в сло­жен­ном виде равна 1,11 м, а рас­сто­я­ние между её ос­но­ва­ни­я­ми в раз­ло­жен­ном виде со­став­ля­ет 0,72 м. Най­ди­те вы­со­ту (в мет­рах) стре­мян­ки в раз­ло­жен­ном виде.

7. Маль­чик прошёл от дома по на­прав­ле­нию на во­сток 400 м. Затем по­вер­нул на север и прошёл 90 м. На каком рас­сто­я­нии (в мет­рах) от дома ока­зал­ся маль­чик?

8. Точка креп­ле­ния троса, удер­жи­ва­ю­ще­го флаг­шток в вер­ти­каль­ном по­ло­же­нии, на­хо­дит­ся на вы­со­те 15 м от земли. Рас­сто­я­ние от ос­но­ва­ния флаг­што­ка до места креп­ле­ния троса на земле равно 8 м. Най­ди­те длину троса.

9. Глу­би­на кре­пост­но­го рва равна 8 м, ши­ри­на 5 м, а вы­со­та кре­пост­ной стены от ее ос­но­ва­ния 20 м. Длина лест­ни­цы, по ко­то­рой можно взо­брать­ся на стену, на 2 м боль­ше, чем рас­сто­я­ние от края рва до верх­ней точки стены (см. рис.). Най­ди­те длину лест­ни­цы.

10. Де­воч­ка про­шла от дома по на­прав­ле­нию на запад 500 м. Затем по­вер­ну­ла на север и про­шла 300 м. После этого она по­вер­ну­ла на во­сток и про­шла еще 100 м. На каком рас­сто­я­нии (в мет­рах) от дома ока­за­лась де­воч­ка?

 

Вариант 7

1. От вертикального шеста ВН были натянуты под прямым углом два шнура АВ и СВ. Найдите высоту шеста (в м), если АН = 100 см, СН = 144 см.

2. Лестница состоит из 16 ступенек, шириной 25 см каждая. Найдите высоту каждой ступеньки (в см), если длина перил 5 м.

3. В парке с двух сторон от фонаря на одинаковом расстоянии (3 М) растут два дерева: ёлка высотой 1,6 м и тополь высотой 2,4 м. Найдите мину тени тополя (в метрах), если ёлка при таком освещении отбрасывает тень длиной 60 см.

4. Дерево высотой 8,8 м отбрасывает тень. Оно полностью заслоняет от солнца дерево высотой 4 м, находящееся от него на расстоянии 6 м. Определите, на какое расстояние отбрасывает тень большее дерево. Ответ дайте в метрах.

5. Между стеной и полом студии натянута верёвка. Через 4 метра от крепления на полу и в 8 метрах от стены верёвка дополнительно закреплена на штативе высотой 2,5 метра. Найдите, на какой высоте (в м) закреплена верёвка на стене.

6.  Ёлочка стоит рядом с тополем высотой 8 м. Длина тени, отбрасываемой тополем, равна 5 м, а длина тени, отбрасываемой ёлочкой, равна 1 м 40 см. Найдите высоту ёлочки (в метрах).

7. Дорожно-строительная фирма должна построить участок канатной дороги, высота которой равна 19 м, а расстояние до верхней точки равно 181 м. Вычислите длину подъёма дороги (в метрах).

8. В солнечный день человек ростом 1,6 м стоит рядом с фонарным

столбом. Длина тени человека равна 3,2 м. Длина тени, отбрасываемой фонарным столбом, равна 5,6 м. Определите высоту фонарного столба (в метрах).

9. Для того чтобы подняться на чердак, к зданию приставили лестницу длиной 3,7 метра, так, что расстояние её нижнего конца до здания равно 1,2 метра. Найдите, на какой высоте от земли находится верхний конец лестницы.

10.  Прожектор освещает фасад здания высотой 4,5 м, расположенный на расстоянии 7,5 м от прожектора. На каком наименьшем расстоянии (в метрах) от прожектора нужно расположить рекламный щит высотой 3 м, чтобы он был полностью освещён, если настройки прожектора оставить без изменения?

Вариант 8

1.  На расстоянии 16 шагов от столба был вбит кол высотой 2,3 м. Определите высоту фонарного столба (в метрах), если длина тени кола 8 шагов.

2. Найдите расстояние (в м) между двумя прожекторами, закреплёнными на штативах, если эти прожекторы закреплены на высоте 2 м и 8 м, и расстояние между штативами 8 метров.

3. Длина тени от дома равна 12 м, а длина тени мальчика ростом 1,5 м

составляет 1,2 м. Определите высоту дома. Ответ дайте в метрах.

4. Дерево высотой 7 м отбрасывает тень. Оно полностью заслоняет от солнца ель высотой 2 м, находящуюся на расстоянии 7 м от большего дерева. Определите, на какое расстояние ель отбрасывает тень. Ответ дайте в метрах.

5. Удочка закреплена на берегу с помощью двух креплений А и В. Крепление В находится на расстоянии 40 см от одного конца удочки и 1,2 м от другого. На сколько сантиметров поднимется длинный конец удочки, если короткий опустить на 5 См? (Считается, что крепление В неподвижно.)

6. Расстояние по прямой линии от Испериха в Тутракан и Дулово равно 40 км и 28 км соответственно. Соединяя три города, получаем прямой угол в Исперихе. Найдите расстояние от Дулово до Тутракана.

7. Стороны прямоугольника равны 10 см и 24 см. Найти радиус окружности, описанной вокруг прямоугольника.

8. Гипотенуза прямоугольного треугольника равна 10 cм, а одна из его сторон - 8 cм. Найдите периметр треугольника.

9. В параллелограмме ABCD АВ = 33см, BC = 56 см и АС = 65 см. Проверьте, является ли этот параллелограмм прямоугольником.

10. Мальчику Вите требуется измерить ширину пруда. Он нашёл расстояния от пункта R до пунктов P и Q, расположенных по разным сторонам пруда, как показано на рисунке ниже, и уверился в том, что угол P – прямой. Если допустить, что расчёты верны, какова протяжённость пруда с запада на восток?

Дано: расстояние от точки R до точки P (катет треугольника) равняется 24, от точки R до точки Q (гипотенуза) – 26.

 

Вариант 9

1. Для крепления мачты нужно установить четыре троса. Один конец каждого троса должен крепиться на высоте 12 м, другой – на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?

2. Разгадайте ребус. В ребусе содержится важная характеристика фигуры в теореме Пифагора.

 

 

3. Кролик пробежал от норы по направлению на восток 40 м. Затем повернул на север и пробежал 30 м. На каком расстоянии (в метрах) от норы оказался кролик?

4. Пловец поплыл от берега реки, всё время, гребя в направлении по перпендикуляру к берегу (берега реки считаем параллельными). Плыл он, приближаясь к противоположному берегу со скоростью 3 км/ч. Через 5 минут он был на противоположном берегу реки. На каком расстоянии от места начала заплыва он вышел на противоположном берегу, считая скорость течения всюду равной 6 км/ч?

5. Найдите периметр прямоугольника EFKT. Где KT=8 см, а диагональ этого прямоугольника, KE=17см.

6. Найдите высоту прямоугольного треугольника, проведённую из вершины прямого угла, если гипотенуза равна 8, а один из острых углов равен 60°.

7. Найдите расстояние от центра окружности радиуса 10 до хорды длиной 12.

8. Точка M находится на расстоянии 26 от центра окружности радиуса 10. Прямая MA касается окружности в точке A. Найдите длину отрезка MA.

9. Один из катетов прямоугольного треугольника равен 15, а проекция второго катета на гипотенузу равна 16. Найдите гипотенузу и второй катет.

10. Одно основание прямоугольной трапеции вдвое больше другого, а боковые стороны равны 4 и 5. Найдите диагонали трапеции.

Вариант 10

1. Разгадайте ребус. В этом ребусе зашифровано имя математика, которому приписывают открытие важнейших теорем геометрии.

 

 

2. Лестницу длиной 5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 3 м?

3. В равнобокой трапеции высота равна 6см, диагональ равна 10см, большее основание равно 11см. Найдите другое основание.

4. В окружности радиуса 13 см проведена хорда на расстоянии 5 см от центра окружности. Найдите длину хорды.

5. В 24 м одна от другой растут две сосны. Высота одной - 50 м, а другой - 18 м. Найдите расстояние (в метрах) между их верхушками.

6. В прямоугольник ABCD смежные стороны относятся как 12:5, а его диагональ равна 26 см. Чему равна меньшая сторона прямоугольника?

7. Диагонали ромба равны 24 см и 18 см. Чему равна сторона ромба?

8. Две окружности радиусов 13 см и 15 см пересекаются. Расстояние между их центрами О₁ и О₂ равно 14 см. Общая хорда этих окружностей АВ пересекает отрезок О₁О₂ в точке К. Найдите О₁К и КО₂ (О₁ – центр окружности радиуса 13 см).

9. Продолжения боковых сторон трапеции пересекаются под прямым углом. Большая боковая сторона равна 8, а разность оснований равна 10. Найдите меньшую боковую сторону.

10. Для крепления мачты нужно установить четыре троса. Один конец каждого троса должен крепиться на высоте 12 м, другой – на земле на расстоянии 5 м от мачты. Хватит ли 52 м троса для крепления мачты?

 

Заповеди Пифагора

· Не делай ничего постыдного ни в присутствии других, ни втайне. Первым твоим законом должно быть уважение к себе самому.

· Не закрывай глаз, когда хочешь спать, не разобравши всех своих поступков за прошедший день.

· Будь другом истины до мученичества, но не будь ее защитником до нетерпимости.

· Полезнее наобум бросить камень, чем пустое слово.

· Прежде всего не теряй самоуважения!

· Все исследуй, давай разуму первое место.

· Делай великое, не обещая великого.

· Для познания нравов какого ни есть народа старайся прежде изучить его язык.

· Если можешь быть орлом, не стремись стать первым среди галок.

· Жизнь подобна игрищам: иные приходят на них состязаться, иные — торговать, а самые счастливые — смотреть.

· Избери себе друга; ты не можешь быть счастлив один: счастье есть дело двоих.

· Как ни коротки слова «да» и «нет», все же они требуют самого серьезного размышления.

· Молчи или говори что-нибудь получше молчания.

· Делай лишь то, что впоследствии не огорчит тебя и не принудит раскаиваться.

· Помогай не тому, кто ношу сваливает, а тому, кто её взваливает.

 

 

Ответы

1. 1000 2. 500 3. 2,5 4. 50 5. 500 6. 12 7. 5  8. 10  9. 65 10. 1,5 11. 13 12. 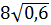13. 10 14. 2,8 15. 5 16. 96,6 17. 10 18. 20,6 19. 6 20. 9 21. 2 22. 15 23. 72 24. 100 25. 4,2  26. 4 27. 2 28. 1 29. 8 30. 8 31. 2,5 32. 0,7 33. 2 34. 1 35. 5 36. 5 37. 193 38. 200 39. 12 40. 4  

Ответы к диагностическим работам

№                     задания Вариант	1	2	3	4	5	6	7	8	9	10
1	400	40	102	3	3,4	12	10	13	2,1	42
2	50	35	58	3,9	1,6	7	1,05	7,5	10	8,4
3	700	40	145	1,4	2,5	17	26,5	0,418	8	36
4	640	15	175	10	25	15	2,1	55	9	300
5	1150	9	6,5	10	65	0,312	8,5	3	150	80
6	10	3	2,1	5,5	13	1,05	410	17	15	500
7	1,2	18,72	1	11	75	2,4	180	2,8	3,5	5
8	6,9	10	1,5	2,8	15	50	13	24	да	10
9	нет	Прямой угол	50	250	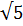46	2	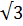8	24	25 и 20	5 и 2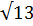
10

Список литературы

1. Г.И. Глейзер, «История математики в школе», Москва , «Просвещение» ,1982г.

2. Г.П.Бевз, И.Г.Владимирова ,«Геометрия 7-11класс»,1994г.

3. А.Д.Александров, «Геометрия 8-9», Москва, «Просвещение», 1991г.

4. Л.И.Звавич, А.Р.Рязановский «Геометрия в таблицах 7-11 классы» Москва. Издательский дом «Дрофа» ,1997г.

5. Б.Г.Зив, В.Н.Мейлер ,«Задачи по геометрии», Москва «Просвещение», 2000г

6. А.Л. Семенова и И.В. Ященко «ЕГЭ. Универсальные материалы для подготовки учащихся», Ярославль «Интеллект-центр», 2015

7. И.Р. Высоцкий «Самое полное издание типовых вариантов заданий ЕГЭ» Москва «Астрель», 2015

8. Акимова С. Занимательная математика, серия «Нескучный учебник». – Санкт-Петербург: Тригон, 1997.

9. Волошников А.В. Пифагор: союз истины, добра и красоты. – М.: Просвещение, 1993.

10. Я познаю мир: Детская энциклопедия: Математика. – М.: Аванта+, 1997.

11. Еленьский Ш. По следам Пифагора. - М, 1961.

12. Литцман В. Теорема Пифагора. - М.: Просвещение, 1960.

13. Скопец З.А. Геометрические миниатюры. - М .: Просвещение, 1990.

14. Энциклопедический словарь юного математика / Сост. А.П. Савин. – 3-е изд., испр. и доп. - М.: Педагогика–Пресс, 1997, с. 271.

15. Энциклопедия для детей. Т.11. Математика / Глав. ред. М.Д. Аксёнова. - М.: Аванта+, 1998.

Электронные источники:

• Рефераты и сочинения в помощь школьнику. Дискавери – 2015. http://www.referat-sochinenie.ru/

• Большая энциклопедия Кирилла и Мефодия. – 2015. http://dic.academic.ru/

• Электронная энциклопедия: Star World

• Сдам ГИА http://sdamgia.ru/

• «Федеральный институт педагогических измерений» http://www.fipi.ru/

 

Содержание

Введение ……………………………………………………………………………… 3

I. Исторические и занимательные задачи ………………………………….. 4

II. Задачи из КИМов ОГЭ…………………………………………………….. 9

III. Диагностические работы ………………………………………………… 20

Заповеди Пифагора………………………………………………………………….. 29

Ответы ……………………………………………………………………………….. 30

Список литературы …………………………………………………………………. 31

ТЕОРЕМА ПИФАГОРА

 В ЗАДАЧАХ РЕАЛЬНОЙ МАТЕМАТИКИ

 (сборник задач с практическим содержанием,

решаемых с помощью теоремы Пифагора)

 

Составители:

П. Е. Алдохина	- обучающаяся 10 А класса МБОУ «Золотухинская средняя общеобразовательная школа»
Е. А. Гоменюк	- обучающаяся 10 А класса МБОУ «Золотухинская средняя общеобразовательная школа»
Л. М. Семенихина	- учитель математики МБОУ «Золотухинская средняя общеобразовательная школа»

 

 

Алдохина П. Е., Гоменюк Е. А., Семенихина Л. М.

Теорема Пифагора в задачах реальной математики. Сборник задач с практическим содержанием, решаемых с помощью теоремы Пифагора, 2017г. – 30с.

Брошюра может быть использована в качестве дополнительного сборника задач при изучении геометрии в 8 -11-х классах, при организации обобщающего повторения в

9 – 11-х классах, в работе кружков, курсов по выбору или элективных курсов по математике, а также при подготовке к ОГЭ и ЕГЭ по математике.

 

 

ВВЕДЕНИЕ

    Теорема Пифагора по праву является одной из основных теорем математики. Значение этой теоремы заключается в том, что при ее помощи можно вывести большую часть теорем геометрии. Ценность ее в современном мире также велика, поскольку теорема Пифагора применяется во многих отраслях деятельности человека. Например, ее используют при расположении молниеотводов на крышах зданий, при производстве окон некоторых архитектурных стилей и даже при вычислении высоты антенн операторов мобильной связи. И это далеко не весь перечень практического применения данной теоремы. Вот почему очень важно знать теорему Пифагора и понимать ее практическое значение. С этой целью практические задачи, которые решаются с помощью теоремы Пифагора, включены в КИМы ОГЭ и ЕГЭ по математике.

    Данная брошюра содержит задачи с практическим содержанием, решаемые с помощью теоремы Пифагора, причем демонстрируется ее применение при решении задач в различных областях человеческой деятельности.

Книга разделена на 3 части.

Первая часть содержит исторические и занимательные задачи с решениями, найденные в различных источниках.

Во второй части собраны задачи из КИМов ОГЭ по математике. Предлагаемые задачи сопровождаются рисунками, позволяющими лучше понять условие, представить соответствующую геометрическую ситуацию, наметить план решения, при необходимости провести дополнительные построения и вычисления, а главное, увидеть связь современных реальных ситуаций с историческими задачами.

Третья часть содержит 10 вариантов диагностических работ, которые могут проверить знания по данной теме. В конце брошюры даны ответы к задачам.

 

I . Исторические и занимательные задачи