Відповідно до критерію II результати спостережень Ii належать нормальному закону розподілу, якщо не більш за m різниць 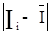 перевершили значення
перевершили значення 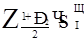 ,
,
де 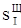 - незміщена оцінка СКВ результатів спостережень Ii, а
- незміщена оцінка СКВ результатів спостережень Ii, а 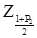 - верхня квантиль розподілу інтегральної функції нормованого нормального розподілу, відповідна довірчій вірогідності Р2.
- верхня квантиль розподілу інтегральної функції нормованого нормального розподілу, відповідна довірчій вірогідності Р2.
Незміщену оцінку СКВ результатів спостережень Сi розрахуємо по формулі:
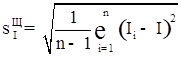 ; (4.6)
; (4.6)
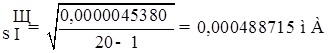 .
.
Значення m і Р2 знаходимо по числу спостережень n і рівню значущості α2 для критерію II. Потім обчислимо:
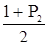 =
=  . (4.7)
. (4.7)
Для n=20 і α2=0,05, маємо m=1 і Р2=0,98, отже:
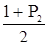 =
= 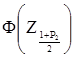 =
= 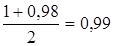 .
.
Знаходимо 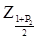 , відповідне обчисленому значенню функції:
, відповідне обчисленому значенню функції:
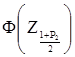 .
.
Для 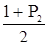 =
= 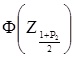 =0,99 виконаємо квадратичну інтерполяцію. Використовуючи таблицю 4.5, знайдемо
=0,99 виконаємо квадратичну інтерполяцію. Використовуючи таблицю 4.5, знайдемо 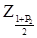 за допомогою наступної формули:
за допомогою наступної формули:
Z=Z1+ 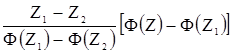 , (4.8)
, (4.8)
де Z - шукане значення 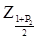 для функції
для функції 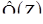 =
= 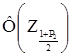 =0,99;
=0,99;
Z1 - значення 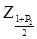 відповідне функції
відповідне функції 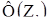 =
= 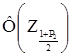 =0,9895;
=0,9895;
Z2 - значення 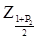 відповідне функції
відповідне функції 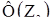 =
= 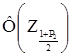 =0,9901.
=0,9901.
Z=2,57+ 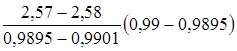 =2,578.
=2,578.
Отже, 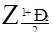 =2,578.
=2,578.
Таблиця 4.5 Значення функції 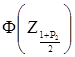
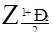
| 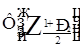
|
| 2,57 | 0,9895 |
| Z | 0,9900 |
| 2,58 | 0,9901 |
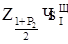 =
=  ·2,578=1,26∙10-3 мА.
·2,578=1,26∙10-3 мА.
Значення 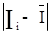 жодного разу не перевершили значення
жодного разу не перевершили значення 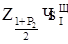 =1,26∙10- 3 мА, отже, розподіл результатів спостережень задовольняє і критерію II.
=1,26∙10- 3 мА, отже, розподіл результатів спостережень задовольняє і критерію II.
В результаті проведених розрахунків можна зробити висновок, що експериментальний закон розподілу відповідає нормальному закону.
Оцінка анормальності окремих результатів спостережень
Проведемо перевірку грубих похибок результатів спостережень або, по-іншому, оцінку анормальності окремих результатів спостережень. Для цього:
а) складемо впорядкований ряд результатів спостережень (таблиця 4.6), розташуємо початкові елементи в порядку зростання і виконаємо їх перенумерацію;
б) для крайніх членів (результатів спостережень) впорядкованого ряду I1 і I20, які найбільш віддалені від центру розподілу (визначуваного як середнє арифметичне 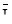 цього ряду) і тому з найбільшою вірогідністю можуть містити грубі похибки, знайдемо модулі різниць
цього ряду) і тому з найбільшою вірогідністю можуть містити грубі похибки, знайдемо модулі різниць 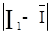 ,
, 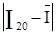 , і для більшого обчислимо параметр t, який визначається співвідношенням:
, і для більшого обчислимо параметр t, який визначається співвідношенням:
t= 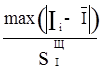 , (4.9)
, (4.9)
де 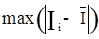 - найбільше значення
- найбільше значення 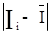 при
при 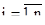 :
:
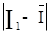 =
= 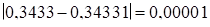 мА;
мА;
Таблиця 4.6 Початкові елементи в порядку їх зростання
| Номер експерименту, i | Результат експерименту, Ii, мА |
| 1 | 0,3433 |
| 2 | 0,3436 |
| 3 | 0,3426 |
| 4 | 0,3425 |
| 5 | 0,3425 |
| 6 | 0,3441 |
| 7 | 0,3436 |
| 8 | 0,3442 |
| 9 | 0,3435 |
| 10 | 0,3432 |
| 11 | 0,3434 |
| 12 | 0,3432 |
| 13 | 0,3434 |
| 14 | 0,3432 |
| 15 | 0,3428 |
| 16 | 0,3439 |
| 17 | 0,3430 |
| 18 | 0,3434 |
| 19 | 0,3430 |
| 20 | 0,3438 |
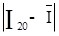 =
= 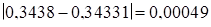 мА;
мА;
t= 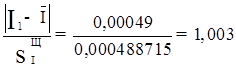 ;
;
в) за допомогою значень параметра tТ, входом якої є число елементів вибірки n і задана довірча ймовірність Р (або рівень значущості α), знайдемо теоретичне або граничне значення параметра tТ і порівняємо його з обчисленим фактичним значенням параметра t.
Отже, для n=20, Р=0,95 (α=1-Р=1-0,95=0,05) маємо tТ=2,623.
Критерієм анормальності результату спостережень Ii є умова t 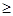 tТ. Оскільки 1,003<2,623, то елемент вибірки не виключається з розгляду.
tТ. Оскільки 1,003<2,623, то елемент вибірки не виключається з розгляду.
Дата: 2019-05-29, просмотров: 311.