Практична користь будь-якого вимірювання визначається вказанням його похибки, тобто кількісної характеристики відхилення результату вимірювання від істинного значення вимірюваної фізичної величини.
Під час виготовлення світильників необхідно дотримуватися багатьох норм та параметрів, які пред’являються готовій продукції. В таблиці 4.1 наведені результати вимірювання струму витоку під час підключення до контактних затискачів світильників дротів з найбільш допустимим січенням. Відомо, що результати експерименту Іі, 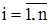 , де n=20 – кількість результатів, виміряних з довірчою ймовірністю Р=0,95.
, де n=20 – кількість результатів, виміряних з довірчою ймовірністю Р=0,95.
Таблиця 4.1 – Результати виміру електричного струму
| Номер експерименту, і | Результат експерименту, Ii, мА |
| 1 | 0,3433 |
| 2 | 0,3436 |
| 3 | 0,3426 |
| 4 | 0,3425 |
| 5 | 0,3425 |
| 6 | 0,3441 |
| 7 | 0,3436 |
| 8 | 0,3442 |
| 9 | 0,3435 |
| 10 | 0,3432 |
| 11 | 0,3434 |
| 12 | 0,3432 |
| 13 | 0,3434 |
| 14 | 0,3432 |
| 15 | 0,3428 |
| 16 | 0,3439 |
| 17 | 0,3430 |
| 18 | 0,3434 |
| 19 | 0,3430 |
| 20 | 0,3438 |
Проаналізуємо серію результатів спостережень на наявність промахів. Промахами або аномальними результатами вимірювання називаються результати вимірювання з надмірними похибками і, якщо вони є, їх обов’язково виключають з подальшої обробки. В нашому випадку промахи відсутні.
Перевіримо відповідність експериментального закону розподілу результатів спостережень Іі нормальному. Для цього використовують різні критерії згоди, серед яких найбільш широке застосування знаходить складений критерій.
Складений критерій включає два незалежні критерії, їх позначають І і ІІ. Перший з цих критеріїв (критерій I) забезпечує перевірку відповідності розподілу експериментальних даних нормальному закону поблизу центру розподілу, а другий критерій (критерій II) - на краях розподілу. Якщо при перевірці не задовольняється хоча б один з цих критеріїв, то гіпотеза про нормальність розподілу результатів спостережень відкидається.
4.2 Перевірка гіпотези про нормальність по критерію І
Для перевірки гіпотези про нормальність розподілу початкової серії результатів спостережень по критерію I обчислюють параметр d, який визначається співвідношенням:
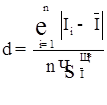 , (4.1)
, (4.1)
де 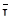 - середнє арифметичне результатів спостережень Iі,
- середнє арифметичне результатів спостережень Iі, 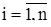 ;
;
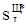 - зміщена оцінка середньоквадратичного відхилення (СКВ) результатів спостережень Iі.
- зміщена оцінка середньоквадратичного відхилення (СКВ) результатів спостережень Iі.
Середнє арифметичне результатів спостережень розрахуємо по співвідношенню:
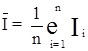 . (4.2)
. (4.2)
Отримуємо 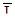 =0,34331 мА.
=0,34331 мА.
Значення зміщеної оцінки СКВ результатів спостережень знаходиться по формулі:
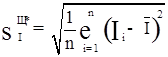 . (4.3)
. (4.3)
Для полегшення подальших розрахунків зведемо 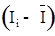 і
і 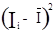 в таблицю 4.2.
в таблицю 4.2.
Таблиця 4.2 – Розрахунки по складеному критерію
| і | 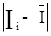 , мА , мА
| 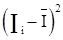 , мА2 , мА2
|
| 1 | -0,00001 | 0,0000000001 |
| 2 | 0,00029 | 0,0000000841 |
| 3 | -0,00071 | 0,0000005041 |
| 4 | -0,00081 | 0,0000006561 |
| 5 | -0,00081 | 0,0000006561 |
| 6 | 0,00079 | 0,0000006241 |
| 7 | 0,00029 | 0,0000000841 |
| 8 | 0,00089 | 0,0000007921 |
| 9 | 0,00019 | 0,0000000361 |
| 10 | -0,00011 | 0,0000000121 |
| 11 | 0,00009 | 0,0000000081 |
| 12 | -0,00011 | 0,0000000121 |
| 13 | 0,00009 | 0,0000000081 |
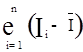 =0.
=0.
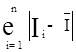 =0,0076 мА.
=0,0076 мА.
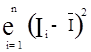 =0,0000045380 мА2.
=0,0000045380 мА2.
Розрахуємо зміщену оцінку СКВ 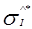 відповідно до співвідношення (4.3):
відповідно до співвідношення (4.3):
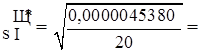 0,00047634 мА.
0,00047634 мА.
Розрахуємо параметр d відповідно до співвідношення (4.1):
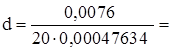 0,797749.
0,797749.
Результати спостережень Ii вважаються за результати, розподілені по нормальному закону, якщо виконується умова
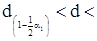
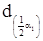 , (4.4)
, (4.4)
де 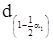 ,
, 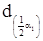 - квантилі розподілу параметра d значень α - процентних точок розподілу параметра d, за заданим обсягом вибірки n і прийнятому для критерію I рівню значущості α1.
- квантилі розподілу параметра d значень α - процентних точок розподілу параметра d, за заданим обсягом вибірки n і прийнятому для критерію I рівню значущості α1.
Приймемо α1 і α2 так, щоб виконалася умова α≤α1+α2, де α=1-Р=
=1-0,95=0,05. Візьмемо α1=0,02 і α2=0,05.
При n=20 і α1=0,02 виконаємо квадратичну інтерполяцію (необхідні для цього значення параметра 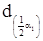 наведені в таблиці 4.3), знайдемо
наведені в таблиці 4.3), знайдемо 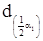 за допомогою наступної формули:
за допомогою наступної формули:
Y=Y1+ 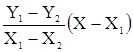 , (4.5)
, (4.5)
де Y - шукане значення параметра 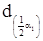 для X=n=20;
для X=n=20;
Y1 - значення параметра 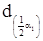 відповідне X1=n1=16;
відповідне X1=n1=16;
Y2 - значення параметра 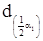 відповідне X2=n2=21.
відповідне X2=n2=21.
Таблиця 4.3 Значення параметру 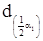
| n | 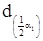
|
| 16 | 0,9137 |
| 20 | Y |
| 21 | 0,9001 |
Y= 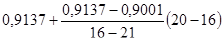 =0,9028.
=0,9028.
Отже, 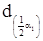 =0,9028.
=0,9028.
Для знаходження 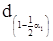 виконаємо таку ж інтерполяцію, використовуючи співвідношення (4.5) й таблицю 4.4:
виконаємо таку ж інтерполяцію, використовуючи співвідношення (4.5) й таблицю 4.4:
Y= 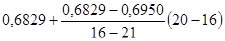 =0,6956.
=0,6956.
Таблиця 4.4 Значення 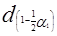
| n | 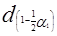
|
| 16 | 0,6829 |
| 20 | Y |
| 21 | 0,6950 |
Отже, 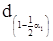 =0,6956.
=0,6956.
Перевіримо виконання умови (4.4):
0,6956<0,797749<0,9028.
Оскільки воно виконується, перевірка проводиться згідно з критерієм II.
Дата: 2019-05-29, просмотров: 342.