Основу расчётов в инвестиционном анализе составляют более сложные методы, основанные на использовании математических приёмов, а именно методы:

ü дисконтирования;

ü компаундинга;

ü расчёта внутренней нормы доходности.

Каждый из перечисленных методов учитывает влияние на финансовые результаты фактора времени, принятых ставок банковских ссуд, депозитов, инфляции, риска.

Действительно, манат, доллар, франк, единица любой другой денежной валюты, полученная через год или через 10 лет, стоит меньше, чем тот же манат, доллар, франк, получаемые сегодня. Поэтому для оценки текущей стоимости будущих поступлений и, наоборот, для оценки будущей стоимости имеющихся сегодня средств необходимо сделать соответствующие поправки вышеуказанными методами компаундинга и дисконтирования. Рассмотрим механизм использования этих методов.

Итак, компаундинг – это расширение, накопление через сложный процент. Суть метода компаундинга состоит в том, что мы можем подсчитать, как вырастет базовая сумма капитала при ежегодном проценте прироста дохода. Эту технику набегающего сложного процента иногда сравнивают со снежным комом. При начислении сложного процента мы находим будущую стоимость путём умножения текущей стоимости на множитель (1 + ставка процента) столько раз, на сколько лет мы делаем расчёт:

FV = PV (1 + r ) ⁿ                                                                                 

где FV - будущая стоимость денежного потока капитала;

   PV – текущая его стоимость;

    r - ставка дохода (отношение чистого дохода к вложенному капиталу);

    n - число лет.

Например, 1 000 ман., вложенных в бизнес под 10% роста, при условии ежегодного реинвестирования дохода через 5 лет возрастет до 1 610,5 ман.

(1 000´(1+0,1)⁵).

Дисконтирование – обратный процесс, это приведение будущих доходов к сегодняшнему моменту времени, т.е. расчёт настоящей, текущей стоимости будущего потока капитала:

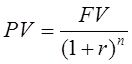
Чистая стоимость каждого года (PV) – это то, насколько ценится соответствующий будущий доход (FV) сегодня, поскольку решения об инвестировании, его перспективности надо принимать сейчас.

Чистая приведённая стоимость (NPV) проекта представляет собой разность между суммарной текущей стоимостью будущих денежных потоков за каждый год и суммой первоначальных инвестиционных затрат. Говоря другими словами, процесс вычисления чистой приведённой величины дохода выглядит следующим образом:

1. вычислить текущие стоимости всех ежегодных денежных потоков;

2. сложить все дисконтированные денежные потоки;

3. вычесть инвестиционный расход из общей суммы дисконтированных денежных потоков.

     NPV используется для оценивания различных предложений об инвестициях с использованием общей базы для сравнения. Причём при альтернативных вариантах инвестирования надо выбирать вариант с максимальной положительной разностью между суммой приведённых стоимостей и первоначальным вложением. Чем выше текущая приведённая стоимость будущих доходов, тем предпочтительнее данное вложение капиталов, так как именно чистая приведённая стоимость показывает рост благосостояния владельцев компании, которая достижима при принятии проекта. Наоборот, отрицательная величина NPV указывает на то, что доходы от предложенной инвестиции недостаточно высоки, чтобы компенсировать риск, присущий данному проекту, поэтому данное предложение должно быть отклонено.

Показатель чистой приведённой стоимости (NPV) обычно считается самым надёжным показателем бюджета инвестиции, но он не может быть единственным средством оценки спрогнозированных денежных потоков. Поскольку VPV определяет величину отдачи от инвестиции, то, скорее всего, чем больше инвестиция, тем больше будет результат. Следовательно, результаты сравнения разных по объёму инвестиций будут искажены, если для их оценки использовать только NPV.

 Поэтому всегда целесообразно дополнительно рассчитывать показатель внутренней нормы доходности (или прибыли) предлагаемого проекта.

 Внутренняя норма прибыли (IRR) – это та процентная ставка дисконтирования, при которой чистая приведённая стоимость (NPV) или эффект от инвестиций равен нулю. Говоря иначе, это та расчётная ставка процентов, при которой приведённая стоимость будущих денежных потоков равняется первоначальной сумме инвестиций, следовательно, капиталовложения окупаются. Значение IRR, при котором проект можно считать привлекательным, должно превышать условную стоимость капитала инвестора, например ставку по долгосрочным банковским кредитам, в противном случае - проект невыгоден. Этот показатель используется также как и показатель чистой приведённой стоимости для оценки эффективности инвестирования, только сравнение идёт по результату от проекта – получим или нет прибыль и на сколько максимально к границе внутренней нормы прибыли (желательно, чтобы выбранная процентная ставка дисконтирования была как можно дальше до этой границы).         

Расчёт IRR представляет определённую сложность. Его точное значение определяется исходя из выполнения равенства:  

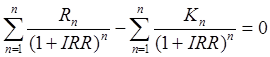
где R_n - будущие денежные потоки соответствующего года; 

  K_n - первоначальные инвестиционные затраты.

Однако возможен приближённый расчёт внутренней нормы доходности с помощью итеративного процесса. Он начинается с приближённого задания барьерной ставки, при которой нужно будет дисконтировать будущие денежные поступления и такой, чтобы их суммарная текущая стоимость равнялась текущей стоимости начальных расходов - инвестиций. Затем полученное значение чистой приведённой величины дохода сравнивается с нулём. Если она положительна, то в следующий раз будет использована более высокая ставка. Если она отрицательна, то будет пробоваться более низкая ставка. Рамки для ставки дисконтирования постепенно сужаются, пока не наступит «касание» и не найдётся та ставка дисконтирования, при которой чистая приведённая стоимость проекта будет равна нулю.