При планировании и подведении результатов эксперимента существенную роль играют статистические методы, которые дают, в том числе, возможность устанавливать степень достоверности сходства и различия исследуемых объектов на основании результатов измерений их показателей. Следовательно, при проведении педагогического эксперимента необходимо обосновать, что состояние объекта изменилось, причем в требуемую сторону. Но этого оказывается недостаточно. Нужно обосновать, что изменения произошли именно в результате произведенного воздействия.
Для того, чтобы выделить в явном виде результат целенаправленного воздействия на исследуемый объект, необходимо взять аналогичный объект и посмотреть, что происходит с ним в отсутствии воздействий. Традиционно эти два объекта в экспериментальных исследованиях называют соответственно экспериментальной группой (например, обучаемой по предложенной методике) и контрольной группой (например, обучаемой по традиционной методике).
Типовой задачей анализа данных в педагогических исследованиях является установление совпадений или различий характеристик экспериментальной и контрольной группы. Для этого формулируются статистические гипотезы:
- гипотеза об отсутствии различий (так называемая нулевая гипотеза);
- гипотеза о значимости различий (так называемая альтернативная гипотеза).
Для принятия решений о том, какую из гипотез (нулевую или альтернативную) следует принять, используют решающие правила – статистические критерии. То есть, на основании информации о результатах наблюдений (характеристиках членов экспериментальной и контрольной группы) вычисляется число, называемое эмпирическим значением критерия. Это число сравнивается с известным (например, заданным таблично) эталонным числом, называемым критическим значением критерия.
Критические значения приводятся, как правило, для нескольких уровней значимости. Уровнем значимости называется вероятность ошибки, заключающейся в отклонении (не принятии) нулевой гипотезы, то есть вероятность того, что различия сочтены существенными, а они на самом деле случайны. Обычно используют уровни значимости (обозначаемые a), равные 0,05, 0,01 и 0,001. В педагогических исследованиях обычно ограничиваются значением 0,05, то есть, грубо говоря, допускается не более чем 5% возможность ошибки. Если полученное исследователем эмпирическое значение критерия оказывается меньше или равно критическому, то принимается нулевая гипотеза – считается, что на заданном уровне значимости (то есть при том значении a, для которого рассчитано критическое значение критерия) характеристики экспериментальной и контрольной групп совпадают. В противном случае, если эмпирическое значение критерия оказывается строго больше критического, то нулевая гипотеза отвергается и принимается альтернативная гипотеза – характеристики экспериментальной и контрольной группы считаются различными с достоверностью различий 1 – a. Например, если a = 0,05 и принята альтернативная гипотеза, то достоверность различий равна 0,95 или 95%. Другими словами, чем меньше эмпирическое значение критерия (чем левее оно находится от критического значения), тем больше степень совпадения характеристик сравниваемых объектов. И наоборот, чем больше эмпирическое значение критерия (чем правее оно находится от критического значения), тем сильнее различаются характеристики сравниваемых объектов.
Е.В.Сидоренко и О.Ю.Ермолаев предложили следующую классификацию задач и методов их решения.
Таблица 1- Соответствие задач и методов решения
| Задачи | Условия | Методы |
| 1. Выявление различий в уровне исследуемого признака | a) Две выборки испытуемых | Критерий Макнамары Q критерий Розенбаума U критерий Манна-Уитни φ - критерий (угловое преобразование Фишера) |
| b) Три и больше выборок испытуемых | S критерий Джонкира H критерий Крускала-Уоллиса | |
| Задачи | Условия | Методы |
| 2. Оценка сдвига значений исследуемого признака | a) Два замера на одной и той же выборке испытуемых | T критерий Вилкоксона G критерий знаков φ - критерий (угловое преобразование Фишера) t –критерий Стьюдента |
| b) Три и более замеров на одной и той же выборке испытуемых | критерий Фридмана L критерий тенденций Пейджа t –критерий Стьюдента | |
| 3. Выявление различий в распределении признака | a) При сопоставлении эмпирического распределения с теоретическим | χ2 критерий Пирсона λ критерий Колмогорова - Смирнова t –критерий Стьюдента |
| b) При сопоставлении двух эмпирических распределений | χ2 критерий Пирсона λ критерий Колмогорова - Смирнова φ критерий (угловое преобразование Фишера) | |
| 4. Выявление степени согласованности изменений | a) Двух признаков | φ коэффициент корреляции Пирсона η корреляционное отношение Пирсона τ коэффициент корреляции Кендела ρ коэффициент ранговой корреляции Спирмена |
Все критерии различий условно подразделены на две группы: параметрические и непараметрические критерии.
Критерий различий называют параметрическим, если он основан на конкретном типе распределения генеральной совокупности (как правило, нормальном) или использует параметры этой совокупности (средние, дисперсии и т.д.).
Критерий различий называют непараметрическим, если он не базируется на предположении о типе распределения генеральной совокупности и не использует параметры этой совокупности.
Таким образом, если вид распределения или функция распределения выборки нам заданы, то в этом случае задача оценки различий двух групп независимых наблюдений может решаться с использованием параметрических критериев статистики: либо критерия Стьюдента (t), если сравнение выборок ведется по средним значениям (X и У), либо с использованием критерия Фишера (F), если сравнение выборок ведется по их дисперсиям.
Параметрические критерии различий основываются на предположении о том, что распределение выборок подчиняется нормальному (гауссовому) закону распределения.
Нормальное распределение имеет колоколообразную форму, значения моды, медианы и среднего арифметического равны (рис. 1).
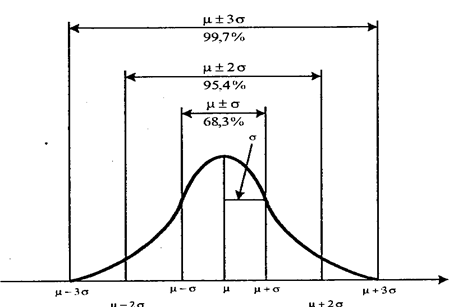
Рисунок 1 - Кривая нормального распределения с границами стандартных отклонений
Использование параметрических критериев статистики без предварительной проверки вида распределения может привести к определенным ошибкам в ходе проверки рабочей гипотезы.
Если вид распределения или функция распределения выборки нам не заданы, следует использовать непараметрические критерии статистики, например такие, как G критерий знаков, T критерий Вилкоксона, U критерий Манна-Уитни, ρ коэффициент ранговой корреляции Спирмена.
Приведем примеры наиболее часто используемых статистических критериев для решения задач исследовательской работы. Более полную информацию можно получить в учебнике: Ермолаев-Томин, О. Ю. Математические методы в психологии: учебник для бакалавров / О. Ю. Ермолаев-Томин. – 4-е изд., перераб. и доп. – М.: Издательство Юрайт, 2013. – 511 с. – Серия: Бакалавр. Базовый курс.
Критерий знаков G
Критерий знаков G позволяет установить, насколько однонаправлено изменяются значения признака при повторном изменении связанной, однородной выборки.
При вычислении критерия знаков G рассчитываются «сдвиги». Сдвиг – это величина разности между показателями выраженности какого-либо признака одного и того же участника «после» и «до» какого-либо воздействия на признак. В результате получаем нулевые, положительные и отрицательные сдвиги. В этом критерии нулевые сдвиги не учитываются.
Для решения вопроса об изменении признака вводятся понятия типичного и нетипичного сдвига.
Типичный сдвиг – это сумма сдвигов, получившая наибольшее количество значений (отрицательных или положительных).
Нетипичный сдвиг – это сумма сдвигов, получившая наименьшее количество значений (отрицательных или положительных) и обозначается как Gэмп.
Пример. Психолог проводит коррекционно-развивающие занятия с первоклассниками, направленными на развитие произвольного внимания. Его задача – выяснить будет ли эффективным вариант коррекционно-развивающей программы для развития произвольного внимания. Для решения этой задачи психолог измерил по методике «корректурная проба» количество ошибок, которые допускали ученики до и после занятий по программе.
| № п/п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| До | 24 | 12 | 42 | 30 | 40 | 55 | 50 | 52 | 50 | 22 | 33 | 78 | 79 | 25 | 12 |
| После | 22 | 12 | 41 | 31 | 32 | 44 | 50 | 32 | 32 | 21 | 34 | 56 | 78 | 23 | 18 |
| Сдвиг | -2 | 0 | -1 | 1 | -8 | -11 | 0 | -20 | -18 | -1 | 2 | -22 | -1 | -2 | 6 |
Общее число нулевых сдвигов –2;
Общее число положительных сдвигов – 3;
Общее число отрицательных сдвигов – 10.
Gэмп. = 3, так это наименьшее количество значений.
Оценка статистической достоверности различий по критерию знаков G производится по таблице критических значений для данного критерия.
Количество типичных сдвигов (n=10) показывает для какого n нужно искать критические значения критерия.
Отметим все полученные значения на оси значимости.
 | |||
 | |||
Зона незначимости
0,05 0,01
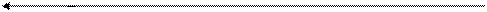
Gэмп =3 1 0
Рисунок 2 - Значения на оси значимости
Полученное эмпирическое значение критерия знаков G попало в зону незначимости, следовательно, принимается нулевая гипотеза об отсутствии различий. А это значит, что вариант коррекционно-развивающей программы психолога не оказывает существенного влияния на развитие произвольного внимания и его необходимо доработать.
F -критерий Фишера
Критерий Фишера позволяет сравнивать величины выборочных дисперсий двух независимых выборок. Для вычисления Fэмп нужно найти отношение дисперсий двух выборок, причем так, чтобы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе. Формула вычисления критерия Фишера такова:
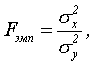(1)
где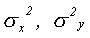 
- дисперсии первой и второй выборки соответственно.
Так как, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значение Fэмп всегда будет больше или равно единице.
Число степеней свободы определяется также просто:
k 1 =nl - 1 для первой выборки (т.е. для той выборки, величина дисперсии которой больше) и k 2 = n 2 - 1 для второй выборки.
В Приложении (см. приложение к учебникам статистики) критические значения критерия Фишера находятся по величинам k1 (верхняя строчка таблицы) и k2 (левый столбец таблицы).
Если tэмп>tкрит, то нулевая гипотеза принимается, в противном случае принимается альтернативная.
Пример 3. В двух третьих классах проводилось тестирование умственного развития по тесту ТУРМШ десяти учащихся [1]. Полученные значения величин средних достоверно не различались, однако психолога интересует вопрос — есть ли различия в степени однородности показателей умственного развития между классами.
Решение. Для критерия Фишера необходимо сравнить дисперсии тестовых оценок в обоих классах. Результаты тестирования представлены в таблице:
| №№ учащихся | Первый класс | Второй класс |
| 1 | 90 | 41 |
| 2 | 29 | 49 |
| 3 | 39 | 56 |
| 4 | 79 | 64 |
| 5 | 88 | 72 |
| 6 | 53 | 65 |
| 7 | 34 | 63 |
| 8 | 40 | 87 |
| 9 | 75 | 77 |
| 10 | 79 | 62 |
| Суммы | 606 | 636 |
| Среднее | 60,6 | 63,6 |
Рассчитав дисперсии для переменных X и Y, получаем:
s x 2 =572,83; s y 2 =174,04
Тогда по формуле (1) для расчета по F критерию Фишера находим:
По таблице из Приложения (см. приложение к учебникам статистики) для F критерия при степенях свободы в обоих случаях равных k=10 - 1 = 9 находим Fкрит=3,18 (<3.29), следовательно, в терминах статистических гипотез можно утверждать, что Н0 (гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н1. Иcследователь может утверждать, что по степени однородности такого показателя, как умственное развитие, имеется различие между выборками из двух классов.
О.Ю.Ермолаев предлагает для принятия статистического решения выделять следующие этапы.
1) Формулировка нулевой и альтернативной гипотез.
2) Определение объема выборки N.
3) Выбор соответствующего уровня значимости или вероятности отклонения нулевой гипотезы. Это может быть величина меньшая или равная 0,05 (5% уровень значимости). В зависимости от важности исследования можно выбрать уровень значимости в 0,1% или даже в 0,001%.
4) Выбор статистического метода, который зависит от типа решаемой психологической задачи.
5) Вычисление соответствующего эмпирического значения по экспериментальным данным, согласно выбранному статистическому методу.
6) Нахождение по таблице для выбранного статистического метода критических значений, соответствующих уровню значимости для Р=0,05 и для Р=0,01.
7) Построение оси значимости и нанесение на нее табличных критических значений и эмпирического значения. Для этого целесообразно пользоваться каждый раз приведенными выше рисунками.
8) Формулировка принятия решения.
ПРИЛОЖЕНИЕ 5
Дата: 2019-05-29, просмотров: 217.
