Исходные данные о геометрической форме изделия, могут поступать в САМ-систему в формате Boundary Representation (B-Rep). Изучим этот формат более подробно.
Автором были рассмотрены структуры данных геометрического ядра ACIS фирмы Spatial Technology, геометрического ядра Parasolid фирмы Unigraphics Solutions, геометрического ядра Cascade фирмы Matra Datavision и представление модели в спецификации IGES. Во всех четырех источниках представление модели очень схоже, имеются лишь небольшие отличия в терминологии, в ядре ACIS имеются непринципиальные структуры данных связанные с оптимизацией вычислительных алгоритмов. Минимальный список объектов, необходимый для представления B-Rep модели представлен на Рис. 1. Его можно разделить на две группы. В левом столбце представлены геометрические объекты, а в правом топологические.
Рис. 1. Геометрические и топологические объекты.
Геометрическими объектами являются поверхность (Surface), кривая (Curve) и точка (Point). Они самостоятельны и не ссылаются на другие составляющие модели, именно они определяют пространственное расположение и размеры геометрической модели.
Топологические объекты описывают то, каким образом геометрические соединяются в пространстве. Сама по себе топология описывает структуру или сетку, которая никоим образом не зафиксирована в пространстве.
Кривые и поверхности . Как известно, существуют два наиболее общих метода представления кривых и поверхностей. Это неявные уравнения и параметрические функции.
Неявное уравнение кривой лежащей в плоскости xy имеет вид:
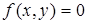
Это уравнение описывает неявное отношение между координатами x и y точек лежащих на кривой. Для данной кривой уравнение уникально. Например, окружность с единичным радиусом и центром в начале координат, описывается уравнением
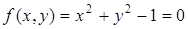
В параметрической форме, каждая из координат точки кривой представляется отдельно как явная функция параметра:
,
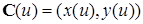где: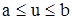 
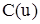- векторная функция от параметра u.
Хотя интервал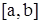 
произвольный, он обычно нормализуется до 
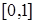. Первый квадрант окружности описывается параметрическими функциями:
,
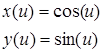где: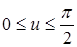 
.
Установим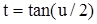 
, получим другое представление:
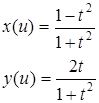
где: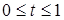 
.
Таким образом, представление кривой в параметрическом виде не уникально.
Поверхность также может быть представлена неявным уравнением в форме:
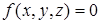
Параметрическое представление (не уникальное) дается как:
.
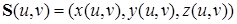Заметим, что для описания поверхности необходимы два параметра. Прямоугольную область существования всей совокупности точек (u,v), ограниченную условиями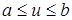 
и 
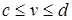будем называть областью или плоскостью параметров. Каждой точке в области параметров будет соответствовать точка на поверхности в модельном пространстве.
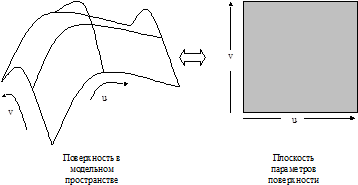
Рис. 2. Параметрическое задание поверхности.
Зафиксировав u и изменяя v, получаем поперечные линии, зафиксировав v и изменяя u, получаем продольные линии. Такие линии называют изопараметрическими.
Для представления кривых и поверхностей внутри B-Rep модели наиболее удобна параметрическая форма.
Топологические объекты . Тело ( Body) - это ограниченный объем V в трехмерном пространстве. Тело будет корректным в том случае, если этот объем замкнутый и конечный. Тело может состоять из нескольких, не касающихся друг друга кусочков (Lumps), доступ к которым необходимо обеспечить как к единому целому. На рисунке изображен пример тела состоящего из более чем одного кусочка.
Рис. 3. Четыре кусочка в одном теле
Кусочек (Lump) – это единая область в трехмерном пространстве, ограниченная одной или более оболочками (Shells). Lump может иметь неограниченное количество пустот. Таким образом, одна оболочка кусочка является внешней, остальные внутренними.
Рис. 4. Тело, состоящее из двух кусочков
Оболочка ( Shell) – это множество ограниченных поверхностей (Faces), объединенных между собой посредством общих вершин (Vertexes) и ребер (Edges). Нормали к поверхностям оболочки должны быть направлены от зоны существования тела. Ограниченная поверхность ( Face) - это участок обычной геометрической поверхности, ограниченный одной или несколькими замкнутыми последовательностями кривых – петлями (Loops). При этом петля может задаваться кривыми, как в модельном, так и в параметрическом пространстве поверхности. Ограниченная поверхность в своей сути является двухмерным аналогом тела. Она также может иметь одну внешнюю и множество внутренних зон ограничений.
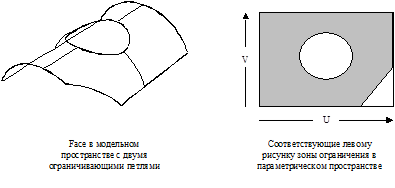
Рис. 5. Ограниченная поверхность
Петля (Loop) – является участком зоны ограничения Face. Она представляет собой множество параметрических ребер объединенных в двухсвязную цепочку. Для корректного тела она должна быть замкнутой.
Параметрическое ребро (Coedge) – это запись, соответствующая участку петли. Оно соответствует ребру геометрической модели. Параметрическое ребро имеет ссылку на двухмерную геометрическую кривую, соответствующую участку зоны ограничения в параметрическом пространстве. Параметрическое ребро ориентировано в петле таким образом, что если смотреть вдоль ребра по его направлению, то зона существования поверхности будет находиться слева от него. Таким образом, внешняя петля всегда направлена против часовой стрелки, а внутренние по часовой.
Параметрическое ребро ( Coedge) может иметь ссылку на партнера, на такой же Coedge, лежащий в другой петле, но соответствующий тому же пространственному ребру. Поскольку в корректном теле, каждое ребро касается строго двух поверхностей, поэтому оно будет иметь строго два параметрических ребра.
Рис. 6. Ребра, параметрические ребра и вершины
Ребро ( Edge) – топологический элемент, имеющий ссылку на трехмерную геометрическую кривую. Ребро ограничено с обеих сторон вершинами.
Вершина (Vertex) – топологический элемент, имеющий ссылку на геометрическую точку (Point). Вершина –это граница ребра. Все другие ребра, которые приходят в конкретную вершину, могут быть найдены через указатели параметрических ребер.
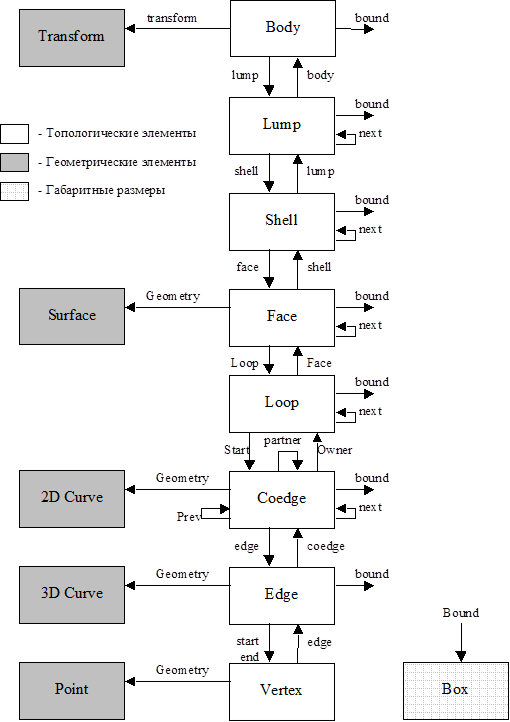
Рис. 7. Объектная реализация геометрической модели
В данной диаграмме фигурируют еще два неописанных объекта.
Система координат тела ( Transform). Как известно система координат может задаваться матрицей преобразований. Размерность матрицы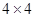 
. Если координаты точки представить в виде вектора-строки, в последнем столбце которого лежит единица, то умножив этот вектор на матрицу преобразований получим координаты точки в новой системе координат.
Матрица может отражать в себе все пространственные преобразования, такие как: поворот, перенос, симметрия, масштабирование и их композиции. Как правило, матрица имеет следующий вид.
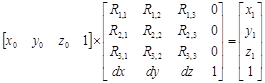
Габаритные размеры ( Box) – структура данных, описывающая параметры прямоугольного параллелепипеда со сторонами параллельными координатным осям. Фактически это координаты двух точек, расположенных на концах главной диагонали параллелепипеда.
Кривые и поверхности NURBS
В настоящее время наиболее распространенным способом представления кривых и поверхностей в параметрической форме являются рациональные сплайны или NURBS (non-uniform rational b-spline). В виде NURBS с абсолютной точностью могут быть представлены такие канонические формы как отрезок, дуга окружности, эллипс, плоскость, сфера, цилиндр, тор и другие, что позволяет говорить об универсальности данного формата, и исключает необходимость использования иных способов представления.
Кривая в таком виде описывается следующей формулой:
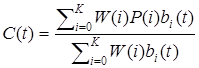
Здесь
· W(i) - весовые коэффициенты (положительные действительные числа),
· P(i) - контрольные точки,
· Bi - B-сплайновые функции
В-сплайновые функции степени М полностью определяются множеством узлов. Пусть N=K-M+1, то множество узлов представляет собой последовательность не уменьшающихся действительных чисел:
T(-M),…,T(0),…,T(N),…T(N+M).
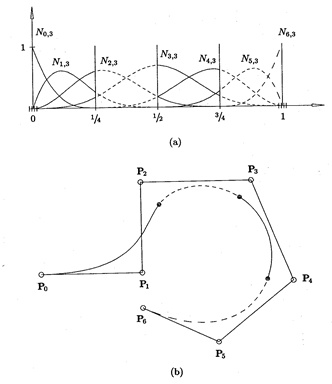
Рис. 8. (a) кубические базисные функции ; (b) кубическая кривая, использующая базисные функции с (a)
Сегмент кривой, представленной в виде NURBS, может быть преобразован в полиномиальную форму без потери точности, то есть представлен выражениями:
,
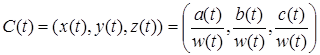где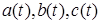 
и 
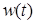являются полиномами степени кривой. Способы преобразования кривых из NURBS в полиномиальную форму и обратно подробно описаны в /1/.
Поверхности NURBS представляются аналогичным образом:
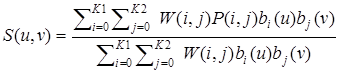
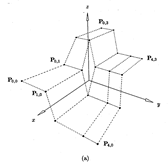
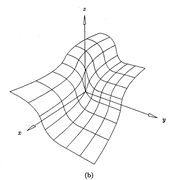
Рис. 9. В-сплайновая поверхность: (a) сетка контрольных точек; (b) поверхность
Как видно из рисунков, сложность геометрической формы кривой или поверхности можно оценить по контрольным точкам.
Сегмент поверхности NURBS также может быть представлен в полиномиальной форме:
,
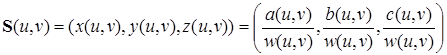где 
и 
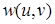являются полиномами двух переменных и могут быть представлены в виде:
.
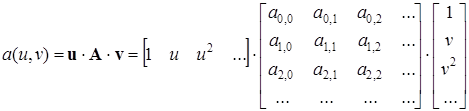Более подробно свойства NURBS кривых и поверхностей описаны в /1,2/.
Для любой двумерной параметрической кривой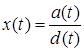 
, 
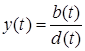, где 
, 
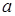и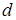 
- полиномы существует уравнение 
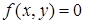, где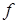 
также полином, которое точно определяет ту же самую кривую. Для любой параметрической поверхности заданной выражением (6) существует уравнение 
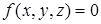, где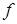 
также полином, которое точно определяет ту же самую поверхность. Способы получения неявной формы параметрически заданной кривой или поверхности описаны в /33/.
Дата: 2019-05-29, просмотров: 242.
