Для двоичного счётчика, т.е. счётчика с Ксч=2m, зная номера триггеров и состояния выходов Q, можно определить записанное в счётчик двоичное число
M = Qm*2m-1 + Qm-1*2m-2 +... + Q1*20, где m – номер триггера.
Двоичный асинхронный счётчик может состоять из Т-триггеров, соединённых последовательно так, что выход последнего триггера соединён с тактовым входом последующего.
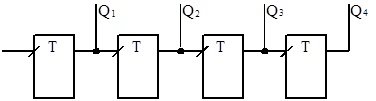
Рис.2.1 Двоичный асинхронный счётчик.
Асинхронным счётчик называют потому, что в тех случаях, когда с приходом очередного счётного импульса срабатывают сразу несколько триггеров, опрокидываются они не одновременно, а с некоторой задержкой относительно друг друга. Если, например, все четыре триггера в счётчике находятся в единице, то очередной входной импульс опрокинет первый триггер, изменение потенциала на выходе приведет к опрокидыванию второго триггера, затем опрокинется третий и уже после этого четвёртый. Это вызывает не только задержку в установлении соответствующего кода после прихода счётного импульса, но и появление коротких ложных импульсов. Так как переход 1111–0000 осуществляется через кратковременные промежуточные состояния 1110–1100–1000.
При поступлении счётных импульсов триггеры счётчика проходят состояния, состояния описываемые последовательно возрастающими двоичными числами:
Таблица 2.1
Состояние триггеров счетчика при поступлении счетных импульсов.
| n | Q4 | Q3 | Q2 | Q1 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| ... | ... | ... | ... | ... |
| 15 | 1 | 1 | 1 | 1 |
Как было показано выше, Т-триггер может быть образован из любых других триггеров по описанным правилам коммутаций, которые при изложении работы счётчиков будем опускать для упрощения анализа схемных решений.
Двоичный синхронный счётчик (с параллельным переносом)
В этих счётчиках счётные импульсы подаются одновременно на тактовые выходы всех триггеров счётчика, при этом схема построена так, что каждому импульсу соответствует срабатывание только определённых триггеров. Из-за этого обеспечивается большее быстродействие.
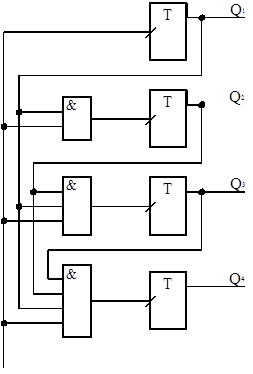
Рис.2.2 Двоичный синхронный счётчик.
В таких счётчиках используют JK - и D-триггеры, часто со встроенными логическими элементами.
В схемном отношении эти счётчики сложнее асинхронных счётчиков, так как требуют применения кроме триггеров и логических элементов.
Счётчики с недвоичным коэффициентом пересчёта
Введением дополнительных логических связей – обратных и прямых – двоичные счётчики могут быть обращены в недвоичные, для которых Ксч ¹ 2m.
Синтез счётчиков с заданным коэффициентом счёта сводится к нахождению логических функций, которым должны соответствовать сигналы, присутствующие на управляющих входах триггеров.
Синтез синхронного счётчика
Порядок синтеза рассмотрим на примере двоично-десятичного счётчика, работающего в коде 8-4-2-1.
Сначала синтезируют таблицу кодовых комбинаций соответствующих различным состояниям этого счётчика. Переход от одного состояния к другому осуществляется под воздействием счётных импульсов n, поступающих одновременно на тактовые входы всех четырёх триггеров.
К приходу очередного счётного импульса на управляющих входах триггеров должны существовать сигналы, обеспечивающие срабатывание только тех триггеров, которые должны изменить своё состояние при переходе к следующей кодовой комбинации.
Таким образом, для каждой кодовой группы, характеризующей состояние счётчика, необходимо найти сигналы на управляющих входах триггеров, обеспечивающих переход к следующей кодовой группе.
Пусть, этот счётчик требуется построить на JK-триггерах, которые работают так, что:
Если такой триггер должен перейти из нуля в единицу, то к приходу счётного импульса на тактовый вход нужно обеспечить J=1, сигнал на входе К не влияет при этом на поведение триггера и может быть либо 0, либо 1, т.е. К=Х;
Если триггер должен опрокинуться из единицы в ноль, следует к приходу счётного импульса установить К=1, J=Х (сигнал на входе J не влияет при этом на поведение триггера);
Если же требуется сохранить состояние триггера “единица”, то необходимо к приходу счётного импульса установить К=0, J=X;
Если триггер должен остаться в состоянии ноль, то нужно обеспечить J=0, K=X.
В таблице указывают значения сигналов, которые должны быть поданы на управляющие JK-входы триггеров, для того чтобы обеспечить переход от данного состояния счётчика к последующему.
Таблица 2.2
Кодовые комбинации
| счетный импульс | Состояние счетчика | Значения сигналов на управляющих входах триггеров | ||||||||||
| Q4 | Q3 | Q2 | Q1 | 4 | 3 | 2 | 1 | |||||
| n | J4 | K4 | J3 | K3 | J2 | K2 | J1 | K1 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | x | 0 | x | 0 | x | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | x | 0 | x | 1 | x | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 | x | 0 | x | x | 0 | 1 | 1 |
| 3 | 0 | 0 | 1 | 1 | 0 | x | 1 | x | x | 1 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 | x | x | 0 | 0 | x | 1 | 1 |
| 5 | 0 | 1 | 0 | 1 | 0 | x | x | 0 | 1 | x | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 0 | x | x | 0 | x | 0 | 1 | 1 |
| 7 | 0 | 1 | 1 | 1 | 1 | x | x | 1 | x | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 | x | 0 | 0 | x | 0 | x | 1 | 1 |
| 9 | 1 | 0 | 0 | 1 | x | 0 | 0 | x | 1 | x | 1 | 1 |
| 10 | 0 | 0 | 0 | 0 | ||||||||
Из анализа кодовых комбинаций для первого триггера видно, что он работает в режиме простого деления на два. Такой режим работы обеспечивается при J1=1, K1=1.
Данные из таблицы переносят на карты Карно с тем, чтобы провести минимизацию функции, определяющей каждый из управляющих сигналов триггеров, и затем составит логическую цепь, реализующую полученную функцию.
В этих картах по шесть клеток не заполнены: эти клетки соответствуют неиспользованным кодовым комбинациям. Совокупность четырех триггеров может находиться в одном из шестнадцати состояний (24=16), из которых в счётчике используются десять.
Карты Карно для управляющих сигналов:
K2: J2:
| Q2Q1 Q4Q3 | 00 | 01 | 11 | 10 | Q2Q1 Q4Q3 | 00 | 01 | 11 | 10 | |
| 00 | X |  X X
| 1 | 0 | 00 | 0 |  1 1
| X | X | |
| 01 | X | X | 1 | 0 | 01 | 0 | 1 | X | X | |
| 11 | 11 | |||||||||
| 10 | X | X | 10 | 0 | 1 |
K2 = Q1 J2 = Q1 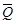 4
4
K3: J3:
| Q2Q1 Q4Q3 | 00 | 01 | 11 | 10 | Q2Q1 Q4Q3 | 00 | 01 | 11 | 10 | |
| 00 | X | X |  X X
| 0 | 00 | 0 | 0 |  1 1
| 0 | |
| 01 | 0 | 0 | 1 | 0 | 01 | X | X | X | X | |
| 11 | 11 | |||||||||
| 10 | X | X | 10 | 0 | 0 |
K3 = Q1Q2 J3 = Q1Q2
K4: J4:
| Q2Q1 Q4Q3 | 00 | 01 | 11 | 10 | Q2Q1 Q4Q3 | 00 | 01 | 11 | 10 | |
| 00 | X | X | X | 0 | 00 | 0 | 0 | 0 | 0 | |
| 01 | X | X | X | X | 01 | 0 | 0 |  1 1
| 0 | |
| 11 | 11 | |||||||||
| 10 | 0 | 0 | 10 | 0 | 0 |
K4 = 0 J4 = Q1Q2Q3
Рис 2.3 Карты Карно для управляющих сигналов.
Часть клеток 1 таблице заполнена символом Х, что означает, что минимизируемая функция может при данном наборе аргументов Q1–Q4, принимать любое значение – 0 или 1. Определённые значения функции в таблице заменены 0 или 1.
Особенностью минимизации логических функций, значение которых при определённых наборах аргументов не играет роли (не заполненные клетки и клетки с символом Х), является то, что при проведении в картах контуров, охватывающих единицы, можно включать в эти контуры также и клетки, в которых функция не определена.
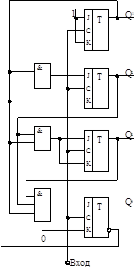
Рис.2.4 Функциональная схема двоично-десятичного счётчика.
Для указанных в таблице контуров:
K2 = Q1J2 = Q1 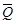 4
4
K3 = Q1Q2J3 = Q1Q2
K4 = 0J4 = Q1Q2Q3
Функциональная схема счётчика синтезируется в соответствии с полученными логическими функциями.
Аналогичным образом проводят синтез счётчиков на других типах триггеров тактируемых фронтом импульса и с другими коэффициентами пересчёта. Различие будет заключаться в сигналах, обеспечивающих нужные переходы или сохранение состояний триггеров.
Дата: 2019-05-29, просмотров: 369.