Задача коммивояжера (в дальнейшем сокращённо - ЗК) является одной из знаменитых задач теории комбинаторики. Она была поставлена в 1934 году, и об неё, как об Великую теорему Ферма обламывали зубы лучшие математики. В своей области (оптимизации дискретных задач) ЗК служит своеобразным полигоном, на котором испытываются всё новые методы. Ниже будет показано, что решение ЗК методом полного перебора оказывается практически неосуществимым даже для сравнительно небольших задач. Более того, известно, что ЗК принадлежит к числу NP-полных задач.

Общее описание

Постановка задачи следующая.

Коммивояжер (бродячий торговец) должен выйти из первого города, посетить по одному разу в неизвестном порядке города 1,2,3..n и вернуться в первый город. Расстояния между городами известны. В каком порядке следует обходить города, чтобы замкнутый путь (тур) коммивояжера был кратчайшим?

Чтобы привести задачу к научному виду, введём некоторые термины. Итак, города перенумерованы числами jÎТ=(1,2,…,n). Тур коммивояжера может быть описан циклической перестановкой t=(j₁,…,j_n, j₁), причём все j₁,…,j_n – разные номера; повторяющийся в начале и в конце j₁, показывает, что перестановка зациклена. Расстояния между парами вершин С_ij образуют матрицу С. Далее введем n² альтернативных переменных x_ij, принимающих значение 0, если переход из i-го пункта в j-ый не входит в маршрут и 1 в противном случае. Условия прибытия в каждый пункт и выхода из каждого пункта только по одному разу выражаются равенствами (1) и (2).

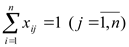(1)

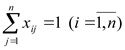(2)

Для обеспечения непрерывности маршрута вводятся дополнительно n переменных 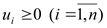и n² дополнительных ограничений 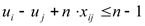(3).

(3)

Задача состоит в том, чтобы найти такой тур t, чтобы минимизировать суммарную протяженность маршрута F, которая запишется в следующем виде:

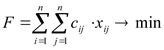(4)

Относительно математической формулировки ЗК уместно сделать два замечания. Первое, в постановке С_ij означали расстояния, поэтому должны выполняться следующие условия:

o неотрицательными, т.е. для всех jÎТ:

C_ij ³ 0;

C_jj = ∞ (5)

(последнее равенство означает запрет на петли в туре),

o симметричными, т.е. для всех i, j:

С_ij = С_ji (6)

o удовлетворять неравенству треугольника, т.е. для всех:

C_ij + C_jk ³ C_ik (7)

В математической постановке говорится о произвольной матрице. Сделано это потому, что имеется много прикладных задач, которые описываются основной моделью, но всем условиям (5)-(7) не удовлетворяют. Особенно часто нарушается условие (7) (например, если С_ij – не расстояние, а плата за проезд: часто туда билет стоит одну цену, а обратно – другую). Поэтому мы будем различать два варианта ЗК: симметричную задачу, когда условие (7) выполнено, и несимметричную - в противном случае. Условия (5)-(7) по умолчанию мы будем считать выполненными.

Второе замечание касается числа всех возможных туров. В несимметричной ЗК все туры t=(j₁,j₂,…,j_n,j₁) и t’=(j₁,j_n,…,j₂,j₁) имеют разную длину и должны учитываться оба. Всего разных туров очевидно (n-1)!

Зафиксируем на первом и последнем месте в циклической перестановке номер j₁, а оставшиеся n-1 номеров переставим всеми (n-1)! возможными способами. В результате получим все несимметричные туры. Симметричных туров имеется в два раз меньше, т.к. каждый засчитан два раза: как t и как t’.

Можно представить, что X состоит только из единиц и нулей. Тогда С можно интерпретировать, как граф, где ребро (i,j) проведено, если x_ij=0 и не проведено, если x_ij=1. Тогда, если существует тур длины 0, то он пройдёт по циклу, который включает все вершины по одному разу. Такой цикл называется гамильтоновым циклом. Незамкнутый гамильтонов цикл называется гамильтоновой цепью (гамильтоновым путём).

Доказательство, что модель (1-4) описывает задачу о коммивояжере.

Условие (2) означает, что коммивояжер из каждого города выезжает только один раз; условие (3) - въезжает в каждый город только один раз; условие (4) - обеспечивает замкнутость маршрута, содержащего N городов, и не содержащего замкнутых внутренних петель.

Рассмотрим условие (4) подробнее. Применим метод доказательства от противного, то есть предположим, что условие (4) выполняется для некоторого подцикла T из R городов, где R

.

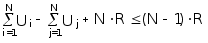Так как

,

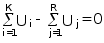то N·R £ (N -1), где R < N, R ¹ 0.

Следовательно, не существует замкнутого подцикла с числом городов меньшим, чем N.

Покажем, что существует U_i, которое для замкнутого цикла, начинающегося в некотором начальном пункте, удовлетворяют условию (4). При всех X_ij (j-й город не посещается после i-го) в (4) имеем U_i-U_j £ N-1, что допустимо в силу произвольных U_i и U_j.

Пусть на некотором R-ом шаге i-й город посещается перед j-м, то есть X_ij = 1. В силу произвольности значений U_i и U_j положим U_i = R, а U_j = R+1, тогда из (4) имеем:

U_i-U_j+N·X_ij £ R-(R-1)+N = N-1

Итак, существуют такие конечные значения для U_i и U_j, что для маршрута, содержащего N городов, условие (4) удовлетворяется как неравенство или строгое равенство. А следовательно, модель (1)-(4) описывает задачу о коммивояжере.

В терминах теории графов симметричную ЗК можно сформулировать так:

Дана полная сеть с n вершинами, длина ребра (i,j)= С_ij. Найти гамильтонов цикл минимальной длины.

В несимметричной ЗК вместо «цикл» надо говорить «контур», а вместо «ребра» - «дуги», «стрелки».

Некоторые прикладные задачи формулируются как ЗК, но в них нужно минимизировать длину не гамильтонова цикла, а гамильтоновой цепи. Такие задачи называются незамкнутыми. Некоторые модели сводятся к задаче о нескольких коммивояжерах, но мы здесь их рассматривать не будем.

Жадный” алгоритм решения ЗК

Жадный алгоритм – алгоритм нахождения наикратчайшего расстояния путём выбора самого короткого, ещё не выбранного ребра, при условии, что оно не образует цикла с уже выбранными рёбрами. “Жадным” этот алгоритм назван потому, что на последних шагах приходится жестоко расплачиваться за жадность.

П осмотрим, как поведет себя при решении ЗК жадный алгоритм. Здесь алгоритм превратится в стратегию “иди в ближайший, в который еще не входил, город”. Жадный алгоритм, очевидно, бессилен в этой задаче. Рассмотрим для примера сеть на рис. 2, представляющую узкий ромб. Пусть коммивояжер стартует из города 1. Алгоритм “иди вы ближайший город” выведет его в город 2, затем 3, затем 4; на последнем шаге придется платить за жадность, возвращаясь по длинной диагонали ромба. В результате получится не кратчайший, а длиннейший тур.

В пользу процедуры “иди в ближайший” можно сказать лишь то, что при старте из одного города она не уступит стратегии “иди в дальнейший”.

Как видим, жадный алгоритм ошибается. Можно ли доказать, что он ошибается умеренно, что полученный им тур хуже минимального, положим, в 1000 раз? Мы докажем, что этого доказать нельзя, причем не только для жадного алгоритма, а для алгоритмов го­раздо более мощных. Но сначала нужно договориться, как оценивать погрешность неточных алгоритмов, для определенности, в задаче минимизации. Пусть f_B - настоящий минимум, а f_A - тот квазиминимум, который получен по алгоритму. Ясно, что f_A/ f_B≥1, но это – тривиальное утверждение, что может быть погрешность. Чтобы оценить её, нужно «зажать» отношение оценкой сверху:

f_A/f_B ≥ 1+nε (8)

где, как обычно в высшей математике, ε≥0, но, против обычая, может быть очень большим. Величина ε и будет служить мерой погрешности. Если алгоритм минимизации будет удовлетворять неравенству (8), мы будем говорить, что он имеет погрешность ε.

Предположим теперь, что имеется алгоритм А решения ЗК, погрешность которого нужно оценить. Возьмем произвольный граф G(V,E) и по нему составим входную матрицу ЗК:

Если в графе G есть гамильтонов цикл, то минимальный тур проходит по этому циклу и f_B = n. Если алгоритм А тоже всегда будет находить этот путь, то по результатам алгоритма можно судить, есть ли гамильтонов цикл в произвольном графе. Однако, не переборного алгоритма, который мог бы ответить, есть ли гамильтонов цикл в произвольном графе, до сих пор никому не известно. Таким образом, наш алгоритм А должен иногда ошибаться и включать в тур хотя бы одно ребро длины 1+nε. Но тогда f_A ³ (n-1)+(1+nε) так что f_A/f_B = 1+nε, т.е. превосходит погрешность ε на заданную неравенством (8). О величине ε в нашем рассуждении мы не договаривались, так что ε может быть произвольно большим.

Таким образом доказана следующая теорема.

Либо алгоритм А определяет, существует ли в произвольном графе гамильтонов цикл, либо погрешность А при решении ЗК может быть произвольно велика.

Это соображение было впервые опубликовано Сани и Гонзалесом в 1980 г. Теорема Сани-Гонзалеса основана на том, что нет никаких ограничений на длину ребер. Теорема не проходит, если расстояния подчиняются неравенству треугольника (7).