Класс.
Глава I .
Точки, прямые, отрезки.
Через любые две точки Если две прямые имеют общую
можно провести прямую, точку, то они пересекаются.
и притом только одну.
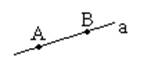
Прямая а и точки А и В.
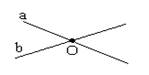
Прямая а и b пересекаются в точке О.
Две прямые либо имеют только одну общую точку,
либо не имеют общих точек.
Угол.
Угол – это геометрическая фигура, Угол называется развёрнутым, которая состоит из точки и двух лучей, если обе его стороны
исходящих из этой точки. лежат на одной прямой.
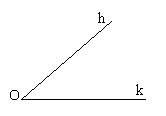
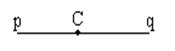
Угол с вершиной О и сторонами h и k. Развёрнутый угол с вершиной С
и сторонами p и q.
Развёрнутый угол = 180º; Неразвёрнутый угол < 180º .
Луч, исходящий из вершины угла и Два угла, у которых одна общая
делящий его на два равных угла, сторона общая, а две другие
называется биссектриса угла. являются продолжениями одна
другой, называются смежными.
Два угла, называются вертикальными,
если стороны одного угла являются Сумма смежных углов = 180º.
продолжениями сторон другого.
Две пересекающиеся прямые
Вертикальные углы равны. называются перпендикулярными,
если они образуют 4 прямых угла.
Глава I I.
Треугольники.
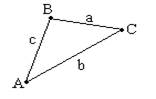
Треугольник – геометрическая фигура, Р АВС = АВ+ВС+СА.
кот-ая состоит из 3 точек, не лежа-
щих на 1 прямой, соединённых отрезками.
В равных треугольниках против
Треугольник с вершинами А, В, С и соответственно равных сторон
Сторонами а, b, c. лежат равные углы, также против
соответственно равных равных
углов лежат равные стороны.
Теорема: Если 2 стороны и угол Теорема: Из точки, не лежа-
между ними 1-го треугольника щей на прямой, можно провести
соответственно равны 2 сторонам перпендикуляр к этой, и притом
И углу между ними другого только один.
треугольника, то треугольники равны.
Отрезок, соединяющий вершину треуг- Отрезок бисс-сы угла треуг-ка,
ка с серединой противоположной сто- соединяющий вершину треуг-ка
роны, называется медианой треуг-ка. с точкой противоположной сторо- ны, называется бисс-сой треуг-ка.
Перпендикуляр, проведённый из верши-
ны треуг-ка к прямой, содержащей Треуг-к, у кот-го 2 стороны равны,
противоположную сторону, называ- называется равнобедренным.
ется высотой треуг-ка.
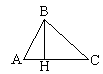Теорема: В равнобедренном треуг-ке
ВН - высота треуг-ка АВС. углы при основании равны.
Теорема: В равнобедренном Высота равнобедренного треуг-ка, про-
треуг-ке бисс-са, проведённая ведённая к основанию, является медианой
к основа-нию, является и бисс-сой.
Медианой и высотой.
Медиана, проведённая к основанию, явля-
ется высотой и бисс-сой.
Теорема: Если сторона и 2 Теорема: Если три стороны 1го
Прилежащих к ней угла 1го треуг-ка соответственно равны 3ём
Глава I I I.
Параллельные прямые.
Определение: Две прямые Теорема: Если при пересечении 2 пря-
Секущей, то соответствен-
Ные углы равны.
Глава IV.
Соотношения между сторонами
И углами треугольника.
Теорема: Сумма углов Внешний угол треуг-ка = сумме двух углов тре-
треуг-ка = 180º. уг-ка, не смежных с ним.
В любом треугольнике либо Теорема: В треуг-ке против большей сто-
все углы острые, либо два роны лежит больший угол, против большего
два угла острые, а третий угла лежит большая сторона.
тупой или прямой.
В прямоугольном треуг- ке гипотенуза Если два угла треуг-ка равны, то больше катета. треуг-к – равнобедренный.
Теорема: Каждая сторона Для любых 3 точек А,В,С, не лежащих на
треугольника меньше суммы одной прямой, справедливы неравенства:
2 других сторон. АВ< AB + BC , ВС<ВА+АС, АС<АВ+ВС.
Сумма двух острых углов пря- Катет прямоугольного треуг-ка, лежащий
моугольного треуг-ка = 90º. против угла в 30º, равен ½ гипотенузы.
Если катет прямоугольного треуг- Если катеты 1го прямоугольного треуг-
ка = ½ гипотенузы, то угол, лежа- ка соответственно = катетам другого
щий против этого катета, = 30º. , то такие треуг-ки равны.
Если катет и прилежащий к нему Теорема: Если гипотенуза и острый
острый угол 1го прямоугольного угол 1го прямоугольного треуг-ка соот-
треуг-ка соответственно равны ветственно равны гипотенузе и остро-
катету и прилежащему к нему му углу другого, то такие треуг-ки равны. острому углу другого, то такие
треугольники равны. Теорема: Если гипотенуза и катет 1го
прямоугольного треуг-ка соответствен-
Теорема: Все точки каж- но равны гипотенузе и катету другого,
Глава V .
Многоугольники.
Сумма углов выпуклого n -угольника В параллелограмме противоположные
= ( n -2)180º. стороны равны и противоположные
углы равны.
Диагонали параллелограмма точ-
кой пересечения делятся пополам. Если в 4-угольнике 2 стороны равны и
параллельны, то этот 4-угольник – па-
раллелограм.
Если в 4-угольнике противопо-
ложные стороны попарно равны, Если в 4-угольнике диагональю пересе-
то этот 4-угольник – параллело- каются и точкой пересечения делятся
грамм. пополам, то этот 4-угольник – парал-
лелограмм.
Трапецией называется 4-угольник,
у кот-го 2 стороны параллельны, а Прямоугольником называется парал-
2 другие стороны не параллельны. лелелограмм, у кот-го все углы прямые.
Диагонали прямоугольника равны. Если в параллелограмме дигонали равны,
то этот параллелограмм – прямоуголь-
Ромбом называется параллело- ник.
грамм, у кот-го все стороны
равны. Диагонали ромба взаимно перпендикуляр-
ны и делят его углы пополам.
Квадкатом называется прямо-
угольник, у кот-го все стороны Все углы квадрата равны.
равны.
Диагонали квадрата равны, взаимно
Фигура называется симметричной перпендикулярны, точкой пересечения
относительно прямой а, если для делятся пополам и делят углы
каждой точки фигуры симметричная квадрата пополам.
ей точка относительно прямой а
также принадлежит этой фигуре. Прямая а называется осью симметрии.
Фигура называется симметричной Точка О называется центром симмет-
относительно точки О, если для рии фигуры.
каждой точки фигуры симметрич-
ная ей точка относительно точки О
также принадлежит этой фигуре.
Глава VI .
Площадь.
Равные многоугольники имеют S квадрата равна квадрату его стороны.
Равные S .
Если многоугольник составлен из Теорема: S прямоугольника = про-
нескольких многоугольников, то изведению его смежных сторон.
Его S = сумме площадей этих
многоугольников. Теорема: S параллелограмма = про-
изведению его основания на высоту.
Теорема: S треугольника =
= произведению его основания S прямоугольного треугольника = 1/2
на высоту. произведения его катетов.
Если высоты 2ух 3-угольников Теорема: Если угол 1го 3-угольника
равны, то их S относятся равен углу другого 3-угольника, то S
как основания. этих 3-угольников относятся как про-
изведения сторон, заключающих равные
Теорема: S трапеции = про- углы.
Угольник прямоугольный.
Глава VII .
Подобные треугольники.
Определение: 2 3-угольника Теорема: Отношение S 2ух подоб-
называются подобными, если их ных 3-угольников = квадрату коэф-
Угольники подобны.
sin острого угла прямоугольного cos острого угла прямоугольного 3-уголь-
3-угольника – отношение ника – отношение прилежащего катета
противолежащего катета к к гипотенузе.
гипотенузе.
tg угла = отношению sin к cos
tg острого угла прямоугольного этого угла: tg = sin / cos .
3-угольника – отношение противо-
лежащего катета к прилежащему. Основное тригонометрическое
тождество:
Если острый угол 1го прямоугольного sin 2 α+ cos 2 α=1.
3-угольника = острому углу другого прямо-
угольного 3-угольника, то синусы, косинусы и тангенсы этих углов равны.
| x | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° | 180 ° | 270 ° | 360 ° |
| sinx | 0 | 1/2 | 2/2 | 3/2 | 1 | 0 | -1 | 0 |
| cosx | 1 | 3/2 | 2/2 | 1/2 | 0 | -1 | 0 | 1 |
| tgx | 0 | 1/ 3 | 1 | 3 | — | 0 | — | 0 |
| ctgx | — | 3 | 1 | 1/ 3 | 0 | — | 0 | — |
| 0 | П /6 | П/4 | П/3 | П/2 | П | 3П/2 | 2П |
Глава VIII .
Окружность.
Если расстояние от центра окруж- Если расстояние от центра окруж-
ности до прямой < радиуса, то пря- ности до прямой = радиуса, то пря-
мая и окружность имеют 2 общие мая и окружность имеют 2 общие
точки. Прямая является секущей. точки. Прямая является касательной.
Если расстояние от центра окруж- Теорема: Касательная к окруж-
ности до прямой > радиуса, то пря- ности перпендикулярна к r , прове-
мая и окружность не имеют общих дённому в точку касания.
точек.
Теорема: Если прямая проходит
Отрезки касательных к окружнос- через конец r , лежащий на окруж-
ти, проведённые из 1ой точки, рав- ности, и перпендикулярна к этому
ны и составляют равные углы с r , то она является касательной.
прямой, проходящей через эту точ-
ку и центр окружности. Дуга является полуокружностью.
Угол с вершиной в центре окруж- Если дуга АВ окружности с центром
ности — её центральный угол. О < полуокружности или является
полуокружностью, то её градусная
Сумма градусных мер 2ух дуг ок- мера считается равной градусной
ружности с общими концами = мере центрального угла АОВ. Если же
= 360°. дуга АВ > полуокружности, то её
градусная мера считается =
Угол, вершина кот-го лежит на = 360°–<АОВ.
окружности, а стороны пересе-
кают окружность, называется Теорема: Вписанный угол измеряя-
вписанным углом. ется ½ дуги, на кот-ую он опирается.
Луч ВО совпадает с 1ой из сто- Луч ВО делит угол АВС на 2 угла, если
рон угла АВС. луч ВО пересекает дугу АС.
Луч ВО не делит угол АВС на 2 Вписанные углы, опирающиеся на 1 и ту
угла и не совпадает со сторона- же дугу, равны.
ми этого угла, если луч ВО не
пересекает дугу АС. Вписанный угол, опирающийся на полу-
окружность, -- прямой.
Теорема: Если 2 хорды ок- Теорема: Каждая точка бисс-сы
Рединного перпендикуляра к
отрезку равноудалена от концов Серединные перпендикуляры к сторо-
этого отрезка. Каждая точка, нам 3-угольника пересекаются в 1ой
равноудалённая отконцов отрез- точке.
Ность.
Если сумма противоположных углов 4-угольника = 180°, то около него можно описать окружность.
Глава IX .
Векторы.
Физические величины, характери- Определение: Отрезок, для кот-
зуещиеся направлением в прост- го указано, какой из его концов счи-
ранстве – векторные. тается началом, а какой – концом,
называется вектором.
Длина (модуль) – длина АВ.
Длина нулевого вектора = 0.
Нулевые векторы называются
коллинеарными, если они лежат Если 2 вектора направлены одинаково,
либо на одной прямой, либо на то эти векторы – сонаправлены.
параллельных прямых; нулевой
вектор считается коллинеар- Если 2 вектора направлены противопо-
ным любому вектору. ложно, то они противоположно напра-
влены.
Определение: Векторы,
называются равными, если От любой точки М можно отложить
они сонаправлены и их дли- вектор, равный данному вектору ã, и
ны равны. притом только один.
Теорема: для любых векторов ă, č и ĕ справедливы равенства:
1. ă + č = č + ă (переместительный закон);
2. ( ă + č )+ ĕ = ă +( č + ĕ ).
Теорема: Для любых векто- Произведение любого вектора на число
ров ă и č справедливо равенство: 0 есть нулевой вектор.
ă – č = ă + ( - č ).
Для любого числа k и любого векто- ( kl )ă= k ( l ă ) (сочетательный закон);
ра ă векторы ă и k ă коллинеарны. ( k + l )ă= k ă+ l ă(1ый рспред-ный закон);
k (ă+č )= k ă+ k č.
Теорема: Средняя линия тра-
Класс.
Глава X .
Метод координат.
Лемма: Если векторы ă и č Теорема: Любой вектор можно раз-
коллинеарны и ă=0, то сущес- ложить по 2ум данным неколлинеар-
твует такое число k , что č= k ă. ным векторам, причём коэффициен-
ты разложения определяются един-
Каждая координата суммы 2ух ственным образом.
векторов = сумме соответству-
ющих координат этих векторов. Каждая координата произведения век-
тора на число = произведению соот-
Каждая координата разности ветствующей координаты вектора
2ух векторов = разности соот- на это число.
ветствующих координат век-
тора на это число. Координаты точки М = соответству-
ющим координатам её радиус-вектора.
Каждая координата вектора =
разности соответствующих ко- Каждая координата середины отрезка
ординат его конца и начала. равна полусумме соответствующих ко-
ординат его концов.
Глава XI .
Соотношения между сторонами
И углами 3-угольника.
Скалярное произведение
Векторов.
Для любого угла α из промежут- tg угла α(α=90°) называется отношение
ка 0° <α<180° sin угла α называ- sin α/ cos α.
ется ордината у точки М, а cos
угла α – абсцисса х угла α. sin (90°-- α)= cos α
Теорема: S 3-угольника = ½ Теорема: Стороны 3-угольника про-
Класс.
Глава I .
Точки, прямые, отрезки.
Через любые две точки Если две прямые имеют общую
можно провести прямую, точку, то они пересекаются.
и притом только одну.
Прямая а и точки А и В.
Прямая а и b пересекаются в точке О.
Две прямые либо имеют только одну общую точку,
либо не имеют общих точек.
Угол.
Угол – это геометрическая фигура, Угол называется развёрнутым, которая состоит из точки и двух лучей, если обе его стороны
исходящих из этой точки. лежат на одной прямой.
Угол с вершиной О и сторонами h и k. Развёрнутый угол с вершиной С
и сторонами p и q.
Развёрнутый угол = 180º; Неразвёрнутый угол < 180º .
Луч, исходящий из вершины угла и Два угла, у которых одна общая
делящий его на два равных угла, сторона общая, а две другие
называется биссектриса угла. являются продолжениями одна
другой, называются смежными.
Два угла, называются вертикальными,
если стороны одного угла являются Сумма смежных углов = 180º.
продолжениями сторон другого.
Две пересекающиеся прямые
Вертикальные углы равны. называются перпендикулярными,
если они образуют 4 прямых угла.
Глава I I.
Треугольники.
Треугольник – геометрическая фигура, Р АВС = АВ+ВС+СА.
кот-ая состоит из 3 точек, не лежа-
щих на 1 прямой, соединённых отрезками.
В равных треугольниках против
Треугольник с вершинами А, В, С и соответственно равных сторон
Сторонами а, b, c. лежат равные углы, также против
соответственно равных равных
углов лежат равные стороны.
Теорема: Если 2 стороны и угол Теорема: Из точки, не лежа-
между ними 1-го треугольника щей на прямой, можно провести
соответственно равны 2 сторонам перпендикуляр к этой, и притом
и углу между ними другого только один.
треугольника, то треугольники равны.
Отрезок, соединяющий вершину треуг- Отрезок бисс-сы угла треуг-ка,
ка с серединой противоположной сто- соединяющий вершину треуг-ка
роны, называется медианой треуг-ка. с точкой противоположной сторо- ны, называется бисс-сой треуг-ка.
Перпендикуляр, проведённый из верши-
ны треуг-ка к прямой, содержащей Треуг-к, у кот-го 2 стороны равны,
противоположную сторону, называ- называется равнобедренным.
ется высотой треуг-ка.
Теорема: В равнобедренном треуг-ке
ВН - высота треуг-ка АВС. углы при основании равны.
Теорема: В равнобедренном Высота равнобедренного треуг-ка, про-
треуг-ке бисс-са, проведённая ведённая к основанию, является медианой
к основа-нию, является и бисс-сой.
Медианой и высотой.
Медиана, проведённая к основанию, явля-
ется высотой и бисс-сой.
Теорема: Если сторона и 2 Теорема: Если три стороны 1го
Дата: 2019-05-29, просмотров: 210.
