Для построения графиков функций со значениями x и у, изменяющимися в широких пределах, нередко используются логарифмические масштабы. Рассмотрим команды, которые используются в таких случаях.

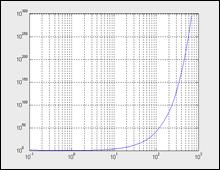
· loglogx(...) - синтаксис команды аналогичен ранее рассмотренному для функции plot(...). Логарифмический масштаб используется для координатных осей X и Y. Ниже дан пример применения данной команды:

>> x=logspace(-1,3);

>> loglog(x,exp(x)./x) grid on

Функция x = logspace(d1, d2) формирует вектор-строку, содержащую 50 равноотстоящих в логарифмическом масштабе точек, которые покрывают диапазон от 10^d1 до 10^d2 .

Функция x =logspace(d1, d2, n) формирует вектор-строку, содержащую n равноотстоящих в логарифмическом масштабе точек, которые покрывают диапазон от 10^d1 до 10^d2.

На рисунке представлен график функции ехр(х)/х в логарифмическом масштабе. Командой grid on строится координатная сетка. Неравномерное расположение линий координатной сетки указывает на логарифмический масштаб осей.

Графики в полулогарифмическом масштабе

В некоторых случаях предпочтителен полулогарифмический масштаб графиков, когда по одной оси задается логарифмический масштаб, а по другой — линейный.

Для построения графиков функций в полулогарифмическом масштабе используются следующие команды: semilogx(...) — строит график функции в логарифмическом масштабе (основание 10) по оси X и линейном по оси Y; semilogy(...)— строит график функции в логарифмическом масштабе по оси Y и линейном по оси X.

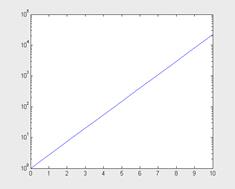
Запись параметров (...) выполняется по аналогии с функцией plot(...). приведем пример построения графика экспоненциальной функции:

>> x=0:0.5:10;

>> semilogy(x,exp(x))

Нетрудно заметить, что при таком масштабе график экспоненциальной функции выродился в прямую линию. Масштабной сетки теперь уже нет.

Столбцовые диаграммы

Столбцовые диаграммы широко используются в литературе, посвященной финансам и экономике, а также в математической литературе. Ниже представлены команды для построения таких диаграмм.

· bar(x, Y) — строит столбцовый график элементов вектора Y (или группы столбцов для матрицы Y) со спецификацией положения столбцов, заданной значениями элементов вектора х, которые должны идти в монотонно возрастающем порядке;

· bar(Y) — строит график значений элементов матрицы Y так же, как указано выше, но фактически для построения графика используется вектор х=1:m;

· bar(x,Y,WIDTH) или bar(Y,WIDTH) — команда аналогична ранее рассмотренным, но со спецификацией ширины столбцов (при WIDTH > 1 столбцы в одной и той же позиции перекрываются). По умолчанию задано WIDTH = 0.8.

Возможно применение этих команд и в следующем виде: bar(.... 'Спецификация') для задания спецификации графиков, например типа линий, цвета и т. д., по аналогии с командой plot. Спецификация 'stacked' задает рисование всех n столбцов в позиции m друг на друге.

Пример построения столбцовой диаграммы матрицы размером 12x3 приводится ниже:

>> %Столбцовая диаграмма

>> subplot(2,1,1), bar(rand(12,3),stacked'), colormap(cool)

Помимо команды bar(...) существует аналогичная ей по синтаксису команда barh(...), которая" строит столбцовые диаграммы с горизонтальным расположением столбцов.

>> subplot(2,1,1), barh(rand(5,3), 'stacked'),colormap(cool)

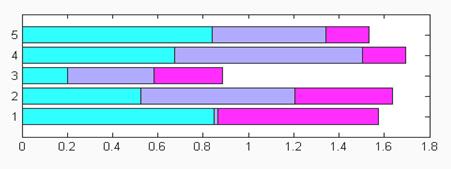
Какое именно расположение столбцов выбрать, зависит от пользователя, использующего эти команды для представления своих данных.

Построение гистограмм

Классическая гистограмма характеризует числа попаданий значений элементов вектора Y в М интервалов с представлением этих чисел в виде столбцовой диаграммы. Для получения данных для гистограммы служит функция hist, записываемая в следующем виде:

· N=hist(Y) — возвращает вектор чисел попаданий для 10 интервалов, выбираемых автоматически. Если Y — матрица, то выдается массив данных о числе попаданий для каждого из ее столбцов;

· N=hist(Y,M) — аналогична вышерассмотренной, но используется М интервалов (М- скаляр);

· N=hist(Y,X) — возвращает числа попаданий элементов вектора Y в интервалы, центры которых заданы элементами вектора X;

· [N,X]=HIST(...) — возвращает числа попаданий в интервалы и данные о центрах интервалов.

Команда hist(...) с синтаксисом, аналогичным приведенному выше, строит график гистограммы. В следующем примере строится гистограмма для 1000 случайных чисел и выводится вектор с данными о числах их попаданий в интервалы, заданные вектором x:

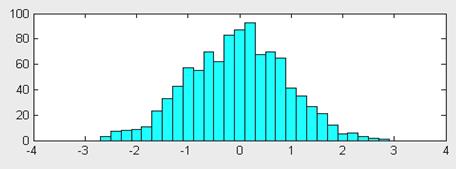
>> x=-3:0.2:3;

>> y=randn(1000,1);

>> hist(y,x)

>> h=hist(y,x)

h =

Columns 1 through 9

0 0 3 7 8 9 11 23 33

Columns 10 through 18

43 57 55 70 62 83 87 93 68

Columns 19 through 27

70 65 41 35 27 21 12 5 6

Columns 28 through 31

3 2 1 0

Нетрудно заметить, что распределение случайных чисел близко к нормальному закону. Увеличив их количество, можно наблюдать еще большее соответствие этому закону.