Основы графической визуализации вычислений
Особенности графики системы MATLAB
· Построение графика функций одной переменной
· Построение графиков точками и отрезками прямых
· Графики в логарифмическом и полулогарифмическом масштабе
· Гистограммы и диаграммы
· Графики специальных типов
· Создание массивов данных для трехмерной графики
· Построение графиков трехмерных поверхностей, сечений и контуров
· Средства управления подсветкой и обзором фигур
· Средства оформления графиков
· Одновременный вывод нескольких графиков
· Управление цветовой палитрой
· Окраска трехмерных поверхностей
· Двумерные и трехмерные графические объекты
Основные отличительные черты графики MATLAB
· существенно улучшенный интерфейс графических окон;
· введение новой панели инструментов Camera для интерактивного изменения условий видимости объекта;
· расширенные возможности форматирования графики;
· возможность создания графики в отдельных окнах;
· возможность вывода нескольких графических окон;
· возможность перемещения окон по экрану и изменения их размеров;
· возможность перемещения области графики внутри графического окна;
· задание различных координатных систем и осей;
· высокое качество графики;
· широкие возможности использования цвета;
· легкость установки графических признаков - атрибутов;
· снятие ограничений на число цветов;
· обилие параметров команд графики;
· возможность получения естественно выглядящих трехмерных фигур и их сочетаний;
· простота построения трехмерных графиков с их проекцией на плоскость;
· возможность построения сечений трехмерных фигур и поверхностей плоскостями;
· функциональная многоцветная и полутоновая окраска;
· возможность имитации световых эффектов при освещении фигур точечным источником света;
· возможность создания анимационной графики;
· возможность создания объектов для типового интерфейса пользователя.
Построение графика функций одной переменной
В режиме непосредственных вычислений доступны практически все возможности системы. Широко используется построение графиков различных функций, дающих наглядное представление об их поведении в широком диапазоне изменения аргумента. При этом графики строятся в отдельных масштабируемых и перемещаемых окнах.
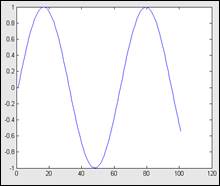
Рассмотрим простейший пример - построение графика синусоиды. MATLAB строит графики функций по ряду точек, соединяя их отрезками прямых, т. е. осуществляя линейную интерполяцию функции в интервале между смежными точками. Зададим интервал изменения аргумента x от 0 до 10 с шагом 0.1. Для построения графика достаточно вначале задать вектор х=0:0.1:10, а затем использовать команду построения графиков plot (sin(x)).
Вектор x задает интервал изменения независимой переменной от 0 до 10 с шагом 0.1. Функция plot строит не истинный график функции sin(x), а лишь заданное числом элементов вектора x число точек. Эти точки затем просто соединяются отрезками прямых, т. е. осуществляется кусочно-линейная интерполяция данных графика. При 100 точках полученная кривая глазом воспринимается как вполне плавная, но при 10 - 20 точках она будет выглядеть состоящей из отрезков прямых.
MATLAB строит графики в отдельных окнах, называемых графическими окнами. В главном меню окна команды пункта меню Tools (Инструменты), позволяют вывести или скрыть инструментальную панель. Средства этой панели позволяют легко управлять параметрами графиков и наносить на них текстовые комментарии в любом месте.
Графическая функция fplot
MATLAB имеет средства для построения графиков и таких функций, как sin(x)/x, которые имеют устранимые неопределенности. Это делается, с помощью другой графической команды –
fplot: fplot('f(x)', [xmin, xmax])
Она позволяет строить функцию, заданную в символьном виде, в интервале изменения аргумента х от xmin до xmax без фиксированного шага изменения х. Хотя в процессе вычислений предупреждение об ошибке (деление на 0) выводится, график строится правильно, при х=0 sinx/x=1. Команда grid on (сетка)- включает отображение сетки, которая строится пунктирными линиями.
>> fplot('sin(x)/x', [-15,15]); grid on
Столбцовые диаграммы
Столбцовые диаграммы широко используются в литературе, посвященной финансам и экономике, а также в математической литературе. Ниже представлены команды для построения таких диаграмм.
· bar(x, Y) — строит столбцовый график элементов вектора Y (или группы столбцов для матрицы Y) со спецификацией положения столбцов, заданной значениями элементов вектора х, которые должны идти в монотонно возрастающем порядке;
· bar(Y) — строит график значений элементов матрицы Y так же, как указано выше, но фактически для построения графика используется вектор х=1:m;
· bar(x,Y,WIDTH) или bar(Y,WIDTH) — команда аналогична ранее рассмотренным, но со спецификацией ширины столбцов (при WIDTH > 1 столбцы в одной и той же позиции перекрываются). По умолчанию задано WIDTH = 0.8.
Возможно применение этих команд и в следующем виде: bar(.... 'Спецификация') для задания спецификации графиков, например типа линий, цвета и т. д., по аналогии с командой plot. Спецификация 'stacked' задает рисование всех n столбцов в позиции m друг на друге.
Пример построения столбцовой диаграммы матрицы размером 12x3 приводится ниже:
>> %Столбцовая диаграмма
>> subplot(2,1,1), bar(rand(12,3),stacked'), colormap(cool)

Помимо команды bar(...) существует аналогичная ей по синтаксису команда barh(...), которая" строит столбцовые диаграммы с горизонтальным расположением столбцов.
>> subplot(2,1,1), barh(rand(5,3), 'stacked'),colormap(cool)
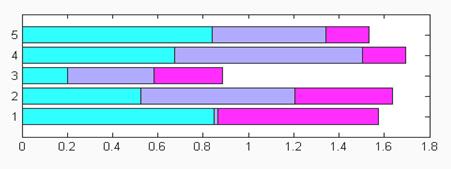
Какое именно расположение столбцов выбрать, зависит от пользователя, использующего эти команды для представления своих данных.
Построение гистограмм
Классическая гистограмма характеризует числа попаданий значений элементов вектора Y в М интервалов с представлением этих чисел в виде столбцовой диаграммы. Для получения данных для гистограммы служит функция hist, записываемая в следующем виде:
· N=hist(Y) — возвращает вектор чисел попаданий для 10 интервалов, выбираемых автоматически. Если Y — матрица, то выдается массив данных о числе попаданий для каждого из ее столбцов;
· N=hist(Y,M) — аналогична вышерассмотренной, но используется М интервалов (М- скаляр);
· N=hist(Y,X) — возвращает числа попаданий элементов вектора Y в интервалы, центры которых заданы элементами вектора X;
· [N,X]=HIST(...) — возвращает числа попаданий в интервалы и данные о центрах интервалов.
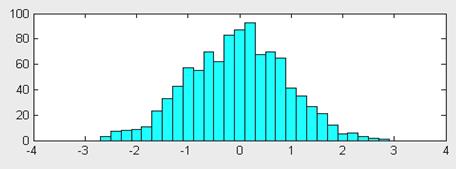
Команда hist(...) с синтаксисом, аналогичным приведенному выше, строит график гистограммы. В следующем примере строится гистограмма для 1000 случайных чисел и выводится вектор с данными о числах их попаданий в интервалы, заданные вектором x:
>> x=-3:0.2:3;
>> y=randn(1000,1);
>> hist(y,x)
>> h=hist(y,x)
h =
Columns 1 through 9
0 0 3 7 8 9 11 23 33
Columns 10 through 18
43 57 55 70 62 83 87 93 68
Columns 19 through 27
70 65 41 35 27 21 12 5 6
Columns 28 through 31
3 2 1 0
Нетрудно заметить, что распределение случайных чисел близко к нормальному закону. Увеличив их количество, можно наблюдать еще большее соответствие этому закону.
Установка титульной надписи
После того как график уже построен, MATLAB позволяет выполнить его форматирование или оформление в нужном виде. Соответствующие этому средства описаны ниже. Так, для установки над графиком титульной надписи используется следующая команда:
· title( 'string') — установка на двумерных и трехмерных графиках титульной надписи, заданной строковой константой 'string'.
Установка осевых надписей
Для установки надписей возле осей х, у и z используются следующие команды:
xlabel('String')
ylabel ('String')
zlabell ('String')
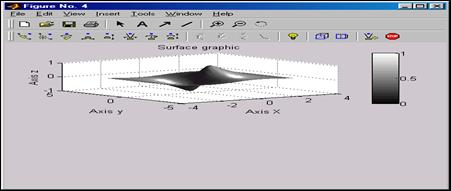
Соответствующая надпись задается символьной константой или переменной 'String'. Пример установки титульной надписи и надписей по осям графиков приводится ниже:
>> surfl(X,Y,Z)
>> [X,Y]=meshgrid(-3:0.15:3);
>> Z=sin(X)./(X.^2+Y.^2+0.3);
>> surfl(X,Y,Z)
>> colorbar
>> colormap(gray)
>> shading interp
>> xlabel('Axis X')
>> ylabel('Axis Y')
>> zlabel('Axis Z')
>> title('Surface graphic')
Разбиение графического окна
Бывает, что в одном окне надо расположить несколько координатных осей с различными графиками без наложения их друг на друга. Для этого используются команды subplot, применяемые перед построением графиков:
· subplot — создает новые объекты класса axes (подокна);
· subplot(m,n, p) или subplot(mnp) — разбивает графическое окно на тхп подокон, при этом m — число подокон по горизонтали, n — число подокон по вертикали, а p— номер подокна, в которое будет выводиться текущий график (подокна отсчитываются последовательно по строкам);
· subplot(H), где Н — дескриптор для объекта axes, дает альтернативный способ задания подокна для текущего графика;
· subplot( 'position',[left bottom width height]) — создает подокно с заданными нормализованными координатами (в пределах от 0.0 до 1.0);
· subplot(lll) и clf reset — удаляют все подокна и возвращают графическое окно в обычное состояние.
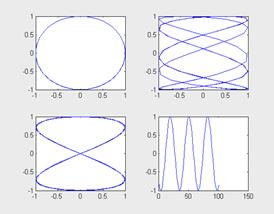
Следующий пример иллюстрирует применение команды subplot:
>> x=-5:0.1:5;
>> subplot(2,2,1), plot(sin(x), cos(x))
>> subplot(2,2,2), plot(sin(5*x), cos(2*x+0.2))
>> subplot(2,2,3), plot(sin(4*x), cos(2*x))
>> subplot(2,2,4), plot(cos(2*x))
В этом примере последовательно строятся четыре графика различного типа, размещаемых в разных подокнах.
Для всех графиков возможна индивидуальная установка дополнительных объектов, например титульных надписей, надписей по осям и т. д.
Изменение масштаба графика
Для изменения масштаба двумерных графиков используются команды класса zoom:
· zoom — переключает состояние режима интерактивного изменения масштаба для текущего графика;
· zoom (FACTOR) устанавливает масштаб в соответствии с коэффициентом FACTOR;
· zoom on — включает режим интерактивного изменения масштаба для текущего графика;
· zoom off — выключает режим интерактивного изменения масштаба для текущего графика;
· zoom out — обеспечивает полный просмотр, т. е. устанавливает стандартный масштаб графика;
· zoom xon или zoom yon — включает режим изменения масштаба только по оси x или по оси у;
· zoom reset — запоминает текущий масштаб в качестве масштаба по умолчанию для данного графика;

Команда zoom позволяет управлять масштабированием графика с помощью мыши. Для этого надо подвести курсор мыши к интересующей вас области рисунка. Если команда zoom включена (on), то нажатие левой кнопки увеличивает масштаб вдвое, а правой — уменьшает вдвое. При нажатой левой кнопке мыши можно выделить пунктирным черным прямоугольником нужный участок графика — при отпускании кнопки он появится в увеличенном виде и в том масштабе, который соответствует выделяющему прямоугольнику.
Рассмотрим работу команды zoom на следующем примере:
>> x=-5:0.1:5;
>> plot(x, sin(x.^5)./(x.^5+eps))
>> zoom on
После прекращения манипуляций левой кнопкой мыши график примет вид, показанный на рисунке. Теперь в полный размер графического окна будет развернуто изображение, попавшее в выделяющий прямоугольник.

Команда zoom, таким образом, выполняет функцию «лупы», позволяющей наблюдать в увеличенном виде отдельные фрагменты сложных графиков. Однако следует учитывать, что для наблюдения фрагментов графиков при высоком увеличении они должны быть заданы большим количеством точек. Иначе вид отдельных фрагментов и тем более особых точек (в нашем случае это точка при x вблизи нуля) будет существенно отличаться от истинного.
Установка палитры цветов
Поскольку графика MATLAB обеспечивает получение цветных изображений, в ней есть ряд команд для управления цветом и различными световыми эффектами. Среди них важное место занимает установка палитры цветов. Палитра цветов RGB задается матрицей MAP из трех столбцов, определяющих значения интенсивности красного (red), зеленого (green) и синего (blue) цветов. Их интенсивность задается в относительных единицах от 0.0 до 1.0. Например, [0 0 0] задает черный цвет, [1 1 1] — белый цвет, [0 0 1] — синий цвет. При изменении интенсивности цветов в указанных пределах возможно задание любого цвета. Таким образом, цвет соответствует общепринятому формату RGB.
Для установки палитры цветов служит команда colormap, записываемая в следующих формах:
· colormap( 'default') — устанавливает палитру по умолчанию, при которой распределение цветов соответствует радуге;
· colormap(MAP) — устанавливает палитру RGB, заданную матрицей MAP;
· C= colormap — функция возвращает матрицу текущей палитры цветов С.
m-файл с именем colormap устанавливает свойства цветов для текущего графика.
Команда help graph3d наряду с прочим выводит полный список характерных палитр, используемых графической системой MATLAB:
· hsv - цвета радуги;
· hot - чередование черного, красного, желтого и белого цветов;
· gray - линейная палитра в оттенках серого цвета;
· bone - серые цвета с оттенком синего;
· copper - линейная палитра с оттенками меди;
· pink - розовые цвета с оттенками пастели;
· white - палитра белого цвета;
· flag - чередование красного, белого, синего и черного цветов;
· lines - палитра с чередованием цветов линий;
· colorcube - расширенная палитра RGB;
· jet - разновидность палитры HSV;
· prism - призматическая палитра цветов;
· cool - оттенки голубого и фиолетового цветов;
· autumn -оттенки красного и желтого цветов;
· spring - оттенки желтого и фиолетового цветов;
· winter - оттенки синего и зеленого цветов;
· summer - оттенки зеленого и желтого цветов.
Все эти палитры могут служить параметрами команды colormap, например colormap(hsv) фактически устанавливает то же, что и команда colormap( 'default').
Построение сферы
Для расчета массивов X, Y и Z координат точек сферы как трехмерной фигуры используется функция sphere:
· [X,Y,Z]=sphere(N) — генерирует матрицы X, Y и Z размера (N+1)x (N+1) для последующего построения сферы с помощью команд surfl (X, Y,Z) или surfl(X,Y,,Z);
· [X,Y,Z]=sphere — аналогична предшествующей функции при N=20.

Пример применения этой функции:
>> [X,Y,Z]=sphere(30);
>> surfl(X,Y,Z)
Хорошо видны геометрические искажения (сфера приплюснута), связанные с разными масштабами по координатным осям.
Обратите внимание на то, что именно функциональная окраска сферы придает ей довольно реалистичный вид. В данном случае цвет задается вектором Z.
Основы графической визуализации вычислений
Дата: 2019-05-29, просмотров: 386.