Эти функции обычно интегрируют путём замены переменной, которая сводит интеграл от иррациональной функции к интегралу от рациональной функции относительно новой переменной.

I. 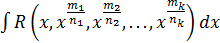, где , .

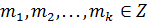Символ 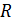 означает, что над величинами, перечисленными в скобках, выполняются рациональные действия: сложение, вычитание, умножение, деление и возведение в степень с целым показателем. Для вычисления интеграла от иррациональной функции вида I необходимо выполнить замену 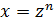, где 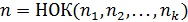. Относительно  подынтегральное выражение будет рациональной функцией. 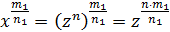, показатель степени – целое число. Аналогично показывается, что каждая иррациональность в интеграле I превращается в рациональную функцию относительно . 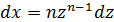, т.е  тоже рационально выражается через .

Интеграл I принимает вид .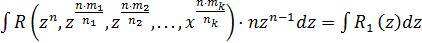

Пример.

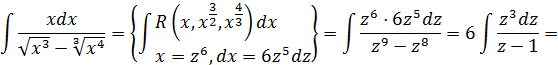
II. , где , , .

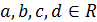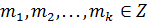Для вычисления интеграла от иррациональной функции вида II, нужно выполнить замену 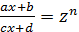, где .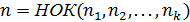

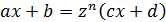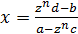По аналогии с интегралом типа I доказывается, что все иррациональные выражения в II выражаются через  как рациональные. Покажем, что  тоже рационально выражается через . Из формулы замены , . Т.к. производная от дробно-рациональной функции является тоже дробно-рациональной функцией, то  будет рационально выражаться через . Значит, интеграл будет вида .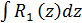

Частным случаем интеграла II будет  при

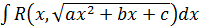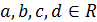III. , где . Для вычисления интеграла такого вида применяют подстановки Эйлера:

1) если 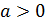, то ,

2) если , то 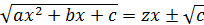, знак можно выбирать любой

3) если многочлен 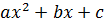 имеет различные действительные корни 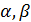, то 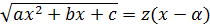,  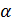- любой корень.

Можно показать, что в каждом из этих случаев интеграл сводится к интегралу от рациональной функции относительно .

Пример.

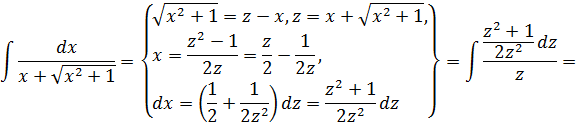
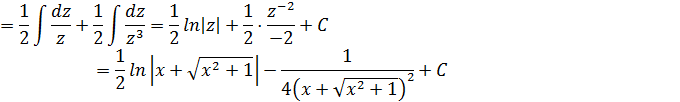
Частные случаи интеграла III

1. 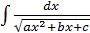 и .

Для вычисления интегралов под корнем выделяют полный квадрат и сводят к табличным интегралам 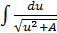 или  - для первого;  или 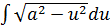 - для второго.

2. 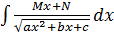 и , .

При вычислении интегралов этого типа применяется алгоритм, аналогичный алгоритму вычисления интеграла от простейшей дроби третьего типа, т.е. на месте 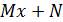 создают производную подкоренного выражения  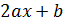и разбивают на сумму двух интегралов.

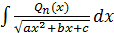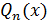3. , где  – многочлен степени .

При вычислении интеграла используется рекуррентная формула

, (*)

где  – многочлен степени на 1 меньше с неизвестными коэффициентами, – неизвестная постоянная.

Для нахождения неизвестных коэффициентов  необходимо:

1. продифференцировать равенство (*) по , используя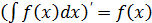

,

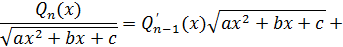
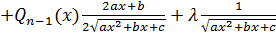2. умножить полученное равенство на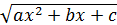

.

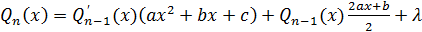Пришли к равенству двух многочленов: слева известный многочлен, справа – с неизвестными коэффициентами

3. приравнять коэффициенты при одинаковых степенях полученных многочленов. Приходим к системе  уравнений с  неизвестными, откуда найти коэффициенты.

Найденные коэффициенты подставить в равенство (*) и вычислить интеграл.

4. , где , , .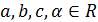

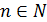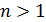При вычислении интеграла используется замена

, , .

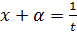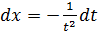В результате интеграл приводится к виду 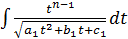, т.е к виду 3.

Интеграл от биномиального дифференциала

Биноминальным дифференциалом называется выражение вида 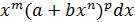, где ; .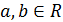

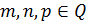Русский математик Чебышёв П.Л. показал, что интеграл от биноминального дифференциала сводится к интегралу от рациональной функции относительно новой переменной только в трёх случаях:

1) , при этом 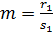, ; тогда это интеграл типа I; выполняется замена 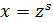, где 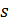– наименьшее общее кратное среди знаменателей дробей и .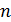

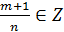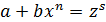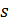2) , ; тогда применяют подстановку , где – знаменатель дроби . Можно показать, что при этой замене интеграл приводится к интегралу от рациональной функции.

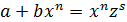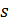3) , ; тогда подстановка имеет вид , где – знаменатель дроби .

О. Если неопределённый интеграл функции  выражается через элементарные функции с помощью конечного числа элементарных операций (сложение, вычитание, умножение, деление, возведение в степень) и конечного числа суперпозиции этих функций (взятия функции от функции), то говорят, что неопределённый интеграл функции  выражается в конечном виде через элементарные функции, или говорят «интеграл берётся в конечном виде».

К числу интегралов, не берущихся в конечном виде относятся:

, , , , , ;

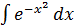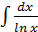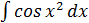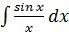эллиптические интегралы

, .

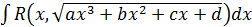Интегрирование приводит к появлению новых функций.