ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Первообразная и неопределённый интеграл
Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции. Интегральное исчисление решает обратную задачу – нахождение самой функции по её производной или дифференциалу.
О. Функция  называется первообразной для функции
называется первообразной для функции  на интервале
на интервале  , если в каждой точке этого интервала
, если в каждой точке этого интервала 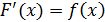 , т.е. это такая функция, производная которой равна
, т.е. это такая функция, производная которой равна  . Например,
. Например, 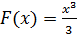 - первообразная для функции
- первообразная для функции 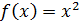 .
.
Свойства первообразных:
1. Если  – первообразная для функции
– первообразная для функции  на интервале
на интервале  , то и функция
, то и функция 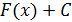 является первообразной для функции
является первообразной для функции  на интервале
на интервале  при любом постоянном С.
при любом постоянном С.
Доказательство. Из условия теоремы следует, что 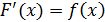
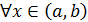 . Тогда
. Тогда 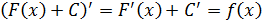 , следовательно,
, следовательно, 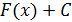 - первообразная для функции
- первообразная для функции  на интервале (a, b) при любом постоянном С.
на интервале (a, b) при любом постоянном С.
2. Если функции  и
и 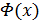 являются первообразными для функции
являются первообразными для функции  на интервале
на интервале  , то их разность
, то их разность 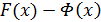 постоянна.
постоянна.
Доказательство. Из условия теоремы следует, что 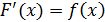 ,
, 
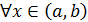 . Тогда
. Тогда 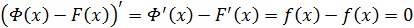 , следовательно,
, следовательно, 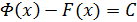 по достаточному условию постоянства функции.
по достаточному условию постоянства функции.
Из этих свойств следует, что если функция  имеет хотя бы одну первообразную
имеет хотя бы одну первообразную  в интервале
в интервале  , то она имеет бесчисленное множество первообразных, и все они содержатся в формуле
, то она имеет бесчисленное множество первообразных, и все они содержатся в формуле 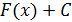 , где С – любое постоянное.
, где С – любое постоянное.
О. Неопределённым интегралом функции  в интервале
в интервале  называется множество всех её первообразных на этом интервале.
называется множество всех её первообразных на этом интервале.
Обозначение: 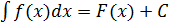 .
.
 – подынтегральная функция,
– подынтегральная функция,  – подынтегральное выражение.
– подынтегральное выражение.
Таблица интегралов элементарных функций
1. 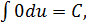
| 2. 
|
3. 
| 4. 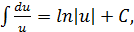
|
5. 
| 6. 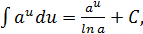
|
7. 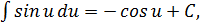
| 8. 
|
9. 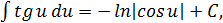
| 10. 
|
11. 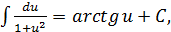
| 12. 
|
13. 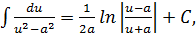
| 14. 
|
15. 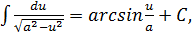
| 16. 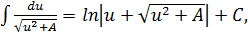
|
17. 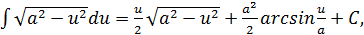
18. 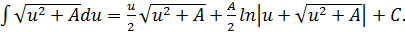
19. 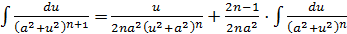
Методы интегрирования
1. Непосредственное интегрирование – подынтегральную функцию преобразовывают так, чтобы возникли табличные интегралы. Пример: 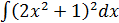 .
.
2. Метод замены переменной (метод подстановки).
Теорема. Если функция  непрерывна на
непрерывна на  , а функция
, а функция 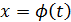 непрерывна вместе со своей производной на
непрерывна вместе со своей производной на  , причём
, причём 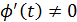
 , и если функция
, и если функция 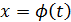 отображает
отображает  на
на  , то имеет место формула
, то имеет место формула
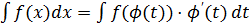 . (1)
. (1)
В интеграле справа мыслится  , зависящее от
, зависящее от  , т.е.
, т.е.  , где
, где  - функция, обратная функции
- функция, обратная функции 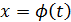 .
.
Доказательство.
1. Докажем, что функция 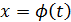 имеет обратную. Т.к.
имеет обратную. Т.к. 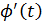 непрерывна на
непрерывна на  , и
, и 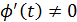 , то по свойству непрерывной функции
, то по свойству непрерывной функции 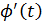 сохраняет постоянный знак на
сохраняет постоянный знак на  (доказывается методом от противного). Т.е либо
(доказывается методом от противного). Т.е либо 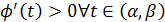 , либо
, либо 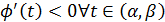 , а тогда функция
, а тогда функция 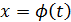 либо строго возрастает на
либо строго возрастает на  , либо строго убывает на
, либо строго убывает на  . Из непрерывности
. Из непрерывности 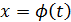 и её монотонности на
и её монотонности на  следует, что на
следует, что на  для функции
для функции 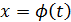 существует обратная функция
существует обратная функция  ,
, 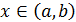 . По теореме о производной обратной функции получаем, что
. По теореме о производной обратной функции получаем, что
 . (2)
. (2)
2. Докажем равенство (1). Докажем, что существует каждый интеграл в равенстве (1). Ссылаясь на теорему об интегрируемости (если функция непрерывна на  , то она интегрируема на нём).
, то она интегрируема на нём).
 непрерывна на
непрерывна на  по условию, следовательно, существует
по условию, следовательно, существует 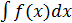 . Рассмотрим функцию под интегралом справа.
. Рассмотрим функцию под интегралом справа.
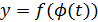 - сложная функция, разобьём её на цепочку более простых:
- сложная функция, разобьём её на цепочку более простых:
1) 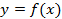 непрерывна на
непрерывна на  ;
;
2) 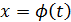 непрерывна на
непрерывна на  по условию
по условию
3) функция 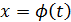 отображает
отображает  на
на  .
.
Выполняются все 3 условия о непрерывности сложной функции. Тогда сложная функция 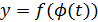 непрерывна на
непрерывна на  .
.
Функция 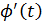 непрерывна на
непрерывна на  по условию. Тогда функция
по условию. Тогда функция  непрерывна на
непрерывна на  по теореме о непрерывности произведения, следовательно, интеграл в равенстве справа существует.
по теореме о непрерывности произведения, следовательно, интеграл в равенстве справа существует.
Чтобы доказать равенство (1) достаточно показать, что правая часть при  даёт множество первообразных для функции
даёт множество первообразных для функции  , которая является подынтегральной функцией слева, а для этого достаточно показать, что производная правой части по переменной
, которая является подынтегральной функцией слева, а для этого достаточно показать, что производная правой части по переменной  равна
равна  .
.
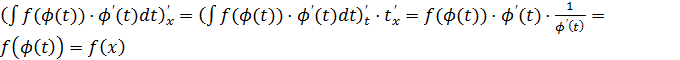 .
.
Примеры применения этого метода – вывод формул 15 и 12 таблицы.
 .
.
Самостоятельно с помощью той же замены 12.
Замечание. Иногда формулу замены применяют справа налево, а именно, если интеграл имеет вид 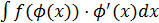 , то делают замену
, то делают замену  ,
, 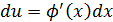 , интеграл принимает вид
, интеграл принимает вид 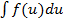 .
.
Примеры: 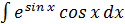 ,
, 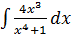
3. Метод интегрирования по частям
Теорема. Если функции 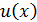 и
и 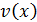 дифференцируемы в интервале
дифференцируемы в интервале  , то имеет место формула интегрирования по частям
, то имеет место формула интегрирования по частям  , при условии, что оба интеграла существуют.
, при условии, что оба интеграла существуют.
Доказательство.
Из дифференцируемости функций 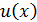 и
и 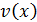 в
в  следует, что их произведение тоже дифференцируемо в
следует, что их произведение тоже дифференцируемо в  . По формуле дифференциала произведения
. По формуле дифференциала произведения
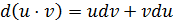 . (1)
. (1)
Отсюда
 . (2)
. (2)
Проинтегрируем это равенство. Из (1) видно, что правая часть интегрируема в  . Тогда интеграл в левой части (1) существует по свойству (3) интегралов.
. Тогда интеграл в левой части (1) существует по свойству (3) интегралов.
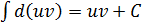 . В результате из (2) получаем
. В результате из (2) получаем
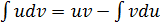 .
.
При этом 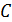 не пишем.
не пишем.
Замечание. Выбор 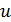 и
и 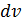 диктуется тем, чтобы новый интеграл
диктуется тем, чтобы новый интеграл  был проще исходного.
был проще исходного.
Рекомендации по выбору 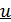 и
и  , когда интеграл имеет вид
, когда интеграл имеет вид 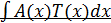 , где
, где 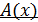 - алгебраическая функция,
- алгебраическая функция, 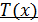 – трансцендентная:
– трансцендентная:
1. Если  , то
, то 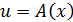 ,
, 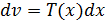 .
.
2. Если  , то,
, то, 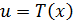 ,
, 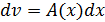 .
.
Примеры. 1.  . 2.
. 2. 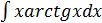 .
.
Вывод формул 17 и 18 таблицы.
17. 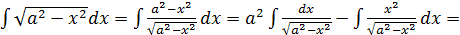
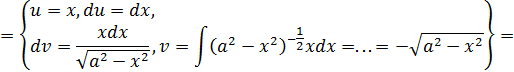
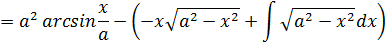
Выпишем начало и конец формулы
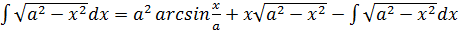 ,
,
 ,
,
 .
.
18. 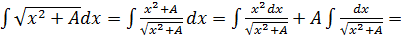
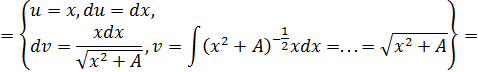
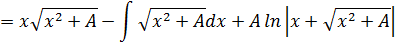
 ,
,
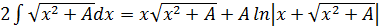 ,
,
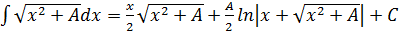 .
.
Вывод рекуррентной формулы 19. Обозначим  ,
,
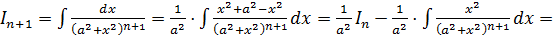
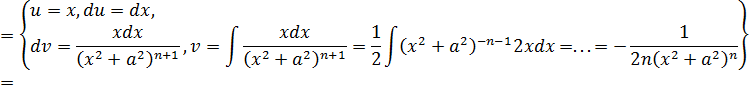


 -
-
Это рекуррентная формула, сводящая вычисление интеграла с показателем степени  к интегралу такого же вида степени
к интегралу такого же вида степени 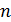 . Формулу применяют, пока не придут к табличному интегралу.
. Формулу применяют, пока не придут к табличному интегралу.
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Первообразная и неопределённый интеграл
Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции. Интегральное исчисление решает обратную задачу – нахождение самой функции по её производной или дифференциалу.
О. Функция  называется первообразной для функции
называется первообразной для функции  на интервале
на интервале  , если в каждой точке этого интервала
, если в каждой точке этого интервала 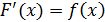 , т.е. это такая функция, производная которой равна
, т.е. это такая функция, производная которой равна  . Например,
. Например, 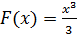 - первообразная для функции
- первообразная для функции 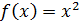 .
.
Свойства первообразных:
1. Если  – первообразная для функции
– первообразная для функции  на интервале
на интервале  , то и функция
, то и функция 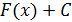 является первообразной для функции
является первообразной для функции  на интервале
на интервале  при любом постоянном С.
при любом постоянном С.
Доказательство. Из условия теоремы следует, что 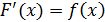
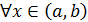 . Тогда
. Тогда 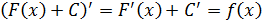 , следовательно,
, следовательно, 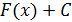 - первообразная для функции
- первообразная для функции  на интервале (a, b) при любом постоянном С.
на интервале (a, b) при любом постоянном С.
2. Если функции  и
и 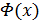 являются первообразными для функции
являются первообразными для функции  на интервале
на интервале  , то их разность
, то их разность 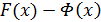 постоянна.
постоянна.
Доказательство. Из условия теоремы следует, что 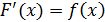 ,
, 
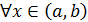 . Тогда
. Тогда 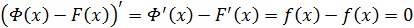 , следовательно,
, следовательно, 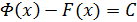 по достаточному условию постоянства функции.
по достаточному условию постоянства функции.
Из этих свойств следует, что если функция  имеет хотя бы одну первообразную
имеет хотя бы одну первообразную  в интервале
в интервале  , то она имеет бесчисленное множество первообразных, и все они содержатся в формуле
, то она имеет бесчисленное множество первообразных, и все они содержатся в формуле 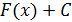 , где С – любое постоянное.
, где С – любое постоянное.
О. Неопределённым интегралом функции  в интервале
в интервале  называется множество всех её первообразных на этом интервале.
называется множество всех её первообразных на этом интервале.
Обозначение: 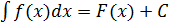 .
.
 – подынтегральная функция,
– подынтегральная функция,  – подынтегральное выражение.
– подынтегральное выражение.
Дата: 2019-05-28, просмотров: 266.