Главные эффекты первого, второго и третьего факторов вычисляются по следующим формулам:
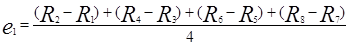 ,
,
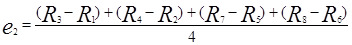 , (5.2)
, (5.2)
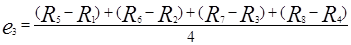 ,
,
где 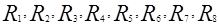 – отклики системы.
– отклики системы.
Эффекты взаимодействия первого и второго, первого и третьего, второго и третьего, первого и второго и третьего факторов вычисляются по следующим формулам:
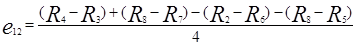 ,
,
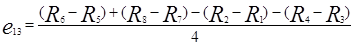 , (5.3)
, (5.3)
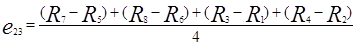 ,
,
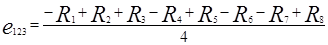 ,
,
где 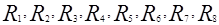 – отклики системы.
– отклики системы.
Значения эффектов для каждого выходного параметра представлены в таблице 5.4.
Таблица 5.4 – Значения эффектов
| Параметр | e1 | e2 | e3 | e12 | e13 | e23 | e123 |
| p | -0,3192115 | -0,0686965 | 0,06653 | -0,6994355 | -0,642834 | -0,0686965 | 0,062186 |
| d | -18,315773 | -3,1235475 | 3,5655875 | -25,774998 | -25,052413 | -3,1235475 | 0,4575825 |
| w | -18,15955 | -3,30525 | 4,48465 | -34,1838 | -32,7314 | -3,30525 | 0,5327 |
| Q | -1,5063818 | -0,424687 | 0,3191838 | -1,7749518 | -1,7066363 | -0,4246868 | 0,10430775 |
| L | -1,1264325 | -0,556723 | 0,4529075 | -2,6504325 | -2,4088725 | -0,5567225 | 0,1591375 |
Общий вид уравнения регрессии представлен ниже:
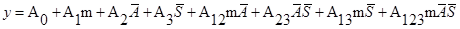 , (5.4)
, (5.4)
где 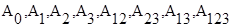 - коэффициенты уравнения регрессии.
- коэффициенты уравнения регрессии.
Значения коэффициентов уравнения регрессии представлены в таблице 5.5. Пример вычисления коэффициентов представлен в приложении Б.
Значения коэффициентов уравнения регрессии представлены в таблице 5.5.
Таблица 5.5 – Значения коэффициентов уравнения регрессии
| Ρ | d | W | Q | L |
| -43,2915 | -235,808 | -45,0088 | -59,9977 | -85,6907 |
| 24,04419 | 144,1403 | 66,1593 | 36,02849 | 57,9095 |
| 3,770473 | 15,9089 | 0,5527 | 4,668797 | 6,93938 |
| 5,335393 | 47,84272 | 27,3329 | 9,391359 | 12,49551 |
| -2,09804 | -10,2775 | -4,1604 | -2,86784 | -4,8038 |
| -0,45454 | -3,17093 | -1,445 | -0,71899 | -0,98899 |
| -2,88832 | -26,2564 | -17,3224 | -5,33401 | -7,76647 |
| 0,248744 | 1,83033 | 1,1306 | 0,417231 | 0,63655 |
Уравнения регрессии для каждого из откликов:
ρ = - 43.2915 + 24.04419m + 3.770473 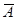 + 5.335393
+ 5.335393 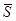 - 2.09804
- 2.09804 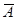 - 0.45454
- 0.45454 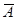
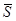 - 2.88832m
- 2.88832m 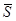 + 0.248744m
+ 0.248744m 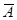
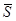 ;
;
d = - 235.808 + 144.1403m + 15.9089 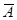 + 47.84272
+ 47.84272 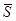 - 10,2775m
- 10,2775m 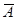 - 3.17093
- 3.17093 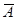
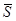 - 26.2564m
- 26.2564m 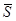 + 1.83033m
+ 1.83033m 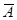
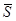 ;
;
w = - 45.0088+ 66.1593m + 0.5527 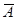 + 273329
+ 273329 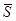 - 4.1604m
- 4.1604m 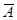 - 1.445
- 1.445 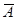
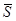 - 17.3224m
- 17.3224m 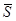 + 1.1306m
+ 1.1306m 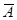
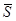 ;
;
Q= - 59.9977 + 36.02849m + 4.668797 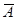 + 9.391359
+ 9.391359 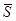 - 2.86784m
- 2.86784m 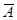 - 0.71899
- 0.71899 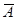
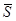 - 5.33401m
- 5.33401m 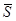 + 0.417231m
+ 0.417231m 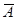
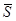 ;
;
l = -85.6907 + 57.9095m + 6.93938 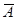 + 12.49551
+ 12.49551 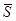 - 4.8038m
- 4.8038m 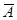 - 0.98889
- 0.98889 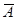
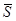 - 7.76647m
- 7.76647m 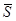 + 0.63655m
+ 0.63655m 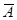
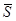 .
.
По уравнениям регрессии для значения для входных параметров m=2, 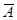 =10,
=10, 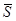 =10 получаем:
=10 получаем:
ρ = 0.4231; d =8.2874; w = 18.1298; Q = 0.1710; l =1.4828.
Для проверки адекватности уравнений регрессии используем метод малых приращений. Так, для значений m, 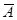 ,
, 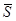 значения были получены выше. В таблице 5.6 представлены результаты при малом приращении с (dm = 0,04),
значения были получены выше. В таблице 5.6 представлены результаты при малом приращении с (dm = 0,04), 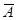 (d
(d 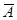 = 0,2),
= 0,2), 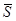 (d
(d 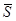 =0,2):
=0,2):
Таблица 5.6 – Метод малых приращений
| N | Dm | d | d | Ρ | d | w | Q | L |
| 1 | 0 | 0 | 0 | 0.4231 | 8.2874 | 18.1298 | 0.1710 | 1.4828 |
| 2 | -0,04 | 0 | 0 | 0.4609 | 9.8100 | 19.5541 | 0.3417 | 1.6483 |
| 3 | 0,04 | 0 | 0 | 0.3853 | 6.7568 | 16.7055 | 0.0003 | 1.3173 |
| 4 | 0 | -0,2 | 0 | 0.4223 | 8.2331 | 18.0510 | 0.1535 | 1.4482 |
| 5 | 0 | 0,2 | 0 | 0.4239 | 8.3336 | 18.2086 | 0.1886 | 1.5174 |
| 6 | 0 | 0 | -0,2 | 0.4255 | 8.2380 | 17.9598 | 0.1954 | 1.5221 |
| 7 | 0 | 0 | 0,2 | 0.4208 | 8.3288 | 18.2998 | 0.1466 | 1.4435 |
Рекомендации по использованию результатов моделирования
После исследования данной имитационной модели массового обслуживания и ее анализа, были получены следующие данные, о том что коэффициент использования системы с тремя заданными параметрами равен 46%, среднее время ожидания 19 секунды, средняя задержка в очереди 9,2 секунды, среднее по времени количество требований в очереди 0,56, среднее по времени количество требований в системе 2,24.
Полученные выходные параметры, свидетельствует о том, что смоделированная нами система массового обслуживания является недогруженной и не достаточно эффективной.
Опираясь на анализ выходных данных моделирования можно сделать следующий вывод: система массового обслуживания будет достаточно эффективной при коэффициенте использования системы 79,9%, который достигается при минимальном количестве устройств равном 1, минимальном времени поступления требования равным 11 секунд и максимальном времени обработки требования равным 9 секунд. При таких входных параметрах системы мы получим среднее время ожидания равное 40 секундам, среднюю задержку в очереди 31,8, среднее по времени количество требований в очереди 2,5, среднее по времени количество требований в системе 3,4.
Следует отметить, что увеличение показателей среднего времени ожидания, средней задержки в очереди, среднего по времени количества требований в очереди и среднего по времени количества требований в системе являются допустимыми для достижения оптимального коэффициента использования системы.
Графики рекомендуемых параметров (коэффициент использования системы, по времени числа требований в очереди и системе) представлены в приложении A на рисунках А.9 и А.10.
Заключение
В процессе роботы над курсовым проектом «Построение и использование имитационных моделей» была разработана и создана программа имитационной модели системы массового обслуживания с циклической дисциплиной с квантом q, тремя входными факторами и пятью выходными параметрами. Задачи, поставленные в ходе курсового проекта, считаются выполненными. На основе статистического анализа выходных данных были даны рекомендации по выбору оптимальных параметров системы.
Список литературы
1. Кельтон В., Лоу А. Имитационное моделирование. Классика CS. 3-ие изд. – СПб.: Питер; Киев: Издательская группа BHV, 2008.
2. Советов Б.Я.Моделирование систем: Учебник для вузов 3-е изд., стер. - М.: Высшая школа.,2009.-295с.
3. Крылов Н.П., Самосвалов И.Т. Учебник по имитационному моделированию экономических процессов. 3-е изд, - Москва 2009- 458с.
4. Труб И.И. Объектно-ориентированное моделирование на C++, издательство СПб.: Питер; 2008- 346с.
Приложение А
На рисунках А.1, А.2, А.3, А.4, А.5, А.6, А.7, А.8 приведены графики контрольных прогонов для каждого эксперимента факторного плана представлены
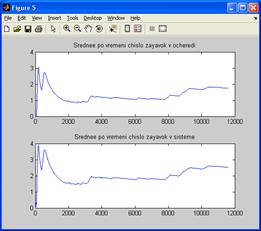
Рисунок А.1 – Среднее число требований в очереди и системе для факторов m=1, 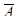 =11,
=11, 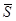 =8
=8
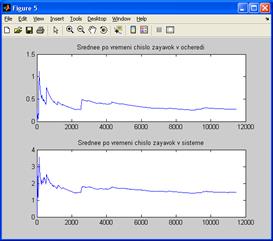
Рисунок А.2 – Среднее число требований в очереди и системе для факторов m=2, 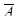 =11,
=11, 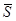 =8
=8
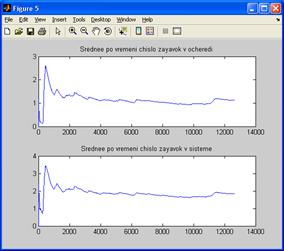
Рисунок А.3 – Среднее число требований в очереди и системе для факторов m=1, 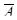 =12,
=12, 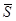 =8
=8
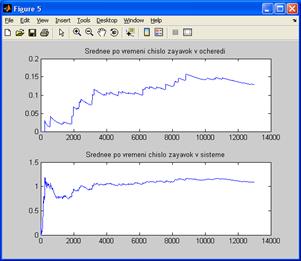
Рисунок А.4 – Среднее число требований в очереди и системе для факторов m=2, 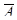 =12,
=12, 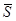 =8
=8
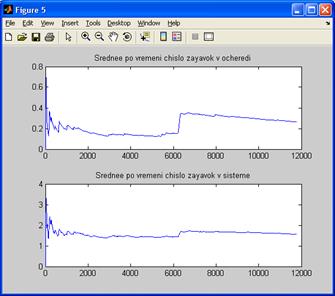
Рисунок А.5 – Среднее число требований в очереди и системе для факторов m=21, 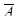 =11,
=11, 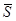 =9
=9

Рисунок А.6 – Среднее число требований в очереди и системе для факторов m=1, 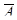 =12,
=12, 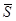 =9
=9
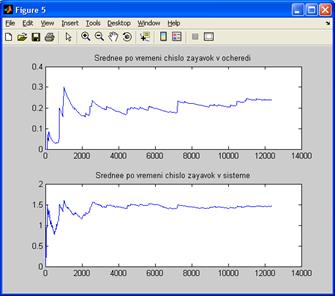
Рисунок А.7 – Среднее число требований в очереди и системе для факторов m=2, 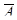 =12,
=12, 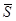 =9
=9
Так же рекомендуемыми параметрами использования системы являются параметры, указанные на графике А.9
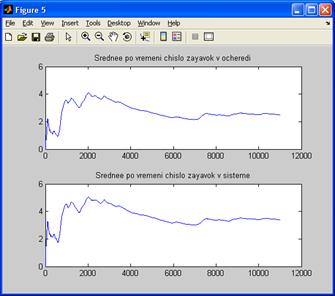
Рисунок А.9 – Рекомендуемые параметры использования системы m=1, 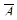 =11,
=11, 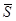 =9
=9
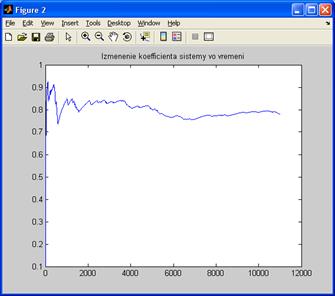
Рисунок А.9 – Рекомендуемый параметр коэффициента использования системы
Приложение Б
Расчет коэффициентов уравнения регрессии для коэффициента использования системы представлены ниже.
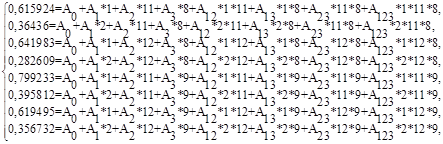
где 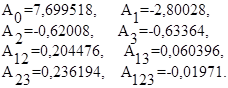
Для всех остальных выходных параметров коэффициенты уравнения регрессии рассчитываются аналогично.
Дата: 2019-05-28, просмотров: 307.