Для многих реальных процессов поток требований достаточно хорошо описывается законом распределения Пуассона. Такой поток называется простейшим.

Простейший поток обладает такими важными свойствами:

1) Свойством стационарности, которое выражает неизменность вероятностного режима потока по времени. Это значит, что число требований, поступающих в систему в равные промежутки времени, в среднем должно быть постоянным. Например, число вагонов, поступающих под погрузку в среднем в сутки должно быть одинаковым для различных периодов времени, к примеру, в начале и в конце декады.

2) Отсутствия последействия, которое обуславливает взаимную независимость поступления того или иного числа требований на обслуживание в непересекающиеся промежутки времени. Это значит, что число требований, поступающих в данный отрезок времени, не зависит от числа требований, обслуженных в предыдущем промежутке времени. Например, число автомобилей, прибывших за материалами в десятый день месяца, не зависит от числа автомобилей, обслуженных в четвертый или любой другой предыдущий день данного месяца.

3) Свойством ординарности, которое выражает практическую невозможность одновременного поступления двух или более требований (вероятность такого события неизмеримо мала по отношению к рассматриваемому промежутку времени, когда последний устремляют к нулю).

Таким образом, при моделировании мы генерируем две экспоненциально распределенные псевдослучайные последовательности с заданными средними значениями , .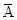

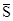Чтобы смоделировать экспоненциально распределенную случайную величину сначала генерируется стандартно равномерно распределенная случайная величина U, которая затем преобразуется в величину с экспоненциальным законом распределения согласно формуле:

X = –b ln(U),(2.1)

где b - математическое ожидание.

Для генерации стандартно равномерно распределенной случайной величины U используется мультипликативный генератор:

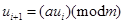, (2.2)

где: a = 630360016, m = 2147483647.

Рассмотрим вид входных распределений на основе последовательностей из 1000 элементов с входными параметрами генераторов ( 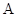– случайная величина поступления требований (среднее значение 10), 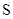– случайная величина обработки требований (среднее значение 10)):

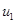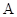( ) =46382 , 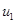( 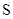) = 94215.

Оценка входных параметров

Оценки средних значений

Оценка математического ожидания случайных величин X вычисляется по формуле:

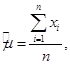
(3.1)

где n – количество элементов.

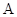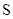Для случайных величин  и  она равна:

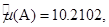
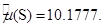
Оценка дисперсии случайных величин вычисляется по формуле:

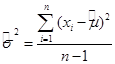.                                (3.2)

Для случайных величин 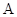 и 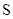она равна:

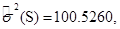
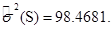
Оценка корреляции случайных величин вычисляется по формулам:

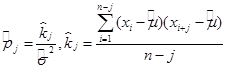,          (3.3)

где j = 1,…,n.

Графики корреляции показаны на рисунках 3.1. и 3.2.

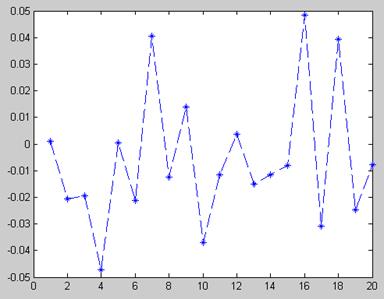
Рисунок 3.1 – Корреляция величины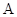

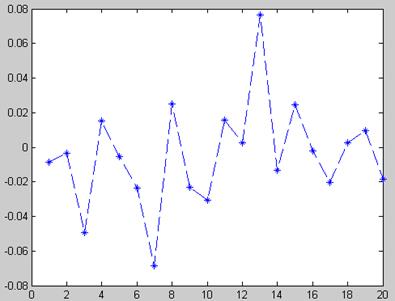
Рисунок 3.2 – Корреляция величины S

Графики зависимости последующего значения от предыдущего представлены на рисунках 3.3 и 3.4.

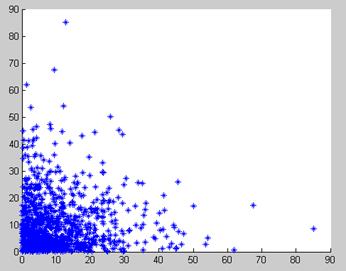
Рисунок 3.3 – Зависимость 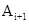 от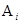

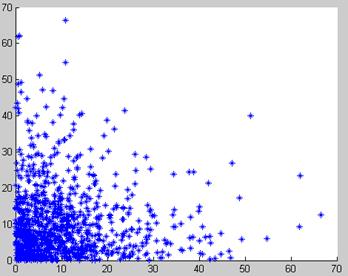
Рисунок 3.4 – Зависимость 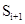 от

Интервальные оценки

Доверительный интервал для оценки математического ожидания случайной величины определяется формулой:

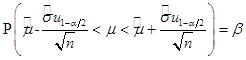, (3.4)

где b = 0.95 – доверительная вероятность, 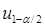 - квантиль порядка 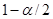,  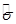=  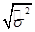- оценка дисперсии.  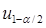= 1.96 для доверительной вероятности 0.95.

Доверительные интервалы для оценки математического ожидания случайных величин 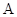 и 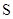 равны:

(9.5886; 10.8315), 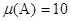– попадает в полученный доверительный интервал;

(9.5627; 10.7928), 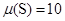– попадает в полученный доверительный интервал.