С началом изучения систематического курса алгебры основное внимание уделяется способам решения квадратных уравнений, которые становятся специальным объектом изучения. Для этой темы характерна большая глубина изложения и богатство устанавливаемых с ее помощью связей в обучении, логическая обоснованность изложения. Поэтому она занимает исключительное положение в линии уравнений и неравенств. К изучению этой темы учащиеся приступают, уже накопив определенный опыт, владея достаточно большим запасом алгебраических и общематематических представлений, понятий, умений.

Умение решать квадратные уравнения служит базой для решения других уравнений и их систем (дробных рациональных, иррациональных, высших степеней).

Для того чтобы решить любое квадратное уравнение, учащиеся должны знать:

· формулу нахождения дискриминанта;

· формулу нахождения корней квадратного уравнения;

· алгоритмы решения уравнений данного вида.

уметь:

· решать неполные квадратные уравнения;

· решать полные квадратные уравнения;

· решать приведенные квадратные уравнения;

· находить ошибки в решенных уравнениях и исправлять их;

· делать проверку.

Решение каждого уравнения складывается из двух основных частей:

· преобразования данного уравнения к простейшим;

· решения уравнений по известным правилам, формулам или алгоритмам.

При изучении темы «Квадратные уравнения» рассматриваются неполные, полные и приведенные квадратные уравнения. Для изучения данной темы были проанализированы современные школьные учебники разных авторов, таких как А.Г.Мордкович, С.М.Никольский, Ю.Н.Макарычев, М.И.Башмаков.

Анализ учебников

А.Г.   Мордкович	С.М. Никольский	Ю.Н. Макарычев	М.И. Башмаков
1. - 2.Неполные квадратные уравнения	1. -   2.Неполные квадратные уравнения	1. -   2.Неполные квадратные уравнения	1.Историческая справка   2.Неполные квадратные уравнения
3.Полные квадратные уравнения	3.Полные квадратные уравнения	3.Полные квадратные уравнения	3.Полные квадратные уравнения
4.Приведенные квадратные уравнения	4.Приведенные квадратные уравнения	4.Приведенные квадратные уравнения	4.Приведенные квадратные уравнения
	5.Теорема Виета	5.Теорема Виета
	6.Теорема, обратная теореме Виета	6.Теорема обратная теореме Виета

Исходя из таблицы можно сделать вывод о том, что в учебниках алгебры разных авторов есть сходства и различия. Во всех современных школьных учебниках алгебры методическая линия изучения квадратных уравнений одинакова. В учебнике под ред. М.И.Башмакова дается историческая справка, а в других учебниках этого нет. В учебниках алгебры С.М.Никольского и Ю.Н.Макарычева при изучении темы «Квадратные уравнения» рассматриваются прямая и обратная теорема Виета.

Обучение решению уравнений начинается с простейших их видов, и программа [4,131] обусловливает постепенное накопление как их видов, так и «фонда» тождественных и равносильных преобразований, с помощью которых можно привести произвольное уравнение к простейшим. В этом направлении следует строить и процесс формирования обобщенных приемов решения уравнений в школьном курсе алгебры. В курсе математики старших классов учащиеся сталкиваются с новыми классами уравнений, систем или с углубленным изучением уже известных классов. Однако это мало влияет на уже сформированную систему знаний, умений и навыков; они дополняют ее новым фактическим содержанием.

Обобщение способов деятельности учащихся при решении квадратных уравнений происходит постепенно. Можно выделить следующие этапы при изучении темы «Квадратные уравнения»:

I этап – «Решение неполных квадратных уравнений».

II этап – «Решение полных квадратных уравнений».

III этап – «Решение приведенных квадратных уравнений».

На первом этапе рассматриваются неполные квадратные уравнения. Так как сначала математики научились решать неполные квадратные уравнения, поскольку для этого не пришлось, как говорится, ничего изобретать. Это уравнения вида: ах² = 0, ах² + с = 0, где с≠ 0, ах² + bх = 0, где b ≠ 0. Рассмотрим решение несколько таких уравнений:

1. Если ах² = 0. Уравнения такого вида решаются по алгоритму:

1) найти х²;

2) найти х.

 Например, 5х² = 0 . Разделив обе части уравнения на 5 получается: х² = 0, откуда х = 0.

2. Если ах² + с = 0, с≠ 0 Уравнения данного вида решаются по алгоритму:

1) перенести слагаемые в правую часть;

2) найти все числа, квадраты которых равны числу с.

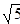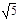Например, х² - 5 = 0,Это уравнение равносильно уравнению х²  = 5. Следовательно, надо найти все числа, квадраты которых равны числу 5. Таких чисел только два  и - .  Таким образом, уравнение  х² - 5 = 0 имеет два корня: x₁ =  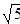,  x₂ = -  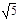 и других корней не имеет.

3. Если  ах² + bх = 0, b ≠ 0. Уравнения такого вида решаются по алгоритму:

1) перенести общий множитель за скобки;

2) найти x₁, x₂.

Например, х² - 3х = 0. Перепишем уравнение х² – 3х = 0 в виде х ( х – 3 ) = 0. Это уравнение имеет, очевидно, корни x₁ = 0, x₂ = 3. Других корней оно не имеет, ибо если в него подставить вместо х любое число, отличное от нуля и 3, то в левой части уравнения х ( х – 3 ) = 0 получится число, не равное нулю.

Итак, данные примеры показывают, как решаются неполные квадратные уравнения:

1) если уравнение имеет вид  ах² = 0, то оно имеет один корень х = 0;

2) если уравнение имеет вид ах² + bх = 0, то используется метод разложения на множители: х (ах +b) = 0; значит, либо х = 0, либо ах + b = 0. В итоге получается два корня: x₁ = 0; x₂ = - ;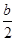

3) если уравнение имеет вид ах² + с = 0, то его преобразуют к виду ах² = - с и далее х².= - 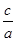 В случае, когда - 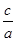< 0, уравнение х² = - 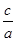не имеет корней (значит, не имеет корней и исходное уравнение ах² + с = 0). В случае, когда -  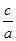> 0, т.е. -  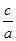= m , где m>0, уравнение х² = m имеет два корня

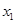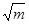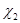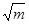 = ,  = - , (в этом случае допускается более короткая запись = .

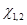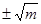Таким образом, неполное квадратное уравнение может иметь два корня, один корень, ни одного корня.

На втором этапе осуществляется переход к решению полного квадратного уравнения. Это уравнения вида ах² + bx + c = 0, где a,b,c – заданные числа, а ≠ 0, х – неизвестное.

Любое полное квадратное уравнение можно преобразовать к виду 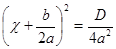 , для того, чтобы определять число корней квадратного уравнения и находить эти корни. Рассмотриваются следующие случаи решения полных квадратных уравнений: D < 0, D = 0, D > 0.

1. Если D < 0, то квадратное уравнение ах² + bx + c = 0 не имеет действительных корней.

Например, 2х² + 4х + 7 = 0. Решение: здесь а = 2, b = 4, с = 7.

D = b² – 4ас = 4² – 4*2*7 = 16 – 56 = - 40.

Так как D < 0, то данное квадратное уравнение не имеет корней.

2. Если D = 0, то квадратное уравнение ах² + bx + c = 0 имеет один корень, который находится по формуле .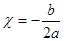

Например, 4х – 20х + 25 = 0. Решение: а = 4, b = - 20, с = 25.

D = b² – 4ас = (-20) ² – 4*4*25 = 400 – 400 = 0.

Так как D = 0, то данное уравнение имеет один корень. Этот корень находится по формуле 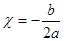. Значит,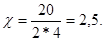  

3. Если D > 0, то квадратное уравнение ах² + bx + c = 0 имеет два корня, которые находятся по формулам: 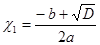;  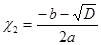                        (1)

Например, 3х² +8х – 11 = 0. Решение: а = 3, b = 8, с = -11. D = b² – 4ас = 8²  – 4*3*(-11) = 64 + 132 = 196.

Так как D > 0, то данное квадратное уравнение имеет два корня. Эти корни находятся по формулам:

.

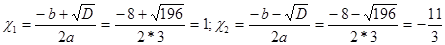Составляется алгоритм решения уравнения вида ах² + bx + c = 0.

1. Вычислить дискриминант D по формуле D = b² – 4ас.

2. Если D < 0, то квадратное уравнение ах² + bx + c = 0 не имеет корней.

3. Если D = 0, то квадратное уравнение имеет один корень, который находится по формуле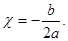

4. Если D > 0, то квадратное уравнение ах² + bx + c = 0 имеет два корня:  ; .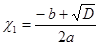

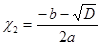Это алгоритм универсален, он применим как к неполным, так и к полным квадратным уравнениям. Однако неполные квадратные уравнения обычно по этому алгоритму не решают.

Математики – люди практичные, экономные, поэтому пользуются формулой: 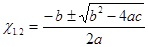. (2)

Итак, можно сделать вывод, что квадратные уравнения можно решать подробно, используя сформулированное выше правило; можно – записать сразу формулу (2) и с ее помощью делать необходимые выводы. [1,98].

На третьем этапе рассматриваются приведенные квадратные уравнения, которые имеют вид х² +px + q = 0 (3), где p и q – данные числа. Число p – коэффициент при х, а q – свободный член. Дискриминант уравнения равен: D = p² – 4q. Рассматривают 3 случая:

1. D > 0, тогда уравнение (3) имеет два корня, вычисляемые по формуле 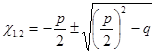. (4)

2. D = 0, тогда уравнение (3) имеет единственный корень, или, как горят, два совпадающих корня: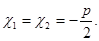

3. D < 0, то уравнение не имеет корней. Обычно в случае приведенного квадратного уравнения (3) вместо D рассматривается выражение 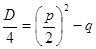, имеющее тот же знак, что и D. При этом формулу корней приведенного квадратного уравнения (4) записывают так: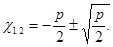

Отсюда следует, что:

1) если 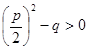 то уравнение (3) имеет два корня;

2) если 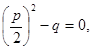 то уравнение имеет два совпадающих корня;

3) если 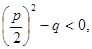 то уравнение не имеет корней.

Важным моментом в изучении квадратных уравнений является рассмотрение теоремы Виета, которая утверждает наличие зависимости между корнями и коэффициентами приведенного квадратного уравнения.

Теорема Виета. Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Иначе говоря, если x₁  и x₂ - корни уравнения х² +px + q = 0, то

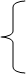
                                       x₁ + x₂  = - p,

                                       x₁ x₂ = q.                         (5)

Данные формулы называют формулами Виета в честь французского математика Ф.Виета (1540-1603), который ввел систему алгебраических символов, разработал основы элементарной алгебры. Он был одним из первых, кто числа стал обозначать буквами, что существенно развило теорию уравнений.

Например, приведенное уравнение х² - 7х +10 = 0 имеет корни 2 и 5. Сумма корней равна 7, а произведение равно 10. Видно, что сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Справедлива также теорема, обратная теореме Виета.

Теорема, обратная теореме Виета. Если для чисел x₁, x_2, p, q справедливы формулы (5), то x₁ и x₂ - корни уравнения х² +px + q = 0 [2,49].

Теорема Виета и теорема, обратная ей, часто применяются при решении различных задач.

Например. Напишем приведенное квадратное уравнение, корнями которого являются числа 1 и -3.

По формулам Виета

– p = x₁ + x₂ = - 2,

q = x₁ x₂  = -3.

Следовательно, искомое уравнение имеет вид х² + 2х – 3 = 0.

Сложность освоения теоремы Виета связана с несколькими обстоятельствами. Прежде всего, требуется учитывать различие прямой и обратной теоремы. В прямой теореме Виета даны квадратное уравнение и его корни; в обратной — только два числа, а квадратное уравнение появляется в заключении теоремы. Учащиеся часто совершают ошибку, обосновывая свои рассуждения неверной ссылкой на прямую или обратную теорему Виета.

Например, при нахождении корней квадратного уравнения подбором ссылаться нужно на обратную теорему Виета, а не на прямую, как часто делают учащиеся. Для того чтобы распространить теоремы Виета на случай нулевого дискриминанта, приходится условиться, что в этом случае квадратное уравнение имеет два равных корня. Удобство такого соглашения проявляется при разложении квадратного трехчлена на множители

Таким образом, неполные и приведенные квадратные уравнения имеют разные алгоритмы решения, при изучении данной темы необходимо показать, что общая формула корней применима и для этих случаев. Обычно они изучаются перед выводом корней общего квадратного уравнения. В целом можно сказать, что освоение темы «Квадратные уравнения» поднимает учащихся на качественно новую ступень овладения содержанием школьной математики.