МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАІНИ
Бердянський державний педагогічний університет
фізико-математичний факультет
Кафедра математики,
методики викладання математики
Курсова робота
Методика проведення лабораторних занять з курсу
«Застосування ІКТ у навчальному процесі з математики»
Студентки 6 курсу
Заочної форми навчання
Васильєвої Інесси Сергіївни
Науковий керівник:
Ачкан В.В.
Бердянськ
2011
ЗМІСТ
РОЗДІЛ І
ТЕОРЕТИЧНІ ЗАСАДИ З КУРСУ «ЗАСТОСУВАННЯ ІКТ У ПРОЦЕСІ НАВЧАННЯ МАТЕМАТИКИ»
І.1 Роль та місце ІКТ при підготовці майбутніх вчителів математики
І.2 Лабораторні заняття як форма організації процесу навчання математики
І.3 Психолого—педагогічні основи вивчення курсу «Застосування ІКТ у процесі навчання математики»
ВИСНОВКИ РОЗДІЛУ І
РОЗДІЛ ІІ
КОМПОНЕНТИ МЕТОДИЧНОЇ СИСТЕМИ НАВЧАННЯ З КУРСУ «ЗАСТОСУВАННЯ ІКТ У ПРОЦЕСІ НАВЧАННЯ МАТЕМАТИКИ»
ІІ.1 Методичні вимоги щодо вибору навчальної програми з курсу «Застосування ІКТ у процесі навчання математики»
ІІ.2 Сучасні ППЗ та профільні математичні засоби у навчальному процесі
ІІ.3 Методична розробка лабораторних занять Змістовного модуля 4. «Програмні засоби у навчанні математики» з курсу «Застосування ІКТ у процесі навчання математики»
ВИСНОВКИ РОЗДІЛУ ІІ
ВИСНОВКИ
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
ВСТУП
Однією з основних задач як вищої, так і середньої школи сьогодні є підготовка школярів та студентів до життя в інформатизованому суспільстві. Інформаційну культуру потрібно розглядати як невід'ємну складову загальної культури та освіти фахівця. Під час формування інформаційного суспільства комп'ютер стає звичайним робочим інструментом фахівця будь–якої галузі діяльності.
Серед всіх навчальних дисциплін в педагогічному університеті особливе місце належить курсу математики. Вивчення курсу математики формує науковий світогляд, розуміння сутності прикладних проблем, дозволяє оволодіти методами математичного моделювання. У педагогічних ВНЗ особливої уваги потребує підготовка вчителя математики, тому що математика є одним із провідних предметів у системі шкільної і вузівської освіти.
Вимоги до математичної освіти на сучасному етапі зазнали деяких змін, а саме: зменшилася кількість годин, що відводилися на класичний аналіз, алгебру, геометрію. Вводяться нові навчальні дисципліни, поява яких продиктована практичною необхідністю прикладного застосування математики. Введення у навчальний процес цих дисциплін неможливе без застосування сучасних інформаційно–комунікаційних технологій (ІКТ), а головне — спеціалізованих математичних пакетів та програм навчального призначення.
Використання інформаційно-комунікаційних технологій має бути педагогiчно виправданим, розглядатись передусiм з точки зору педагогiчних переваг, якi воно може дати порiвняно з традицiйною методикою. Для успiшного застосування IКТ при вивченнi курсу математики в педагогічних університетах необхiдно внести певні змiни в методику навчання даного предмета. Програмна пiдтримка курсу математики повинна сприяти досягненню педагогiчних цілей за рахунок використання комп'ютерних засобiв для iлюстрацiї математичних понять, демонстрацiї застосувань математичних методiв дослiдження рiзноманiтних процесiв i явищ, проведення чисельного експерименту, створення та вивчення iнформацiйних i математичних моделей різноманітних явищ i процесiв, проведення комп'ютерних експериментів у геометрії.
Все ширше використовуються комп'ютери та чисельні методи для розв'язування прикладних задач. Вимоги чисельного розв'язування прикладних задач привели до появи великої кількості нових методів. Відбувається інтенсивне теоретичне переосмислення як традиційних, так і нових чисельних методів та їх систематизація.
Сьогодні вже накопичено значний досвід використання сучасних IКТ в навчальному процесі школи та ВНЗ, який висвітлено в працях Н.В.Апатової, Н.Р.Балик, В.Г.Болтянського, А.Ф.Верланя, О.М.Довгяло, А.П.Єршова, М.І.Жалдака, Л.В.Занкова, Т.Б.Захарова, О.А.Кузнєцова, В.І.Клочка, В.М.Монахова, Н.В.Морзе, С.А.Ракова, Ю.С.Рамського, В.Г.Розумовського, Ю.В.Триуса та інших.
При підготовці вчителя математики необхідно враховувати "специфічні закони, закономірності, принципи, особливості і умови освіти, навчання, виховання та формування особистості професіонала". Розглядаючи характер і зміст праці фахівців в умовах науково–інформаційного суспільства, потрібно враховувати засоби професійної діяльності фахівця. В умовах широкого використання засобів ІКТ такими інструментами виступають математичні пакети, що створювалися для фахівців–математиків. Математичні пакети можна використовувати і для навчання, тобто як педагогічні програмні засоби. Різні аспекти використання математичних пакетів як технічні, так і дидактичні розглядаються в працях таких вчених, як В.З.Аладьєв, М.Л.Шишаков, В.П.Дьяконов, Т.В.Капустіна, Ю.Ф.Лазарев, Б.М.Манзон, В.Ф.Очков, В.Г.Потьомкін та інших.
В Україні в напрямі інформатизованих систем навчання математики активно працює школа академіка АПН М.І.Жалдака – Є.Ф.Вінниченко, О.В.Вітюк, М.С.Головань, Ю.В.Горошко, Т.В.Зайцева, В.І.Клочко, І.В.Лупан, Г.О.Михалін , Н.В.Морзе, А.В.Пеньков, Ю.С.Рамський, О.А.Смалько, Є.М.Смірнова, Ю.В.Триус, Т.І.Чепрасова, А.М.Ясинський та інші.
Попри велике наукове i практичне значення проведених досліджень ряд аспектів потребує подальшого вивчення. Зокрема, недостатньо розроблені питання методики навчання дисциплін математичного циклу із застосуванням ІКТ у ВНЗ педагогічного профілю.
Все більш зростаючі вимоги до підготовки майбутнього вчителя математики, необхідність наблизити його підготовку до сучасних вимог щодо педагогічної діяльності потребує перегляду методичної системи навчання математики в університетах та педагогічних ВНЗ. З появою та впровадженням в практику навчання математики сучасних засобів ІКТ намітилися досить суттєві зрушення у розв'язанні даної проблеми.
Об'єктом дослідження є комп'ютерно–орієнтована методична система навчання методиці математики у вищих педагогічних навчальних закладах.
Предметом дослідження є процес вивчення студентів курсу “Застосування ІКТ в процесі навчання математики»
Мета дослідження — Розробити методичні рекомендації проведення лабораторних занять з курсу “Застосування ІКТ в процесі навчання математики»
Завдання дослідження :
проаналізувати стан досліджуваної проблеми, виявити можливості вдосконалення методичної системи навчання математики в педагогічному ВНЗ за рахунок широкого впровадження засобів ІКТ в навчальний процес;
дібрати необхідні математичні пакети для впровадження у навчальний процес, виконати розробки для комп'ютерної підтримки навчально–пізнавальної діяльності студентів при навчанні математики, розробити плани — конспекти лабораторних занять.
Методи дослідження :
теоретичний аналіз науково–методичної та психолого–педагогічної літератури з проблеми дослідження;
аналіз ППЗ та професійних математичних пакетів на предмет їх використання в навчальному процесі;
співбесіди з викладачами, які проводять лекційні та практичні заняття з математики.
РОЗДІЛ І ТЕОРЕТИЧНІ ЗАСАДИ З КУРСУ «ЗАСТОСУВАННЯ ІКТ У ПРОЦЕСІ НАВЧАННЯ МАТЕМАТИКИ»
СЕМЕСТР (4 кредити) – залік
| Тема | Кількість годин відведених на | |||||
| Лекції | Лабораторні заняття | Самостій-ну роботу | Індивіду-альну роботу | |||
| Змістовий модуль 1. Вступ. Інформаційно-комунікаційні технології у сучасній освіті. | ||||||
| Тема 1. Поняття інформаційно- комунікаційних технологій та їх місце у сучасній освіті. | 2 |
| ||||
| Тема 2. Роль та місце інформаційно-комунікаційних технологій у навчанні математики. | 2 | 1 | ||||
| Тема 3. Психолого-педагогічні аспекти застосування інформаційно-комунікаційних технологій навчання математики. | 2 | 1 | ||||
| Тема 4. Методичні можливості, що надає використання ІКТ у навчанні математики. | 2 | 2 | ||||
| Всього годин | 8 | 4 | ||||
| Змістовий модуль 2. Використання редактору формул, електронних таблиць та інтернет-ресурсів у підготовці методичного забезпечення вчителя математики | ||||||
| Тема 5. Редактор формул Equations та його використання у підготовці дидактичних матеріалів та завдань для моніторингу. | 2 | 4 | ||||
| Тема 6. Використання електронних таблиць у підготовці дидактичних матеріалів та завдань для моніторингу. | 2 | 4 | ||||
| Тема 7. Використання інтернет-ресурсів у підготовці вчителя математики до уроку та на уроці. | 2 | 4 | ||||
| Всього годин | 6 | 12 | ||||
| Змістовий модуль 3. Мультимедійні засоби навчання математики. | ||||||
| Тема 8. Презентації MS Power Point у навчальному процесі. | 2 | 2 | ||||
| Тема 9. Педагогічні вимоги щодо структури та змісту презентації | 2 | 2 | ||||
| Тема 10. Створення навчальних презентацій. | 2 | 6 | ||||
| Тема 11. Використання навчальних презентацій при проведенні різних організаційних форм навчання математики | 2 | 4 | ||||
| Всього годин | 12 | 14 | ||||
| Змістовий модуль 4. Програмні засоби у навчанні математики. | ||||||
| Тема 12. Класифікація математичних пакетів (навчального призначення та професійних). | 2 | 2 | ||||
| Тема 13. Педагогічних програмний засіб GRAN 1 | 1 | 2 | ||||
| Тема 14. Педагогічних програмний засіб GRAN 2 | 1 | 2 | ||||
| Тема 15. Педагогічних програмний засіб GRAN 3 | 1 | 2 | ||||
| Тема 16. Педагогічних програмний засіб DG | 1 | 2 | ||||
| Тема 17. Педагогічні програмні засоби "Математика, 5 клас", ТерМ-7. | 1 | 2 | ||||
| Тема 18. Педагогічні програмні засоби Алгебра 7-9, Schooltools. | 1 | 2 | ||||
| Тема 19. Математичні програмні засоби Matcad, Matlab. | 1 | 2 | ||||
| Тема 20. Математичні програмні засоби Maple, Mathematica. | 1 | 2 | ||||
| Всього годин | 10 | 18 | ||||
| Змістовий модуль 5 . Використання ІКТ у процесі навчання математики в основній школі. | ||||||
| Тема 21. Комп'ютерно-орієнтоване тематичне планування тем. | 2 | 2 | ||||
| Тема 22. Використання ІКТ у процесі вивчення математики у 5-6 класах | 1 | 6 | ||||
| Тема 23. Використання ІКТ на уроках алгебри у 7-9 класах. | 1 | 6 | ||||
| Тема 24. Використання ІКТ на уроках геометрії у 7-9 класах | 1 | 6 | ||||
| Всього годин | 12 | 12 | ||||
| Змістовий модуль 5. Стереометрія | ||||||
| Тема 23. Паралельність та перпендикулярність прямих і площин у просторі | 2 | 2 | ||||
| Тема 24. Вектори, координати та геометричні перетворення у просторі | 2 | 2 | ||||
| Тема 25. Геометричні тіла та поверхні. Многогранники | 2 | 2 | ||||
| Тема 26. Геометричні тіла та поверхні. Тіла обертання | 2 | 2 | ||||
| Тема 27. Комбінації геометричних тіл | 2 | 2 | ||||
| Всього годин | 10 | 10 | ||||
| Всього годин за 1 семестр | 48 | 48 | ||||
| тема | Лекції | Лабораторні роботи | Самостійна робота | ||
| Вступ. Інформаційно-комунікаційні технології та їх застосування у навчанні математики. | 2 |
| 2 | ||
| Заліковий кредит 1. Комп'ютерно-орієнтоване навчання математики | |||||
| Змістовий модуль 1. Комп'ютерно-орієнтована методична система навчання математики | 6 | 2 | 30 | ||
| Тема 1. Особливості комп'ютерно-орієнтованої методичної системи навчання математики. . Основні вимоги до організації навчання математики зі застосуванням ІКТ. | 2 |
| 6 | ||
| Тема 2. Напрямки використання ІКТ у навчанні математики. | 2 | 2 | 4 | ||
| Тема 3. Класифікація ІКТ і приклади їх застосування. | 2 |
| 20 | ||
| Заліковий кредит 2. Технології створення й опрацювання текстових і числових даних | |||||
| Змістовий модуль 2. Текстовий редактор | 6 | 8 | 38 | ||
| Тема 4. Поняття тексту і його обробки. Створення нового документа. Основні об'єкти в текстовому редакторі (символ, абзац, документ) та операції з ними. | 2 |
| 8 | ||
| Тема 5. Принципи форматування тексту. Форматування символів тексту: вибір шрифту, зміна розмірів літер, накреслення, кольору, встановлення ефектів. Форматування абзаців: зміна відступів, типу вирівнювання. Робота зі сторінками. Робота з фрагментами тексту: виділення, вставляння, переміщення, копіювання, вилучення, пошук і заміна фрагментів тексту. Використання буфера обміну. | 2 | 8 | |||
| Тема 6. Таблиці у навчанні. Види таблиць і їх цільове призначення. Вставляння таблиць до текстового документа. Форматування таблиць. | 2 | 2 | 8 | ||
| Тема 7. Робота з "графічними об'єктами в середовищі текстового редактора. Введення формул, оздоблення тексту. | 2 | 10 | |||
| Тема 8. Шаблони документів. Структура документа. | 2 | 2 | 4 | ||
| Змістовий модуль 3. Електронні таблиці | 2 | 4 | 20 | ||
| Тема 9. Електронні таблиці: призначення, основні можливості. Основні об'єкти в електронних таблицях і операції над ними (комірка, лист, книга). Введення чисел, формул і тексту. Абсолютна і відносна адресації комірок. Стандартні функції. Редагування і форматування таблиць. Побудова діаграм і графіків. | 2 | 2 | 12 | ||
| Тема 10. Використання електронних таблиць для створення дидактичних матеріалів,і завдань освітнього моніторингу. | 2 | 8 | |||
| Заліковий кредит 3. Мультимедійні технології у навчанні | |||||
| Змістовий модуль 4. Мультимедійні засоби навчання | 12 | 10 | 54 | ||
| Тема 11. Поняття комп'ютерної презентації. Загальні правила та педагогічні вимоги до створення текстів, рисунків, анімації і звуку на слайдах, гіперпосилань і систем навігації. | 4 |
| 10 | ||
| Тема 12. Створення навчальних презентацій. Педагогічний сценарій. | 4 | 6 | 20 | ||
| Тема 13. Проектування різних етапів уроку з використанням ІКТ | 4 | 4 | 24 | ||
| Змістовий модуль 5. Програмні засоби у навчанні математики | 8 | 12 | 54 | ||
| Тема 14. Програмні засоби цільового призначення. Комп'ютерні енциклопедії, довідники, словники, перекладачі, графобудівники. |
|
| 10 | ||
| Тема 15. Педагогічні програмні засоби навчання математики: СЖАШ, СЖАК-2Б, ОК/Ш-ЗБ, гЗо,ЕДК. | 4 | 6 | 20 | ||
| Тема 16. Програми універсального призначення для проведення тренувальних вправ або контролю знань учнів (ТегМ, евристичні тренажери, курси «Открьітая математика»). | 2 | 4 | 14 | ||
| Тема 17. Програми-шаблони (оболонки) для створення навчальних програм та методичного забезпечення уроків. | 2 | 2 | 10 | ||
| Разом | 36 | 36 | 198 | ||
4. Завдання для самостійної роботи
1. Створення дидактичних посібників з математики із використанням текстового процесора..
Попередня підготовка навчальних матеріалів, добір і структурування даних. Створення файлу. Набір тексту. Оформлення заголовків. Добір і сканування ілюстрацій. Набір формул. Створення рисунків з геометричними фігурами, з різноманітними графіками функцій. Друк посібників.
2. Введення і аналіз поточних і підсумкових результатів успішності учнів з використанням електронної таблиці М8 Ех cel . Побудова діаграм і графіків. Створення кросвордів.
Введення анкетних даних учнів до таблиці. Заповнення поточними оцінками. Складання підсумкових листів. Статистичний аналіз даних. Побудова діаграм і графіків на основі даних таблиць.
3. Створення тестів з математики
Ознайомлення з програмами-шаблонами (оболонками) для створення тренувальних вправ або контролю знань учнів. Принципи проектування комбінованої тестової програми з навчального предмета в середовищі М8 Excel. Логічні і арифметичні функції. Лист для показу підсумків тестування. Лист для розрахунків оцінок. Листи для формулювання питань. Налагодження Ех cel. Перевірка правильності складання тесту.
4. Створення мультимедійної презентації навчального матеріалу в середовищі М8 Р ower Роіп t
Педагогічний мультимедійний майстер-шаблон як зразок програмної реалізації навчального матеріалу. Гіпертекст. Технологія створення. Основні об'єкти майстер - шаблона. Текстові, графічні, звукові, відеослайди. Створення презентацій. Ієрархічна навігаційна структура педагогічного мультимедійного майстер-шаблона. Демонстрація презентацій.
5. Робота з педагогічними програмними засобами
Установка програм. Ознайомлення з правилами роботи і структурою. Аналіз ППЗ на предмет і напрямок доцільності використання на уроках. Складання відповідної системи вправ, задач, евристичних приписів.
ППЗ ОКАШ.. Побудова графіків функцій, заданих явно, неявно, параметрично, таблицею. Дослідження функцій. Побудова і дослідження кривих у полярних координатах. Графічне розв'язування рівнянь, нерівностей, їх систем. Дослідження рівнянь і нерівностей з параметрами. Площа криволінійної. трапеції. Обчислення інтегралів. Об'єм і площа (поверхні, тіла обертання). Опрацювання статистичних даних.
ППЗ ОКАШВ. Створення геометричні об'єктів на площині. Вимірювальні інструменти.
ППЗ (ЖА№Ю. Створення моделей просторових об'єктів. Обчислення характеристик елементів-многогранників і тіл обертання; площі поверхні та об'ємів тіл. Побудова перерізів многогранників площиною.
БО. Створення побудов за допомогою комп'ютерних аналогів циркуля та лінійки, дослідження отриманих результатів, проведення вимірювань. Створення наочних • ілюстрацій, інтерактивних і' динамічних навчальних посібників, довідників, використання коментарів, кнопок, підказувань і гіперпосилань. Організація елементів комп'ютерних експериментів і досліджень, висування і візуальна перевірка гіпотез.
ЕДК. Тестування. Ознайомлення з програмами «Задача-метод», «Задача-софізм», «Тест-корекція». Евристичні тренажери.
ІІ.2 Сучасні ППЗ та профільні математичні засоби у навчальному процесі
Основною і необхідною складовою інформаційних технологій навчання є педагогічні програмні засоби (ППЗ) або програмні засоби навчально-виховного призначення (ПЗНП). До ПЗНП можна віднести програмні засоби різного призначення, засоби навчання, що використовуються в поєднанні з обчислювальною технікою, відео- та аудіо-матеріали, гіпертекстові та гіпермедійні системи навчального призначення тощо.
Лабораторне заняття №1
З курсу «Застосування ІКТ у навчанні математики»
Тема. Педагогічний програмний засіб GRAN 1.
Навчально-матеріальне забезпечення. Персональні комп’ютери, програмне забезпечення Windows XP, ППЗ GRAN1.
Мета роботи. Отримати навички роботи з педагогічним програмним засобом GRAN1.
Завдання:
1. Виконати завдання.
2. Зберегти електронну версію отриманих результати.
3. Оформити звіт.
Звіт містить такі розділи:
- Титульний аркуш.
- Завдання роботи.
- Письмовий опис дій по виконанню завдань.
- Отримані результати.
Для роботи у програмі нам знадобляться деякі відомості.
1. Для того щоб створити нову функцію клікніть мишкою на кнопку у вікні «Список об’єктів» та виберіть ту функцію, яка вам потрібна. Потім клацніть правою кнопкою миші у цьому вікні і виберіть «створити».


Рис.1 Рис.2
 2. Для того щоб побудувати графік натисніть кнопку
2. Для того щоб побудувати графік натисніть кнопку
3. Для того щоб побудувати пряму х = к задаємо її як ламану, координати точок (к, в) (к, -в), в – будь яке число.
4. Для того щоб знайти площу поверхні та об’єм тіла навколо осі клацніть мишею на кнопку «Операції», виберіть інтеграл, а потім виберіть навколо якої осі відбувається обертання.
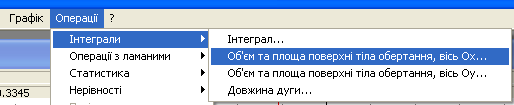
Рис.3
Примітка. Для того щоб записати |х| у програмі вводимо функцію Abs(x), щоб ввести 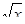 застосовуємо функцію Sqrt(x).
застосовуємо функцію Sqrt(x).
Практичні завдання
1. Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Ох функції 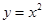 та прямими у= 0 та х = 3 .
та прямими у= 0 та х = 3 .
2. Знайти об’єм тіла, утвореного обертанням навколо осі Ох функції 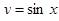 і прямими у = 0, х = 0, х =
і прямими у = 0, х = 0, х = 
3. Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Ох функції 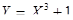 , у = 0, х = 2, х= 1.
, у = 0, х = 2, х= 1.
4. Знайти площу повної поверхні тіла, утвореного обертанням навколо осі Ох функції 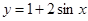 у = 0, х = 0 , х =
у = 0, х = 0 , х =  /2.
/2.
5. Знайти площу повної поверхні тіла, утвореного обертанням навколо осі Оу функції 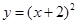 , у = 0, х = 0.
, у = 0, х = 0.
6. Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Оу функції 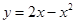 та у = 0.
та у = 0.
7. Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Оу функції 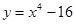 та у = 0
та у = 0
8. Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Оу функції 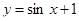 та
та 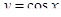 .
.
9. Розв’язати нерівність 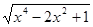 >
> 
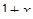 .
.
10.Побудувати графік функції 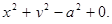
11.Побудувати графік функції 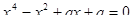
12.Побудувати графік функції 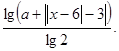
13.Побудувати графік функції 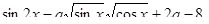 .
.
14.Вкажіть, скільки дійсних коренів має рівняння 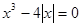
15.При яких значеннях параметра а нерівність 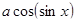 <0.
<0.
16.Обчислити інтеграл 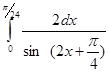 .
.
17.Обчислити інтеграл 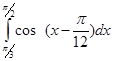 .
.
18.Обчислити інтеграл 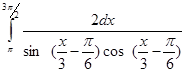 .
.
19.Обчислити інтеграл 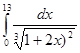 .
.
20.Обчислити інтеграл 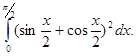
Розв’язання вправ
1. Знайти об’єм тіла та площу повної поверхні цього тіла, утвореного обертанням навколо осі Ох функцї 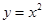 та прямими у = 0 та х = 3 .
та прямими у = 0 та х = 3 .
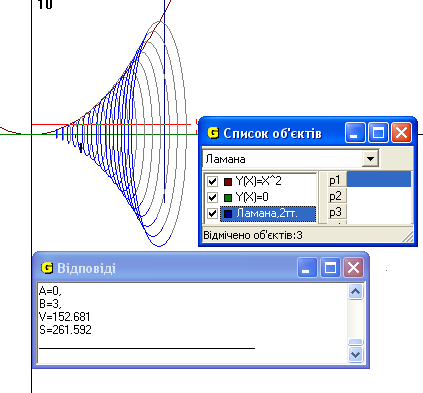
Рис.4
Відповідь: об’єм 152.682 од.куб., площа повної поверхні 261.592 од.кв. тіла утвореного обертанням навколо осі Ох функції 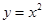 та прямими у = 0 та х = 3 (Рис4).
та прямими у = 0 та х = 3 (Рис4).
2. Знайти об’єм тіла, утвореного обертанням навколо осі Ох функції 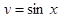 і прямими у = 0, х = 0, х =
і прямими у = 0, х = 0, х = 
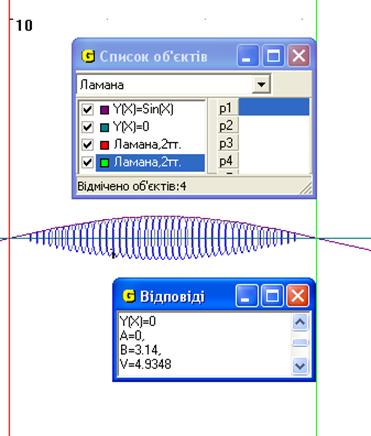
Рис.5
Відповідь: об’єм тіла утвореного обертанням навколо осі Ох функції 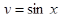 і прямими у = 0, х = 0, х =
і прямими у = 0, х = 0, х = 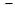 дорівнює 4.9348 од.куб (Рис.5).
дорівнює 4.9348 од.куб (Рис.5).
3. Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Ох функції 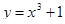 , у = 0, х = 2, х = 1.
, у = 0, х = 2, х = 1.
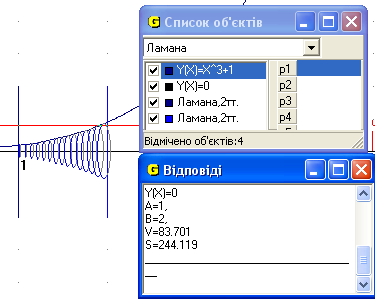
Рис.6
Відповідь: об’єм 83.701 од.куб. та площа повної поверхні 244.119 од.кв. тіла, утвореного обертанням навколо осі Ох функції 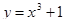 , у = 0, х = 2, х=1(Рис.6).
, у = 0, х = 2, х=1(Рис.6).
4. Знайти площу повної поверхні тіла, утвореного обертанням навколо осі Ох функції 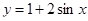 у = 0, х = 0 , х =
у = 0, х = 0 , х = 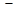 /2.
/2.
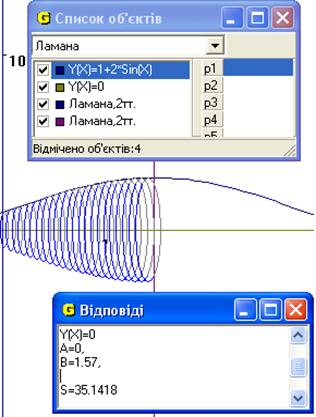
Рис.7
Відповідь: площа повної поверхні тіла, утвореного обертанням навколо осі Ох функції 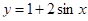 у = 0, х = 0 , х =
у = 0, х = 0 , х = 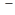 /2 дорівнює 35.1418 од.кв (Рис.7).
/2 дорівнює 35.1418 од.кв (Рис.7).
5. Знайти площу повної поверхні тіла, утвореного обертанням навколо осі Оу функції 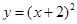 , у = 0, х = 0.
, у = 0, х = 0.
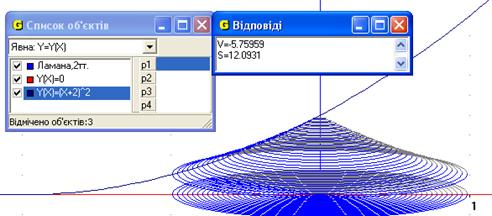
Рис.8
Відповідь: площа повної поверхні тіла, утвореного обертанням навколо осі Оу функції 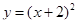 , у = 0, х = 0 дорівнює 12.1 од.кв (Рис.8).
, у = 0, х = 0 дорівнює 12.1 од.кв (Рис.8).
6. Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Оу функції 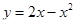 та у = 0.
та у = 0.
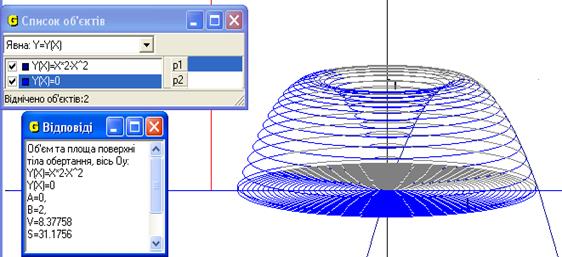
Рис.9
Відповідь: об’єм тіла 8.38 од.куб. та площ повної поверхні тіла, утвореного обертанням навколо осі Оу функції 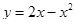 та у = 0 31.18 од.кв (Рис.9).
та у = 0 31.18 од.кв (Рис.9).
7. Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Оу функції 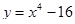 та у = 0.
та у = 0.
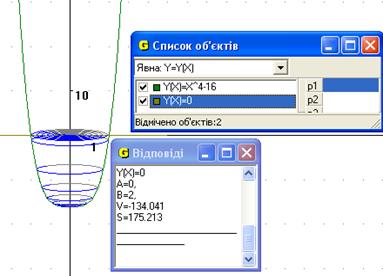
Рис.10
Відповідь: об’єм тіла 134 од.куб. та площа повної поверхні тіла, утвореного обертанням навколо осі Оу функції 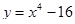 та у = 0 175.2 од.кв (Рис.10).
та у = 0 175.2 од.кв (Рис.10).
8. Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Оу функції 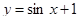 та
та 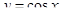 .
.
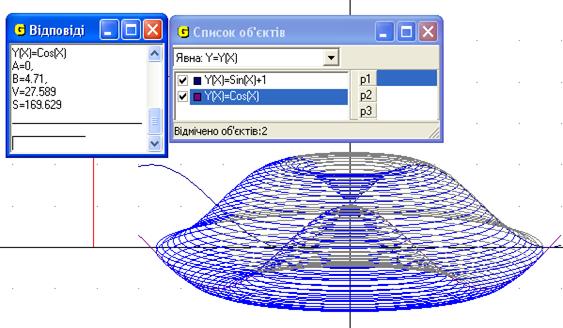
Рис.11
Відповідь: об’єм тіла 27.59 од.куб. та площа повної поверхні тіла, утвореного обертанням навколо осі Оу функції 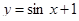 та
та 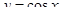 дорівнює 169.63 од.кв (Рис.11).
дорівнює 169.63 од.кв (Рис.11).
9. Розв’язати нерівність 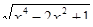 >
> 
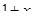 .
.
Будуємо графіки функцій f(x)= 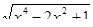 i
i  g(x)=
g(x)= 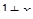 .(Рис.12)
.(Рис.12)
На екрані бачимо, що графіки функцій f(x) та g(x) перетинаються у трьох точках x = − 1; x = 0 та x = 2 . Перевіряємо чи є ці числа коренями рівняння 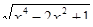 =
= 
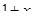 .
.
З’ясовуємо що розв’язками нерівності f(x)> (<) g(x) будуть ті значення аргументу, при яких графік функцій f(x) знаходиться вище (нижче) графіка функцій g(x). За допомогою графіка приходимо висновку, що задана нерівність виконується, якщо x ∈ (− ∞ ; − 1 ) ∪(− 1; 0 ) ∪(2; +∞ ).
Отже, маємо розв’язок: x ∈ (− ∞ ;−1) ∪(− 1; 0 )∪ (2; + ∞ ).
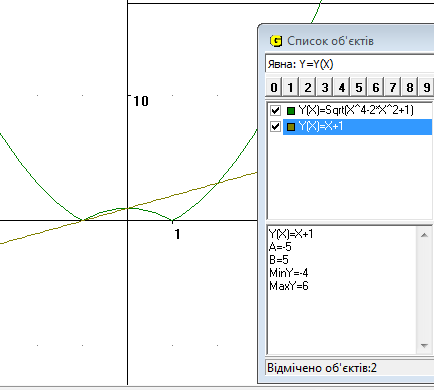
Рис.12
10. Побудувати графік функції 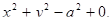
Для цього задаємо тип функції «неявна», а – задаємо як Р1. Змінюючи значення параметру за допомогою повзунку або вводячи значення Р1 з клавіатури ми бачимо як змінюється радіус кола (Рис.13.1). Якщо значення Р1 більше нуль або дорівнює 0, то порушується умова (Рис.13.2).
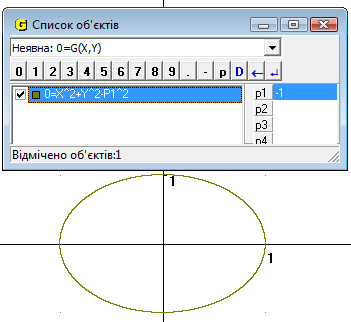
Рис.13.1
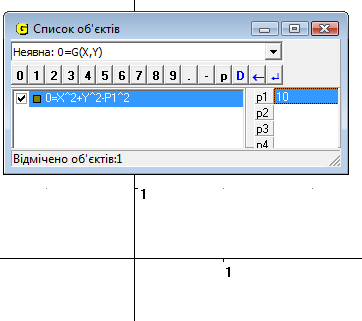
Рис.13.2
11. Побудувати графік функції 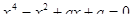
При початкових значеннях Р1=0 та Р2=0 ми отримуємо симетричну відносно вісі Оу фігуру, яка проходить черех початок координат (Рис.14.1). Якщо змінювати параметр Р1 (не змінюючи Р2) то ми бачимо як порушується симетрія, а функція все одно проходить через початок координат (Рис.14.2). Якщо змінювати параметр Р2 (не змінюючи Р1) ми бачимо, що симетрія не порушується, але відбуваеться ковзання графіку вздовж осі Оу (Рис.14.3). Якщо змінювати обидва параметри Р1 та Р2, то порушується і симетрія, і відбувається рух вздовж осі Оу.
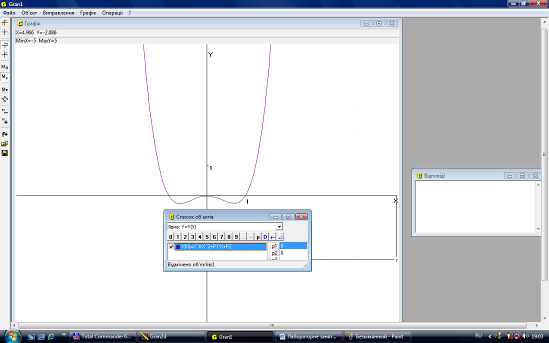
Рис.14.1
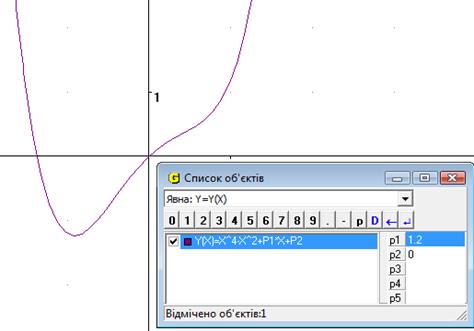
Рис.14.2
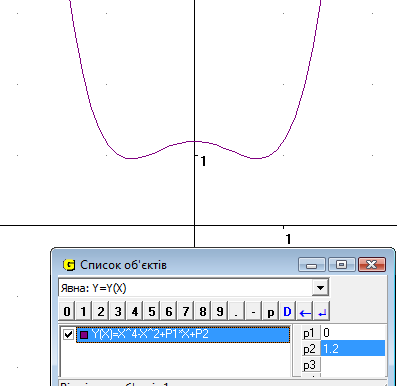
Рис.14.3
12. Побудувати графік функції 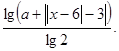
Якщо надати початкове значення Р1 = 0, то ми отримуємо розривну функцію (Рис.15.1). Якщо збільшувати значення параметра, то бачимо, що функція не має точок розриву, а при великому збільшенні Р1 не перетинає вісь Ох і піднімається вздовж Оу (Рис.15.2). Якщо ж навпаки зменшувати значення Р1, ми бачимо, що графік губить одну свою частину і рухається у ІІІ чтверть (Рис.15.3).
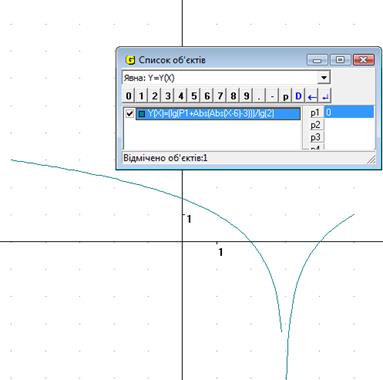
Рис.15.1
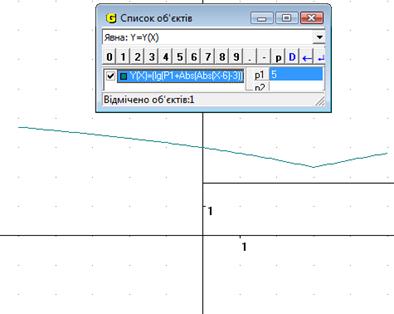
Рис.15.2
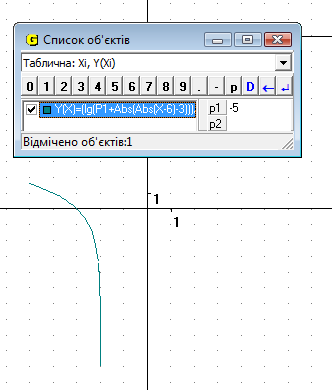
Рис.15.3
13. Побудувати графік функції 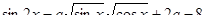
При початкових значеннях Р1 та Р2 ми бачимо, що графік функції складається з 2х частин і знаходиться у нижній частині сітки координат. При зміні Р1 відбувається зміна графіка (випуклість або вогнутість) (Рис.16.1), при зміні Р2 відбувається рух вздовж осі Оу (Рис.16.2). При зміні обох параметрів відбувається і рух вздовж осі ОУ, і зміна графіку (Рис.16.3).
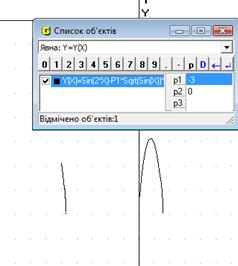
Рис.16.1
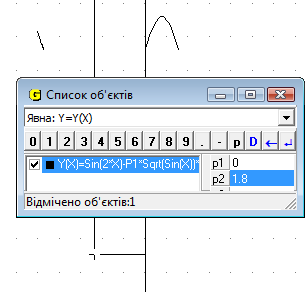
Рис.16.2
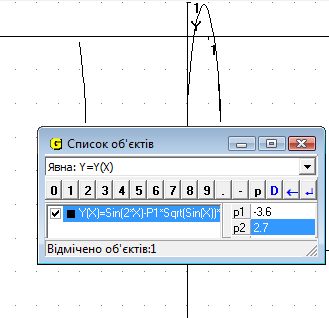
Рис.16.3
14. Вкажіть, скільки дійсних коренів має рівняння 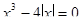 .
.
Виконавши найпростіші рівносильні перетворення, маємо рівняння 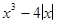 будуємо у ППЗ «GRAN1» графіки функцій
будуємо у ППЗ «GRAN1» графіки функцій 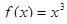 та
та 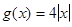 бачимо, що вони перетинаються лише у двох точках (x = 0; x = 2) і робимо висновок, що рівняння має два корені.
бачимо, що вони перетинаються лише у двох точках (x = 0; x = 2) і робимо висновок, що рівняння має два корені.
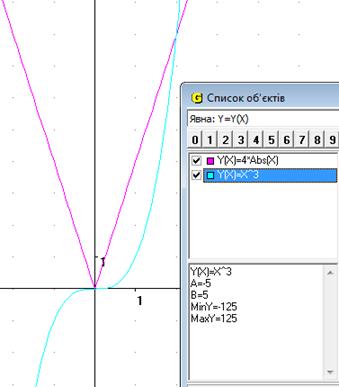
Рис.17
15. При яких значеннях параметра а нерівність 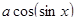 <0.
<0.
Треба побудувати графік функції f ( x) = а cos(sinx) та, змінюючя значення параметра а, з’ясувати, при яких значеннях параметру графік функції f(x) лежить вище осі Ох.
Будуємо у ППЗ «GRAN1» графік функції f (x) = а cos(sinx) і аналізують поведінку графіка цієї функції в залежності від значення параметра а.
Висновок. Нерівність має розв’язки при а < 0.
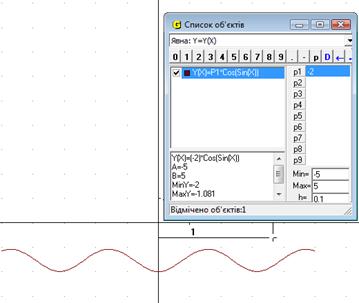
Рис.18.1
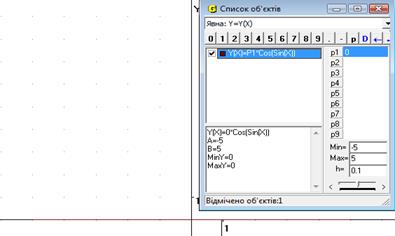
Рис.18.2
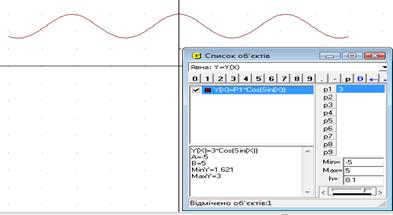
Рис.18.3
16. Обчислити інтеграл 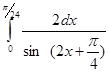 .
.
Спочатку створюємо функцію, малюємо графік. Тепер вибираємо вкладку Обчислення – Інтеграл.Отже значення інтеграла І=0.33 од (Рис.19).
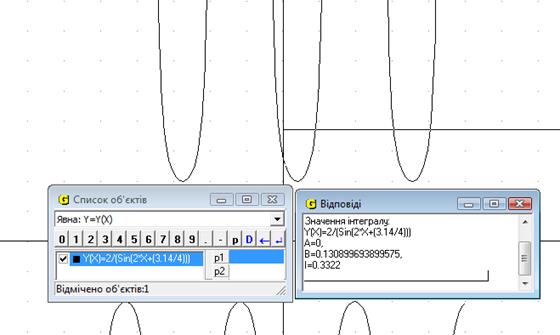
Рис.19
17. Обчислити інтеграл 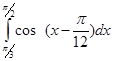 .
.
Як і в попередньому прикладі створюємо функцію та обчислюємо інтеграл. Відповідь: 0.26
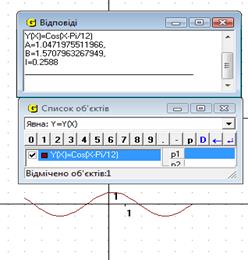
Рис.20
18. Обчислити інтеграл 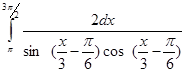 .
.
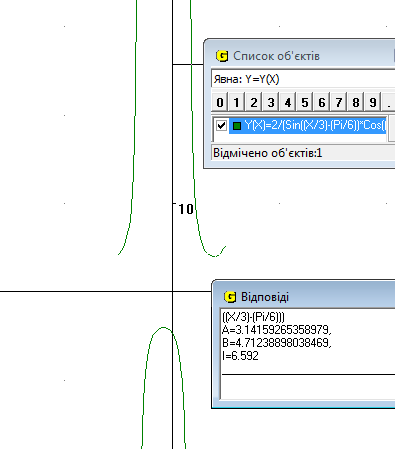
Рис.21
Відповідь: І=6.53 од (Рис.21).
19. Обчислити інтеграл 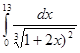
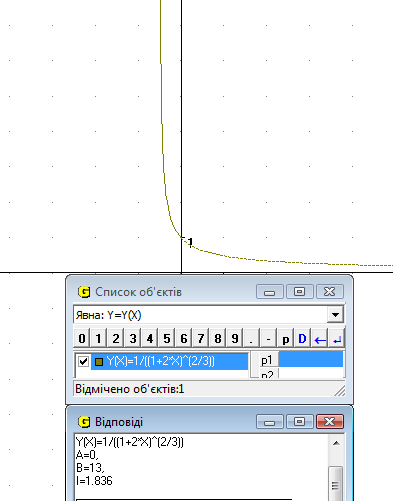
Рис.22
Відповідь: І=1.84 од (Рис.22).
20. Обчислити інтеграл 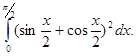
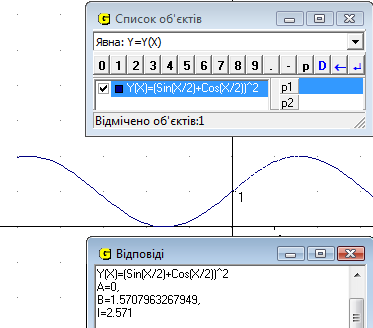
Рис.23
Відповідь: І=2.57 од (Рис.23).
Лабораторне заняття № 2
З курсу «Застосування ІКТ у навчанні математики»
Тема. Педагогічний програмний засіб GRAN 2
Навчально-матеріальне забезпечення. Персональні комп’ютери, програмне забезпечення Windows XP, ППЗ GRAN2.
Мета роботи. Отримати навички роботи з педагогічним програмним засобом GRAN2.
Завдання:
4. Виконати завдання.
5. Зберегти електронну версію отриманих результати.
6. Оформити звіт.
Звіт містить такі розділи:
- Титульний аркуш.
- Завдання роботи.
- Письмовий опис дій по виконанню завдань.
- Отримані результати.
Для роботи у програмі нам знадобляться деякі відомості.
Активні кнопки для швидкого створення об’єктів:
 створити точку
створити точку
 створити відрізок
створити відрізок
 створити промінь
створити промінь
 створити пряму
створити пряму
 створити коло
створити коло
 створити коло за радіусом
створити коло за радіусом
 створення середньої точки
створення середньої точки
 створення точки перетину об’єктів
створення точки перетину об’єктів
 створення паралельної прямої
створення паралельної прямої
 створення перпендикулярної прямої
створення перпендикулярної прямої
 створення ламаної
створення ламаної
також це можна зробити за допомогою вкладки «Створити».
Обчислення проводимо за допомогою вкладки «Обчислення».
Для створення динамічного виразу користуємося наступними:
LEN - довжина між двома точками, точкою і прямою, відрізка, кола, дуги, ламаної;
AREA - площа многокутника, кола, дуги, ламаної;
ANGLE - величина кута між трьома точками;
OANGLE - орієнтований кут між трьома точками;
XANGLE – кут нахилу вектора з віссю ОХ;
NORM – відстань від точки до початку координат;
ARG – полярний кут точки;
X – визначити координату точки Х;
Y – визначити координату точки Y.
Практичні завдання
1. Покажіть, що сума кутів трикутника дорівнює 180°.
2. З одної точки проведено дві дотичні до кола. Покажіть, що відрізки дотичних рівні.
3. На стороні АВ трикутника АВС взяли точку D. Покажіть, що відрізок CD менше принаймні однієї з сторін АС або ВС.
4. Два кола із центрами А і С перетинаються у двох точках E i F. Покажіть, що пряма АС перпендикулярна EF.
5. Покажіть, що серединні перпендикуляри до двох сторін трикутника перетинаються.
6. Покажіть, що у будь якому трикутнику всяка сторона менша за півпериметр.
7. Покажіть, що в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів (теорема Піфагора)
8. Покажіть, що центр кола вписаного у трикутник, є точкою перетину його бісектрис.
9. Знайти значення похідної від функції 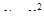 в точці
в точці 
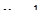 .
.
10. Знайти значення похідної від функції 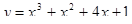 в точці
в точці 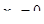 .
.
11. Тіло рухається зі швидкістю, яка змінюється за законом 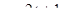 (м/с). Знайдіть шлях, який пройшло тіло за інтервал часу від t
(м/с). Знайдіть шлях, який пройшло тіло за інтервал часу від t 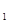 =1с до
=1с до  =3с.
=3с.
12. Обчислити роботу, яку треба виконати, щоб викачати воду з ями глибиною 4м., що має квадратний переріз зі стороною 2м. густина 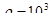 кг/м
кг/м 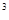 .
.
13. Знайти масу стержня завдовжки 35 см., якщо його лінійна густина змінюється за законом 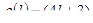 (кг/м).
(кг/м).
14. Знайти кількість електрики, що проходить через поперечний переріз провідника за 10с., якщо сила струму змінюється за законом 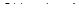 (А).
(А).
15. Експериментально встановлено, що продуктивність праці робітника наближено виражається формулою 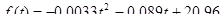 , де t - робочий час у годинах. Обчислити обсяг випуску за квартал, вважаючи робочий день восьмигодинним, а кількість робочих днів у кварталі – 62.
, де t - робочий час у годинах. Обчислити обсяг випуску за квартал, вважаючи робочий день восьмигодинним, а кількість робочих днів у кварталі – 62.
16. Експериментально встановлено, що залежність витрати бензину автомобілем від швидкості на 100 км шляху визначається формулою 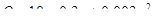 , де 30≤v≤110. Визначити середню витрату бензину, якщо швидкість руху 50 – 60 км/год.
, де 30≤v≤110. Визначити середню витрату бензину, якщо швидкість руху 50 – 60 км/год.
Розв’язання вправ
1. Покажіть, що сума кутів трикутника дорівнює 180° (Рис.24).
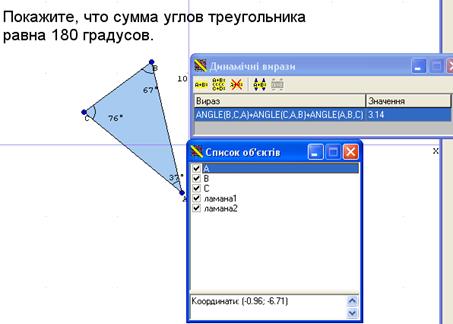
Рис.24
Створивши трикутник виміряємо кути за допомогою функції ANGLE. Для того щоб отримати суму кутів трикутника створимо динамічний вираз, у якому порахуємо суму кутів нашого трикутника. Отримане число π (180°). Тепер за допомогою мишки можемо змінювати координати будь якої вершини трикутника, тобто змінюючи величину кута. Але все рівно бачимо у вікні «Динамічні вирази» бачимо, що сума дорівнює π.
2. З одної точки проведено дві дотичні до кола. Покажіть, що відрізки дотичних рівні.
3.
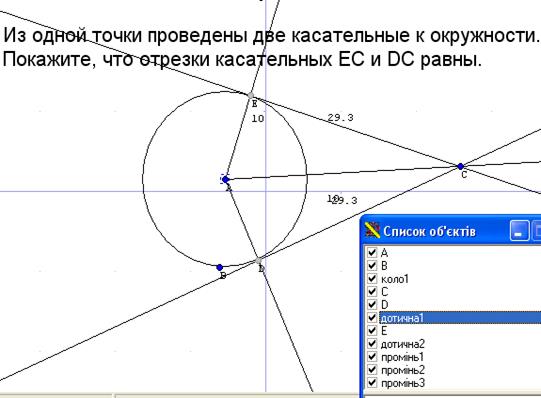
Рис.25
Створюємо коло. Створюємо точку, яка не належить площині кола.
Створюємо дотичні до кола EC, DC. Вимірюємо довжини дотичних за допомогою Обчислення – Відстань. Тепер змінюючи положення центру кола, радіусу кола або положення точки С ми бачимо, що довжини дотичних рівні (Рис.25).
4. На стороні АВ трикутника АВС взяли точку D. Покажіть, що відрізок CD менше принаймні однієї з сторін АС або ВС.
Створюємо трикутник. Створюємо точку, яку прикріпляємо до будь якої з сторін трикутника. Через цю точку і протилежну вершину створюємо відрізок. Тепер у «динамічний вираз» обчислимо довжини сторін які нас цікавлять, та довжину відрізку. Довжину вимірюємо за допомогою функції LEN.
Змінюючи положення вершин, або точки Dпереконуємось у тому, що відрізок CD менше принаймні однієї з сторін АС або ВС (рис.26).
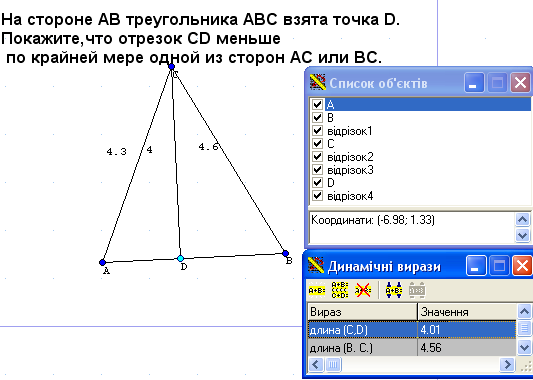
Рис.26
7. Два кола із центрами А і С перетинаються у двох точках E i F. Покажіть, що пряма АС перпендикулярна EF.
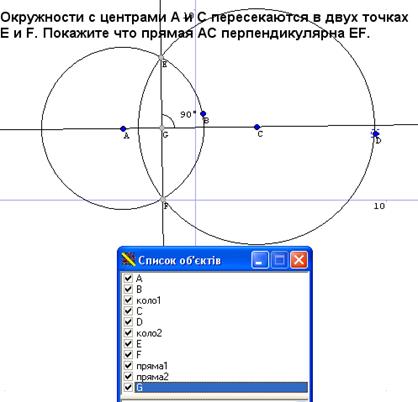
Рис.27
Створюємо 2 кола. Через їх центри проводимо пряму. Створюємо 2 точки перетину кіл (прикріпляємо їх до перетину 2х об’єктів). Через ці точки проводимо пряму. Створюємо точку перетину прямих. Тепер вимірюємо кут між цими прямими Обчислення – кут.
Тепер змінюючи положення центрів кола, або радіус ми бачимо що пряма АС перпендикулярна EF (Рис.27).
Якщо кола не перетинаються, то умова задачі не зберігається.
8. Покажіть, що серединні перпендикуляри до двох сторін трикутника перетинаються.
Створюємо трикутник. Створюємо середню точку на 2х сторонах Об’єкт – Створення – Середня точка.
Створюємо перпендикуляри до середніх точок.
Тепер змінюючи положення вершин ми бачимо, що серединні перпендикуляри перетинаються або в площині трикутника, або поза нею (Рис.28).
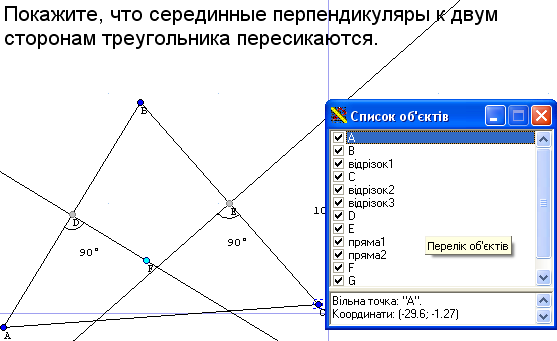
Рис.28
9. Покажіть, що у будь якому трикутнику всяка сторона менша за півпериметр.
Створюємо трикутник. Вимірюємо довжини сторін. У динамічному виразі створюємо формулу півпериметра для нашого трикутника.
Тепер змінюючи вершини трикутника бачимо, що всяка сторона менша за півпериметр (Рис.29).
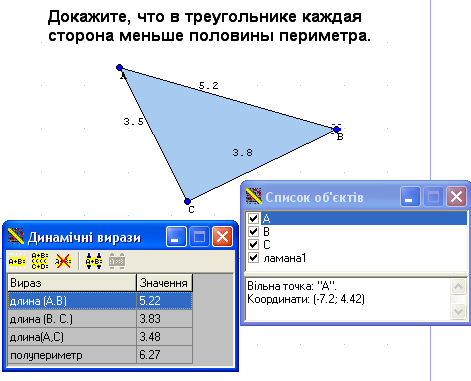
Рис.29
10. Покажіть, що в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів (теорема Піфагора)
Створюємо прямокутний трикутник. У динамічний вираз вводимо необхідні нам вирази – квадрат гіпотенузи та сума квадратів катетів.
Тепер при зміні положень вершин трикутника ми бачимо як змінюються наші числові вирази, але все рівно ми бачимо що виконується рівність Піфагора, що в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів (Рис.30).
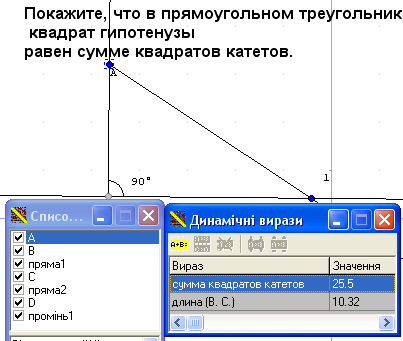
Рис.30
11. Покажіть, що центр кола вписаного у трикутник, є точкою перетину його бісектрис.
Створюємо трикутник. Створюємо бісектриси вершин трикутника Об’єкт – Створення – Бісектриса кута. Створюємо точку перетину бісектрис. Створюємо коло, вписане у трикутник. Тепер змінюючи вершини трикутника, ми бачимо що змінюються положення бісектрис, але все рівно центр кола вписаного у трикутник, є точкою перетину його бісектрис (Рис.31).
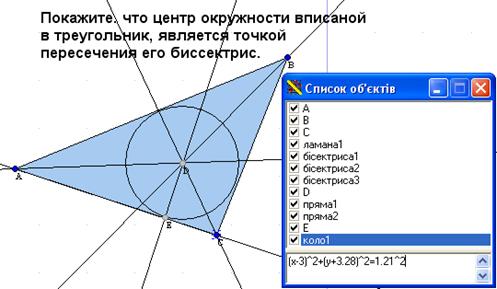
Рис.31
12. Знайти значення похідної від функції  в точці
в точці 
 .
.
Для цього створимо функціональну залежність. Тепер у вкладці Обчислення вибираємо Похідна.
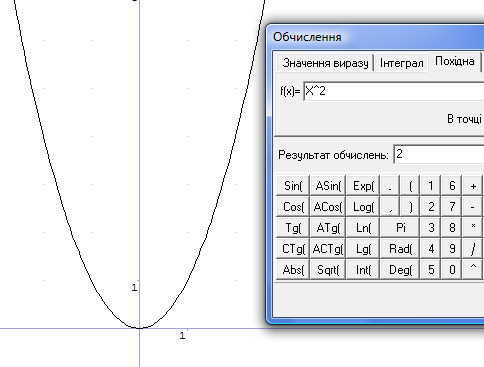
Рис.32
Відповідь: значення похідної від функції  в точці
в точці 

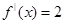 .
.
13. Знайти значення похідної від функції 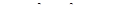 в точці
в точці 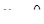 .
.
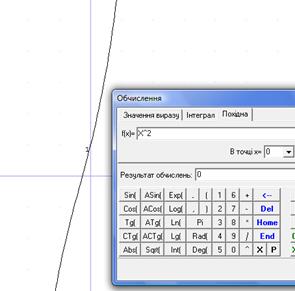
Рис.33
Відповідь: значення похідної від функції 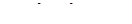 в точці
в точці 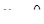
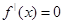 .
.
14. Тіло рухається зі швидкістю, яка змінюється за законом 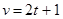 (м/с). Знайдіть шлях, який пройшло тіло за інтервал часу від t
(м/с). Знайдіть шлях, який пройшло тіло за інтервал часу від t 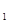 =1с до
=1с до 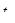 =3с.
=3с.
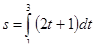
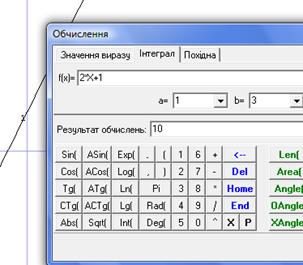
Рис.35
Отже, пройдений шлях дорівнює 10 м.
15. Обчислити роботу, яку треба виконати, щоб викачати воду з ями глибиною 4м., що має квадратний переріз зі стороною 2м. густина 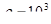 кг/м
кг/м 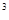 .
.
Значення сили F(x), що діє на переріз прямокутного паралелепіпеда площею 4м 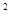 , визначають вагою шару води, що знаходиться вище від цього перерізу. Отже,
, визначають вагою шару води, що знаходиться вище від цього перерізу. Отже, 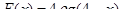 , де х
, де х 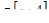 , g
, g 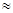 9,8.
9,8.
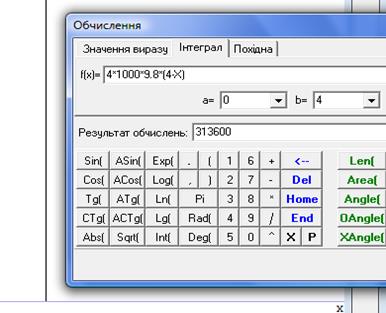
Рис.36
Отже, А= 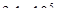 Дж.
Дж.
16. Знайти масу стержня завдовжки 35 см., якщо його лінійна густина змінюється за законом 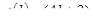 (кг/м).
(кг/м).
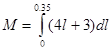
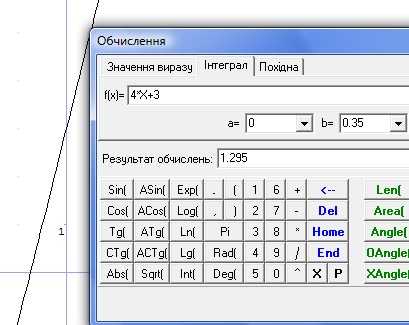
Рис.37
Маса стержня дорівнює 1.3 кг.
17. Знайти кількість електрики, що проходить через поперечний переріз провідника за 10с., якщо сила струму змінюється за законом 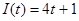 (А).
(А).
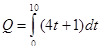
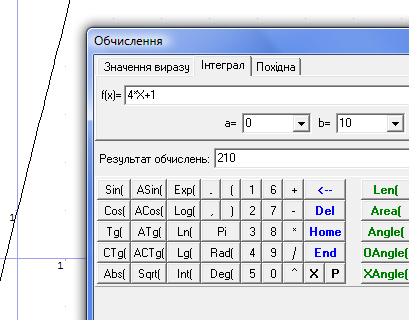
Рис.38
Відповідь: 210 Кл.
18. Експериментально встановлено, що продуктивність праці робітника наближено виражається формулою 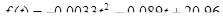 , де t - робочий час у годинах. Обчислити обсяг випуску за квартал, вважаючи робочий день восьмигодинним, а кількість робочих днів у кварталі – 62.
, де t - робочий час у годинах. Обчислити обсяг випуску за квартал, вважаючи робочий день восьмигодинним, а кількість робочих днів у кварталі – 62.
Обсяг випуску продукції протягом зміни є первісною від функції, що виражає продуктивність парці. Тому 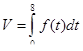 . Протягом кварталу обсяг випуску продукції становитиме
. Протягом кварталу обсяг випуску продукції становитиме 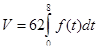 .
.
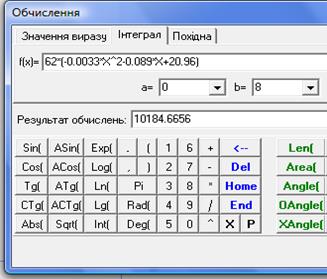
Рис.39
Отже, обсяг випуску за квартал становитиме 10185 (од).
19. Експериментально встановлено, що залежність витрати бензину автомобілем від швидкості на 100 км шляху визначається формулою  , де 30≤v≤110. Визначити середню витрату бензину, якщо швидкість руху 50 – 60 км/год.
, де 30≤v≤110. Визначити середню витрату бензину, якщо швидкість руху 50 – 60 км/год.
Середня витрата бензину становить 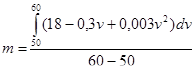
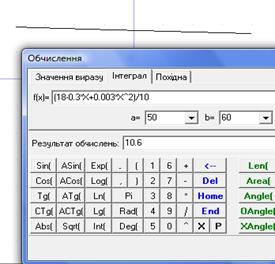
Рис.40
Автомобіль на 100 км шляху, рухаючись зі швидкістю 50 -60 км/год. Витрачає в середньому 10.6л.
Лабораторне заняття №1
З курсу «Застосування ІКТ у навчанні математики»
Тема. Педагогічний програмний засіб GRAN 3
Навчально-матеріальне забезпечення. Персональні комп’ютери, програмне забезпечення Windows XP, ППЗ GRAN 3.
Мета роботи. Отримати навички роботи з педагогічним програмним засобом GRAN 3.
Завдання:
1. Виконати завдання.
2. Зберегти електронну версію отриманих результати.
3. Оформити звіт.
Звіт містить такі розділи:
· Титульний аркуш.
· Завдання роботи.
· Письмовий опис дій по виконанню завдань.
· Отримані результати.
Для роботи у програмі нам знадобляться деякі відомості.
 створити точку
створити точку
 створити ламану
створити ламану
 створити площину
створити площину
 створити многогранник
створити многогранник
 створити поверхню
створити поверхню
 створити поверхню обертання
створити поверхню обертання
Також об’єкт можна створити за допомогою вкладки Об’єкт – Створити.
Обчислення робимо за допомогою вкладки Обчислення.
Практичні завдання
1. Створити призму та виконати її переріз. Виконати наступні операції над об’єктом: паралельне, перенесення поворот, деформація. Обчислити площі та периметри граней. Обчислити відстані між вершинами, ребрами, площинами.
2. Створити піраміду та виконати її переріз. Обчислити кути бокових граней. Обчисліть кути між площиною переізу і площиною піраміди.
3. Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Ох функції  та прямими у= 0 та х=3.
та прямими у= 0 та х=3.
4. Знайти об’єм тіла, утвореного обертанням навколо осі Ох функції 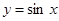 і прямими у = 0, х = 0, х =
і прямими у = 0, х = 0, х = 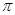
5. Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Ох функції 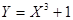 , у = 0, х = 2, х= 1.
, у = 0, х = 2, х= 1.
6. Знайти площу повної поверхні тіла, утвореного обертанням навколо осі Ох функції  у = 0, х = 0 , х =
у = 0, х = 0 , х = 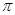 /2.
/2.
Розв’язання вправ
1. Для цього викриваємо вкладку Об’єкт – створити базовий об’єкт – вибираємо призма. Тепер створимо переріз. Тип об’єкту площина. Обираємо 3 точки на ребрах або обираємо точки вершини призми. Через три точки можна провести площино. Отримуємо наш переріз. Наступні обчислення виконуємо за допомогою вкладки Обчислення.
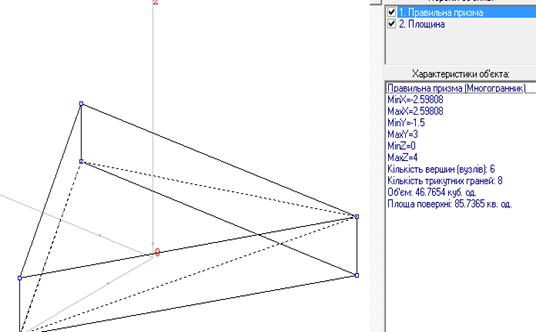
Рис.41
2. Для цього викриваємо вкладку Об’єкт – створити базовий об’єкт – вибираємо піраміда. Тепер створимо переріз. Тип об’єкту площина. Обираємо 3 точки на ребрах або обираємо точки вершини піраміди. Через три точки можна провести площино. Отримуємо наш переріз. Наступні обчислення виконуємо за допомогою вкладки Обчислення.
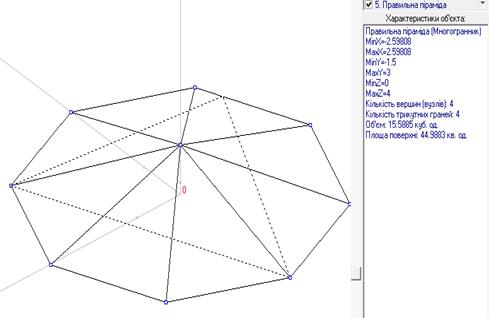
Рис.42
3. Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Ох функції  та прямими у= 0 та х=3.
та прямими у= 0 та х=3.
Спочатку створюємо поверхню обертання. Для цього : Об’єкт – поверхня обертання - вибираємо тип залежності, навколо якої вісі обертаємо, вибираємо початкове і конечне значення Х.
Натискаємо кнопку Виконати.
У робочому вікні програми отримуємо нашу поверхню. За допомогою повзунків можемо роздивитись нашу поверхню.
У вікні Характеристики об’єкта отримуємо відповіді. Ці відповіді можемо порівняти із відповідями отриманими у лабораторній роботі №1.

Рис.43
4. Знайти об’єм тіла, утвореного обертанням навколо осі Ох функції 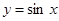 і прямими у = 0, х = 0, х =
і прямими у = 0, х = 0, х = 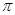
Створення об’єкта як у попередньому випадку.

Рис.44
Порівняйте отриману відповідь із відповіддю отриманою у лабораторній роботі №1.
5. Знайти об’єм тіла та площу повної поверхні тіла, утвореного обертанням навколо осі Ох функції 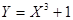 , у = 0, х = 2, х= 1.
, у = 0, х = 2, х= 1.
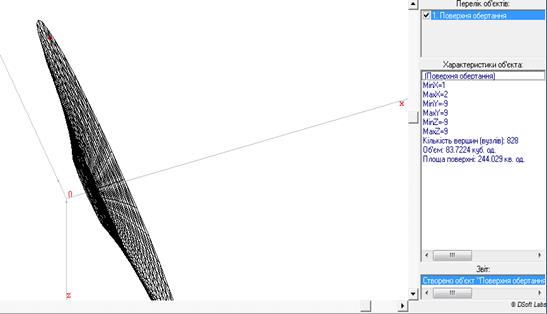
Рис.45
Порівняйте отриману відповідь із відповіддю отриманою у лабораторній роботі №1.
6. Знайти площу повної поверхні тіла, утвореного обертанням навколо осі Ох функції 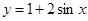 у = 0, х = 0 , х =
у = 0, х = 0 , х = 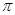 /2.
/2.

Рис.46
ВИСНОВКИ ДО ДРУГОГО РОЗДІЛУ
Метою вивчення навчальної дисципліни «Застосування інформаційно-комунікаційних технологій у процесі навчання математики» є формування у студентів інформаційної та методологічної компетентностей майбутніх вчителів математики.
В основу навчального процесу, організованого з використанням ІКТ, повинні бути покладені загально визнані дидактичні принципи навчання.Такі як:
- Принцип науковості.
- Принцип наочності.
- Принцип систематичності та послідовності.
- Принцип активного залучення учнів до навчального процесу.
- Принцип індивідуалізації, індивідуального підходу у навчанні.
- Принцип доступності.
ПЗНП повинні відповідати вимогам педагогічної доцільності та виправданості їх застосування, які полягають у тому, що програмний засіб слід наповнювати таким змістом, який найбільш ефективно може бути засвоєний тільки за допомогою комп’ютера, і використовувати тільки тоді, коли це дає незаперечний педагогічний ефект.
Тип програмного засобу з точки зору його місця у навчальному процесі може бути визначений відповідно до поданої нижче класифікації.
1. Демонстраційно-моделюючі програмні засоби.
2. Педагогічні програмні засоби типу діяльнісного предметно-орієнтованого середовища.
3. Педагогічні програмні засоби, призначені для визначення рівня навчальних досягнень.
4. Педагогічні програмні засоби довідково-інформаційного призначення.
Можливість проведення комп’ютерних експериментів у середовищі СКМ дає змогу організувати навчання математики з використанням елементів проблемного навчання, дослідницьких підходів у навчанні.
Головною умовою застосування СКМ у процесі навчання математики є те, що воно завжди має бути педагогічно доцільним і виваженим, здійснюватися з метою досягнення поставленої навчальної мети уроку, шляхом встановлення міжпредметних зв’язків курсів математики та інформатики у формі інтегрованих уроків.
У другому розділі ми навели розробки лабораторних занять для Змістовного модуля 4. «Програмні засоби у навчанні математики». Розробили практичні завдання, які можна розв’язувати у програмних засобах GRAN1, GRAN-2D, GRAN-3D. У кожній лабораторній роботі присутній необхідний теоретичний мінімум для роботі у програмі. Далі наведені практичні завдання. Також ми показали яким чином розв’язувати наведені вправи у цих програмах. Наведені малюнки наочно демонструють розв’язані вправи.
Висновки
Проблема формування готовності студентів до майбутньої професійної діяльності, акумулює проблеми психологічної науки, пов'язані із особливостями особистості, рисами її характеристики, потенційними можливостями, які обумовлюють успішність професійної підготовки. Психологія формування готовності до професійної діяльності вивчалася українськими дослідниками, серед яких: Г.О. Балл, Г.С. Костюк, Є.О. Мілерян, В.О. Моляко, П.С. Перепелиця, М.Л. Смульсон та ін. Готовність розглядається науковцями в безпосередньому зв'язку з формуванням, розвитком і вдосконаленням психічних процесів, станів, якостей особистості, необхідних для успішної діяльності.
У процесі розробки моделі формування готовності майбутніх вчителів математики до застосування ІКТ, можна виокремити певні етапи.
1. Детальне дослідження, аналіз та обговорення проблеми інформатично-комунікативних компетентностей майбутнього вчителя математики.
2. Планування організаційно-методичних заходів, спрямованих на близьку та далеку перспективи, особистісну мотивацію студентів.
3. Впровадження інформатично-комунікативних компетентностей у зміст навчання ІКТ майбутніх вчителів.
4. Оцінювання готовності майбутніх вчителів до застосування ІКТ у процесі навчання ІМ.
Навчальний курс “Інформаційно-комунікаційні технології в освіті” призначений для студентів вищих педагогічних навчальних закладів, спеціальність “Математика”.
Головним завданням вивчення навчальної дисципліни є підготовка майбутніх викладачів математики до практичного використання в своїй діяльності сучасних засобів і технологій, формування у них інформаційної культури.
Наша робота складається з двох розділів. У першому розділі ми проаналізували стан досліджуваної проблеми, виявили можливості вдосконалення методичної системи навчання математики в педагогічному ВНЗ за рахунок широкого впровадження засобів ІКТ у навчальний процес.
У другому розділі ми розглянули класифікацію математичних пакетів та ППЗ. Також ми виконали розробки для комп’ютерної підтримки навчально – пізнавальної діяльності студентів при навчанні математики, розробили плани – конспекти лабораторних занять.
Таким чином, підводячи підсумки роботи, ми можемо стверджувати, що ми виконали поставлену на початку мету даної курсової роботи – розробили методичні рекомендації проведення лабораторних занять з курсу “Застосування ІКТ в процесі навчання математики».
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1. Апатова Н. П. Інформаційні технології в навчанні математики // Сучасні інформаційні технології в навчальному процесі. – К.:НПУ, 1997. – С. 39.
2. Апатова Н.В. Влияние информационных технологий на содержание и методы обучения в СЗШ: дис. ... д-ра пед. наук: 13.00.01 / Н.В. Апатова. - К., 1999. - 342 с.
3. Барышкин А.Г. Компьютерные презентации на уроке математики / А.Г. Барышкин, Т.В. Шубина, Н.А. Резник // Компьютерные инструменты в образовании. - 2005. - № 1. - С.62 - 70.
4. Батышев С.Я. Профессиональная педагогика: Учебник для студентов, обучающихся по педагогическим специальностям и направлениям. – 2 е изд., перераб. и доп. / С.Я. Батышев. – М.: Ассоциация «Профессиональное образование», 1999. – 904 с.
5. Бешанов С.А. Информатизация и информационные процессы / С.А. Бешанов, Лыскова В.Ю. – Омск, 1999. – 144 с.
6. Вербицький А.А. Формування пізнавальної та професійної мотивації. – М.: Освіта, 1986. – 364 с.
7. Державна програма «Інформаційні та комунікаційні технології в освіті і науці» на 2006-2010 рр. [Електронний ресурс] // Режим доступу: http://www.mon.gov.ua/laws/KMU_1153.doc.
8. Жалдак М. І., Вітюк О. В. Комп’ютер на уроках геометрії: Посіб. для вчителів. - К.: Дініт, 2002. – 170 с.
9. Жалдак М.І. Комп’ютер на уроках геометрії: Посібник для вчителів / М.І. Жалдак, О.В. Вітюк– К.: РННЦ „ДІНІТ”, 2003. – 168 с.
10. Жалдак М.І. Комп’ютерно-орієнтовані засоби навчання математики, фізики, інформатики: [посібник для вчителів] / М.І. Жалдак, В.В. Лапінський, М.І. Шут − К.: Дініт, 2004. − 110 с.
11. Жалдак М.І. Педагогічний потенціал комп’ютерно-орієнтованих систем навчання математики / М.І. Жалдак // Комп’ютерно-орієнтовані системи навчання: зб. наук. праць / Редкол. – К.: НПУ ім. М.П.Драгоманова. –[Вип. 7]. – 2003. – С. 3-16.
12. Жуков Г.Н Основы общей и профессиональной педагогики: Учебное пособие / Под общ ред проф Г.П. Скамницкой. – М.: Гардарики, 2005. – 382 с.
13. Інноваційні інформаційно-комунікаційні технології навчання математики: навчальний посібник / В.В. Корольський, Т.Г. Крамаренко, С.О. Семеріков, С.В. Шокалюк; науковий редактор академік АПН України, д.пед.н., проф. М.І. Жалдак. – Кривий Ріг: Книжкове видавництво Кирєєвського, 2009. – 316 с.
14. Колеченко І.В. Енциклопедія педагогічних технологій; посібник для викладачів. – СПб.:КАРО, 2005. – 368 с.
15. Крамаренко Т.Г. Уроки математики з комп’ютером: [посіб. для вчителів і студ.] / Т.Г. Крамаренко; за ред. М.І. Жалдака. − Кривий Ріг: Видавничий дім. − 2008. − 272 с.
16. Кругликов Г.И. Методика профессионального обучения с практикумом.
17. Мадзігон В.М. Педагогічні аспекти створення і використання електронних засобів навчання / В.М. Мадзігон, В.В. Лапінський, Ю.О. Дорошенко // Проблеми сучасного підручника: Зб. наук. праць / Редкол. – К.: Педагогічна думка, 2003. – Вип. 4. – С. 70–81.
18. Машбиц Е.И. Психолого-педагогические проблемы компьютеризации обучения / Е.И. Машбиц. – М.: Педагогика, 1988.
19. Морзе Н. В. Основи інформаційно-комунікаційних технологій / Наталія Вікторівна Морзе. – К.: Видавнича група BHV, 2006. – 352 с.
20. Никишина І.В. Інноваційна діяльність сучасного педагога: методичний посібник. – Вчитель, 2007. – 91 с.
21. Пеньков А. В. Использование новой информационной технологии при преподавании математики в старших классах средней школы. Дис. … канд. пед. наук: 13.00.02 / А. В. Пеньков. – К.: КДПУ ім. М. П. Драгоманова, 1992. – 172 с.
22. Підготовка учнів до професійного навчання і праці (психолого-педагогічні основи): Навч. посібник / Під ред. Г.О. Балла, П.С. Перепелиці, В.В. Рибалки. – К.: Наукова думка, 2000. – 188 с.
23. Пінчук О.П. Використання педагогічних програмних засобів на уроках математики. // Математика в школах України. №19-20.-2006.-С.34.
24. Пічуріна А.Ф. Виховання учнів на уроках математики. – М.: Освіта, 1987. – 390 с.
25. Погорєлов О.В. Геометрія, 10 – 11. – Київ: Освіта, 1995. – 141 с.
26. Погорєлов О.В. Геометрія: Підручник для 7-11 класів середньої школи. – К.: Радянська школа, 1992. – 352 с.
27. Раков С. А. Програмно-методичний комплекс DG як крок від традиційної до інформаційної технології навчання геометрії/ С. А. Раков, В. П. Горох. // Комп’ютер у школі і сім’ї. – 2003. – № 1. – С. 20-23.
28. Раков С.А. Відкриття геометрії через комп'ютерні експерименти в пакеті DG / С.А. Раков, В.П. Горох, К.О. Осенков, О.В. Думчикова, О.В. Костіна, О.Р. Ларін, В.Т. Лисиця, В.В. Пікалова. -Харків: ХДПУ, 2002. - 108 с
29. Раков С.А. Математична освіта: компетентнісний підхід з використанням ІКТ: Монография / С.А. Раков. - Х.:Факт, 2005. - 360 с
30. Раков С.А. Пакет DG та дослідницький підхід у курсі алгебри та початків аналізу ЗНЗ / С.А. Раков // Комп'ютер у школі і сім'ї. - 2005. -№7.- С13-17.
31. Рамський Ю. С. Формування інформаційної культури особи – пріоритетне завдання сучасної освітньої діяльності / Юрій Савіянович Рамський // Науковий часопис НПУ імені М. П. Драгоманова. – Серія №2. – Комп’ютерно-орієнтовані системи навчання: Збірник наукових праць / Редрада. – К.: НПУ імені М. П. Драгоманова, 2004. – № 1 (8). – С. 19-42.
32. Рамський Ю.С. Про роль математики та деякі тенденції розвитку математичної освіти в інформаційному суспільстві / Ю.С. Рамський // Математика в школі. – 2007, № 7. – С. 36 – 40.
33. Рафальська М.В. Інтегровані уроки з математики та інформатики з використанням систем комп’ютерної математики// Комп’ютер у школі та сім’ї.– 2008 – №8 (72).– С.27-30.
34. Роберт И.В. Современные ИТ технологии в образовании: дидактические проблемы, перспективы использования / И.В. Роберт. – М.: Школа-Пресс, 1994. – 178 с.
35. Робота з мультимедійною дошкою / упоряд. В. Латиський. -К.: Шк. світ, 2008. - 112 с. - (Бібліотека «Шкільного світу»).
36. С.А.Раков, В.П.Горох, К.О.Осенков, О.В.Думчикова, О.В.Костіна, О.Р.Ларін, В.Т.Лисиця, В.В.Пікалова.Відкриття геометрії через комп’ютерні експерименти в пакеті DG. – Харків: ХДПУ, – 2002. – 108 с.
37. Савченко О.Я. Новий зміст освіти в основній і старшій школі/ Савченко О.Я.// Матеріали міжнародної науково-практичної конференції "Інформаційно-комунікаційні технології у середній і вищій школі" (м. Ізмаїл, 27-29 травня 2004 р.). – Київ-Ізмаїл, 2004. – 236 с.
38. Скафа Е.И. Информационные технологии обучения и их роль в формировании эвристической деятельности учащихся / Е.И. Скафа // Дидактика математики: проблеми і дослідження. - 2003. - Вии. 19. - С.9-21.
39. Скафа О.І. Компютерно-орієнтовані уроки в еврестичному навчанні математики: навчально-методичний посібник / О.І. Скафа, О.В. Тутова. – Донецьк: вид-во “Вебер”, 2009. – 320 c.
40. Смирнов А.Н. Проблемы электронного учебника / А.Н. Смирнов // Математика в школе. - 2000. - №5. - С. 36-37.
41. Смолянникова О.Г. Мультимедиа в образовании. Теоретические основы и методика использования / О.Г. Смолянникова. – Красноярск.: Изд. КрасГУ, 2002.
42. Співаковський О.В. Теоретико-методичні основи навчання вищої математики майбутніх вчителів математики з використанням інформаційних технологій: автореф. ... д-ра пед. наук: 13.00.02 / О.В. Співаковський. -К., 2004-44 с
43. Триус Ю.В. Комп'ютерно-орієнтовані методичні системи навчання математики: Монографія / Ю.В. Триус. - Черкаси: Брама-Україна, 2005.-400 с
44. Тутова О.В. Методичні вимоги до організації процесу навчання математики на основі використання інформаційно-комунікаційних технологій / О.В. Тутова // Дидактика математики. - 2007. - № 27. - С.95 -101.
45. Шкіль М.І., Колесник Т.В., Хмара Т.М. Алгебра і початки аналізу: Підруч. для учнів 10 кл. з поглибл. вивч. математики в серед. закладах освіти. – К.: Освіта, 2000. – 318 с.
46. Шкіль М.І., Колесник Т.В., Хмара Т.М. Алгебра і початки аналізу: Підруч. для учнів 11 кл. з поглибл. вивч. математики в серед. закладах освіти. К.: Освіта, 2001. – 311 с.
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАІНИ
Бердянський державний педагогічний університет
фізико-математичний факультет
Кафедра математики,
методики викладання математики
Курсова робота
Методика проведення лабораторних занять з курсу
«Застосування ІКТ у навчальному процесі з математики»
Студентки 6 курсу
Заочної форми навчання
Васильєвої Інесси Сергіївни
Науковий керівник:
Ачкан В.В.
Бердянськ
2011
ЗМІСТ
РОЗДІЛ І
ТЕОРЕТИЧНІ ЗАСАДИ З КУРСУ «ЗАСТОСУВАННЯ ІКТ У ПРОЦЕСІ НАВЧАННЯ МАТЕМАТИКИ»
І.1 Роль та місце ІКТ при підготовці майбутніх вчителів математики
І.2 Лабораторні заняття як форма організації процесу навчання математики
І.3 Психолого—педагогічні основи вивчення курсу «Застосування ІКТ у процесі навчання математики»
ВИСНОВКИ РОЗДІЛУ І
РОЗДІЛ ІІ
КОМПОНЕНТИ МЕТОДИЧНОЇ СИСТЕМИ НАВЧАННЯ З КУРСУ «ЗАСТОСУВАННЯ ІКТ У ПРОЦЕСІ НАВЧАННЯ МАТЕМАТИКИ»
ІІ.1 Методичні вимоги щодо вибору навчальної програми з курсу «Застосування ІКТ у процесі навчання математики»
ІІ.2 Сучасні ППЗ та профільні математичні засоби у навчальному процесі
ІІ.3 Методична розробка лабораторних занять Змістовного модуля 4. «Програмні засоби у навчанні математики» з курсу «Застосування ІКТ у процесі навчання математики»
ВИСНОВКИ РОЗДІЛУ ІІ
ВИСНОВКИ
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
ВСТУП
Однією з основних задач як вищої, так і середньої школи сьогодні є підготовка школярів та студентів до життя в інформатизованому суспільстві. Інформаційну культуру потрібно розглядати як невід'ємну складову загальної культури та освіти фахівця. Під час формування інформаційного суспільства комп'ютер стає звичайним робочим інструментом фахівця будь–якої галузі діяльності.
Серед всіх навчальних дисциплін в педагогічному університеті особливе місце належить курсу математики. Вивчення курсу математики формує науковий світогляд, розуміння сутності прикладних проблем, дозволяє оволодіти методами математичного моделювання. У педагогічних ВНЗ особливої уваги потребує підготовка вчителя математики, тому що математика є одним із провідних предметів у системі шкільної і вузівської освіти.
Вимоги до математичної освіти на сучасному етапі зазнали деяких змін, а саме: зменшилася кількість годин, що відводилися на класичний аналіз, алгебру, геометрію. Вводяться нові навчальні дисципліни, поява яких продиктована практичною необхідністю прикладного застосування математики. Введення у навчальний процес цих дисциплін неможливе без застосування сучасних інформаційно–комунікаційних технологій (ІКТ), а головне — спеціалізованих математичних пакетів та програм навчального призначення.
Використання інформаційно-комунікаційних технологій має бути педагогiчно виправданим, розглядатись передусiм з точки зору педагогiчних переваг, якi воно може дати порiвняно з традицiйною методикою. Для успiшного застосування IКТ при вивченнi курсу математики в педагогічних університетах необхiдно внести певні змiни в методику навчання даного предмета. Програмна пiдтримка курсу математики повинна сприяти досягненню педагогiчних цілей за рахунок використання комп'ютерних засобiв для iлюстрацiї математичних понять, демонстрацiї застосувань математичних методiв дослiдження рiзноманiтних процесiв i явищ, проведення чисельного експерименту, створення та вивчення iнформацiйних i математичних моделей різноманітних явищ i процесiв, проведення комп'ютерних експериментів у геометрії.
Все ширше використовуються комп'ютери та чисельні методи для розв'язування прикладних задач. Вимоги чисельного розв'язування прикладних задач привели до появи великої кількості нових методів. Відбувається інтенсивне теоретичне переосмислення як традиційних, так і нових чисельних методів та їх систематизація.
Сьогодні вже накопичено значний досвід використання сучасних IКТ в навчальному процесі школи та ВНЗ, який висвітлено в працях Н.В.Апатової, Н.Р.Балик, В.Г.Болтянського, А.Ф.Верланя, О.М.Довгяло, А.П.Єршова, М.І.Жалдака, Л.В.Занкова, Т.Б.Захарова, О.А.Кузнєцова, В.І.Клочка, В.М.Монахова, Н.В.Морзе, С.А.Ракова, Ю.С.Рамського, В.Г.Розумовського, Ю.В.Триуса та інших.
При підготовці вчителя математики необхідно враховувати "специфічні закони, закономірності, принципи, особливості і умови освіти, навчання, виховання та формування особистості професіонала". Розглядаючи характер і зміст праці фахівців в умовах науково–інформаційного суспільства, потрібно враховувати засоби професійної діяльності фахівця. В умовах широкого використання засобів ІКТ такими інструментами виступають математичні пакети, що створювалися для фахівців–математиків. Математичні пакети можна використовувати і для навчання, тобто як педагогічні програмні засоби. Різні аспекти використання математичних пакетів як технічні, так і дидактичні розглядаються в працях таких вчених, як В.З.Аладьєв, М.Л.Шишаков, В.П.Дьяконов, Т.В.Капустіна, Ю.Ф.Лазарев, Б.М.Манзон, В.Ф.Очков, В.Г.Потьомкін та інших.
В Україні в напрямі інформатизованих систем навчання математики активно працює школа академіка АПН М.І.Жалдака – Є.Ф.Вінниченко, О.В.Вітюк, М.С.Головань, Ю.В.Горошко, Т.В.Зайцева, В.І.Клочко, І.В.Лупан, Г.О.Михалін , Н.В.Морзе, А.В.Пеньков, Ю.С.Рамський, О.А.Смалько, Є.М.Смірнова, Ю.В.Триус, Т.І.Чепрасова, А.М.Ясинський та інші.
Попри велике наукове i практичне значення проведених досліджень ряд аспектів потребує подальшого вивчення. Зокрема, недостатньо розроблені питання методики навчання дисциплін математичного циклу із застосуванням ІКТ у ВНЗ педагогічного профілю.
Все більш зростаючі вимоги до підготовки майбутнього вчителя математики, необхідність наблизити його підготовку до сучасних вимог щодо педагогічної діяльності потребує перегляду методичної системи навчання математики в університетах та педагогічних ВНЗ. З появою та впровадженням в практику навчання математики сучасних засобів ІКТ намітилися досить суттєві зрушення у розв'язанні даної проблеми.
Об'єктом дослідження є комп'ютерно–орієнтована методична система навчання методиці математики у вищих педагогічних навчальних закладах.
Предметом дослідження є процес вивчення студентів курсу “Застосування ІКТ в процесі навчання математики»
Мета дослідження — Розробити методичні рекомендації проведення лабораторних занять з курсу “Застосування ІКТ в процесі навчання математики»
Завдання дослідження :
проаналізувати стан досліджуваної проблеми, виявити можливості вдосконалення методичної системи навчання математики в педагогічному ВНЗ за рахунок широкого впровадження засобів ІКТ в навчальний процес;
дібрати необхідні математичні пакети для впровадження у навчальний процес, виконати розробки для комп'ютерної підтримки навчально–пізнавальної діяльності студентів при навчанні математики, розробити плани — конспекти лабораторних занять.
Методи дослідження :
теоретичний аналіз науково–методичної та психолого–педагогічної літератури з проблеми дослідження;
аналіз ППЗ та професійних математичних пакетів на предмет їх використання в навчальному процесі;
співбесіди з викладачами, які проводять лекційні та практичні заняття з математики.
РОЗДІЛ І ТЕОРЕТИЧНІ ЗАСАДИ З КУРСУ «ЗАСТОСУВАННЯ ІКТ У ПРОЦЕСІ НАВЧАННЯ МАТЕМАТИКИ»
Дата: 2019-05-28, просмотров: 383.