Огляд науково-методичної літератури, власні багаторічні дослідження Октайя Мирзоєва і Бориса Єрмолаєва, а також стаття М. Богена й О. Фетисова «Загадка тактики бігу на 100 м. [15. с.70], спонукали нас досліджувати проблему варіативності тактичної побудови спринтерського бігу.
Переосмислення результатів досліджень теорії і методики бігу на 100м, опублікованих ще наприкінці 40-х — початку 50-х років XX століття, а також власні дані дозволили М. Богену й О. Фетисову припустити, що тактичні розкладки в бігу на 100 м, як не дивно, існують, зокрема в бігунів високої кваліфікації. У підтвердження цього вони привели динаміку швидкості і часу пробігу 10- і 20-метрових відрізків дистанції Бенджаміном Джонсоном і Карлом Льюисом, зафіксовану під час бігу на 100 м на великих міжнародних змаганнях.
На підставі аналізу всього трьох результатів змагання автори роблять висновок про правомірність своїх теоретичних побудов по тактиці бігу на «стометрівці». Більш того, на їхню думку, практичний дозвіл цього питання виведе російських спринтерів із кризи.
Скажемо відразу, ми дотримуємо (і постараємося це обґрунтувати) іншої точки зору. В основі концепції М. Богена й О. Фетисова лежить формула, запропонована на початку 50-х років групою вчених ЛНИИФКа під керівництвом Б.Взорова. Оцінка результату в бігу на 100 м виводилася за часом пробігу відрізка 0—30 м (старту і стартового розгону, ТСТ=ТД+ +0,8 с), часу бігу на ЗО м з ходу (Тд) і часу пробігу останніх 10 м дистанції (Тф=Тд/3):
Трек-Тст+2Тд+Тф, відкіля випливає, що Трск=10/ЗТд+0,8с.
Далі, на думку М. Богена й О. Фетисова, тактичне (іншими словами, свідоме) регулювання швидкості бігу по дистанції дозволить вивести висококваліфікованого спринтера на заздалегідь запланований результат. Причому в практичній реалізації схеми висновку на заплановану швидкість бігу відзначається, що вихід на цю швидкість бігу на відрізку 60 м (чому не ЗО м, відповідно до запропонованої формули?) автоматично дозволить спортсмену стабільно демонструвати запланований результат у бігу на 100 м. Виходячи з уже згаданих співвідношень випливає, що результат бігу на 100 м редукується до часу пробігу ЗО м с/г з використанням поправочної константи 0,8 с.
Аналіз приведеного в тій же статті графіка динаміки швидкості бігу на 100 м (по 10-метрових відрізках) двох спортсменів демонструє досить складну конфігурацію кривої (багато в чому визначену швидкістю протікання біохімічних і нейрофизиологических процесів в організмі), якісно екстраполювати яку не представляється можливим ні по 30-метровому, ні навіть по 60-метровому відрізку дистанції.
Однак необхідний якісний, статистично представницький і достовірний аналіз структури розподілу швидкості пробігу окремих відрізків дистанції для рішення задачі моделювання тактичних особливостей бігу на 100 м.
Як відомо, біг на 100 м фахівці підрозділяють на старт і стартовий розгін (відрізок дистанції 0—30 м), біг по дистанції (відрізки 30—60 м 60—80 м) і фінішування (відрізок 80—100 м). Цей поділ обгрунтовується формальними задачами, розв'язуваними бігунами на біохімічному, біомеханічному, психологічному рівні.
Ми проаналізували результати змагань бігунів на 100 м, показані на Олімпійських іграх, чемпіонатах світу, міжнародних і всеросійських змаганнях. Відібрані дані досить рівномірно розподілилися на інтервалі від 9,79 до 10,90 (вибірка склала 208 результатів).
Найбільш адекватною математичною моделлю, що описує «тактичну розкладку сил» спортсмена, поява можливих акцентів у проходженні зазначених відрізків дистанції, є динаміка розподілу відносного часу пробігання відрізків у залежності від результату:
Т%і=100Ті/Т100
де: Т%і — відносний час пробігу 1-го відрізка дистанції (у відсотках); Ті — час на і-м відрізку дистанції; Т100 — спортивний результат у бігу на 100 м.
Так, результат 9,86, показаний рекордсменом світу на цій дистанції М.Гріном на чемпіонаті світу в Афінах у 1997 році, являє собою наступне: розподіл часу по відрізках: 3,80; 2,60; 1,71 і 1,75 з, що складає - 38,54; 26,37; 17,34 і 17,75% від спортивного результату бігу на 100 м. Дослідження припускає виявити статистичний взаємозв'язок відносного часу пробігу кожного відрізка з результатом.
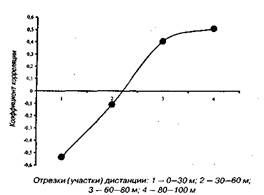
На мал. 1—4 представлені досліджувані результати, розташовані на кореляційному полі разом з апроксимуючої діаграму розсіювання, лінією регресії (по відрізках дистанції). На мал. 5 дана оцінка коефіцієнта парної кореляції на різних ділянках дистанції.
|
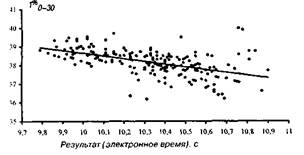
Рис 1 Розподіл відносного часу пробігання старту і стартового розбігу 0-30м
|
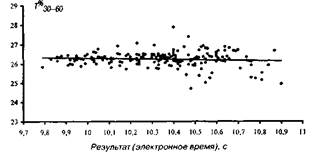
Рис 2 Розподіл відносного часу бігу по дистанції 30-60м
|
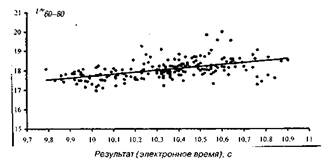

Рис 3 Розподіл відносного часу бігу по дистанції 60-80м
|
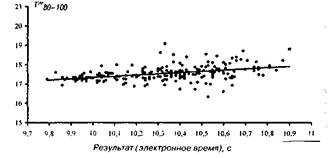

Рис 4 Розподіл відносного часу бігу на фінішному відрізку 80-100м
|
Рис 5 Коефіцієнт кореляції відносного часу пробігання різних відрізків дистанції 100 м і спортивного результату
Для практичного використання пропонованих модельних оцінок приведемо всі чотири прямі рівняння регресії, що ми одержали в наших дослідженнях.
Т%0-30=-1,486Т100+53,509
Т%30-60=-0,165Т100+27,951
Т%60-80=0,632100+11,010
Т%80-100=1,004Т100+7,676
Де Т100 — спортивний результат у бігу на 100 м,
(Т%0-30 Т%30-60 Т%60-80 Т%80-100 Т%80-100) — розподіл відносного часу пробігу по відрізках дистанції, причому коректність моделі забезпечується виконанням співвідношення
Т%0-30 +Т%30-60 +Т%60-80 +Т%80-100=100%
Адекватність статистичної моделі, потужність прогнозованих можливостей рівнянь регресії забезпечуються надзвичайно низькими погрішностями рівнянь, що складають, як показали розрахунки, що випливають величини: 1,5; 1,4; 2,0; 2,3% відповідно. Розташування вибірок на кореляційному полі (мал. 1—4), а також точність модельних оцінок (точність прогнозування) дозволяють установити існування загальної, універсальної і збалансованої тимчасової структури бігу на 100 м і деякі закономірності деформації цієї структури в залежності від спортивного результату.
Основна закономірність полягає в тому, що при поліпшенні спортивного результату спринтера інтенсивність росту швидкості пробігу окремих відрізків дистанції плавно зростає в міру видалення спортсмена від старту. При цьому негативна кореляція цього показника для ділянки 0—З0 м говорить не про погіршення часу пробігу цього відрізка для досягнення більш високого результату, а про відносно слабкий ріст цього показника. Іншими словами, фізіологічні і, отже, педагогічні резерви швидкості в бігу на 100 м варто шукати спринтеру і тренеру в бігу по дистанції (30—60 і 60—80 м) і особливо на фінішному відрізку (80—100 м). З ростом результату певні обмеження фізіологічних резервів спортсмена зв'язані з тенденцією вирівнювання швидкості бігу на останньому (80—100 м) і передостанньому (60—80 м) ділянці дистанції (див. таблицю).
Підкреслюючи фізіологічний характер цих резервів, ми хочемо акцентувати увагу на закономірностях, представлених на мал. 1 — 5 і демонстрируючих перспективні тенденції росту результатів. Ці закономірності носять (в рамках банальних статистичних погрішностей) загальний характер, визначаються і лімітуються, у першу чергу, деякими фізіологічними (у тому числі біохімічними і нейродина-мічними) обмеженнями і не дозволяють інтерпретувати дані на користь існування тактичних акцентів бігу по дистанції. Варто обмовитися, що досліджувані нами результати отримані в критичних, з погляду результату, змаганнях (тобто спортивний результат для спортсменів важливий). Крім того, мал.1—4 показують, що дисперсія досліджуваних вибірок, а відповідно і погрішності виявлених закономірностей, мінімальні для результатів у діапазоні від 9,80 до 10,20.
Передбачувані тактичні акценти в бігу, виявлені в статті М. Богена й О. Фетисова, засновані на статистично недостовірних даних — аналізі трьох (а фактично двох) результатів змагання. Крім того, тактичні акценти повинні значимо відрізнятися від загальних фундаментальних закономірностей зміни структури швидкості бігу по відрізках дистанції. У противному випадку, природні біохімічні процеси зміни енергетичного забезпечення бігу можливо інтерпритувати як свідомі «включення» і «виключения» спортсмена.
При педагогічній інтерпритації даних необхідно враховувати наступне: зазначені «включення» і «вимикання».
Швидкості повинні бути досить достовірні, як з погляду отримання вихідних даних, так і їхній математичній обробці (моделі), не кажучи вже про обґрунтованість і коректність застосовуваних технологій дослідження (якщо, наприклад, фотодіодні пристрої, що реєструють час бігу, стояли б не через кожні 10 м, а через кожний метр дистанції, то, можливо, кількість виявлених локальных екстрімумів істотно б зросло). Але ще Арістотель попереджував, що при вивченні будь-якого предмета не слід прагнути до більшої точності, ніж допускає природа предмета.
Крім того, у випадку свідомого керування швидкістю по дистанції це говорило б про те, що спортсмен у стані свідомо інтерпритувати, контролювати і керувати (кінематично коректувати) усіма процесами, що відбуваються в організмі, у надзвичайно коротких тимчасових інтервалах і при граничних м'язових зусиллях. Безумовно, м'язові відчуття спортсмена надають йому можливість, контролювати швидкість бігу, однак тимчасові показники і потужності характеристики цього контролю не можуть дозволити з необхідною точністю здійснити подібні тактичні побудови.
Результати цього контролю не можуть дозволити з необхідною точністю здійснити подібні тактичні побудови.
Але головне протиріччя проблеми розробки тактичних вариантів побудови бігу на 100 м полягає в наявності єдиної універсальної структури бігу, визначеної відповідними психофізіологічними механізмами і здатністю чи нездатністю індивідуальних м'язових відчуттів спортсмена перебудуватися під цю структуру. Розвиток почуття швидкості» (здатності почувати і регулювати швидкість бігу) і розпізнавальної чутливості рухів, особливо при максимальних проявах функцій організму, є перспективним засобом тренування, спрямованим на відчуття загальної схеми бігу, її перспективних тенденцій.
Результати моделювання єдиної універсальної тимчасової структури бігу на 100 м | ||||
| Результат (с) | Час бігу на окремих ділянках дистанції (с) (складова спортивного результату, %) | |||
| 0-30 м | 30-60 м | 60-80 м | 80-100 м | |
| 9,50 9,60 9,70 9,80 9,90 10,00 10,10 10,20 10,30 10,40 10,50 10,60 10,70 10,80 10,90 11,00 | 3,74 (39,39) 3,77 (39,24) 3,79 (39,09) 3,82 (38,95) 3,84 (38,80) 3,87 (38,65) 3,89 (38,50) 3,91 (38,35) 3,94 (38,20) 3,96 (38,05) 3,98 (37,91) 4,00 (37,76) 4,02 (37,61) 4,05 (37,46) 4,07 (37,31) 4,09 (37,16) | 2,51(26,38) 2,53 (26,37) 2,56 (26,35) 2,58 (26,33) 2,61 (26,32) 2,63 (26,30) 2,65 (26,28) 2,68 (26,27) 2,70 (26,25) 2,73 (26,24) 2,75 (26,22) 2,78 (26,20) 2,80 (26,19) 2,83 (26,17) 2,85 (26,15) 2,88 (26,14) | 1,62 (17,01) 1,64 (17,08) 1,66 (17,14) 1,69 (17,20) 1,71 (17,27) 1,73 (17,33) 1,76 (17,39) 1,78 (17,46) 1,80 (17,52) 1,83 (17,58) 1,85 (17,65) 1,88 (17,71) 1,90 (17,77) 1,93 (17,84) 1,95 (17,90) 1,98 (17,96) | 1,64 (17,21) 1,66 (17,31) 1,69 (17,41) 1,72 (17,52) 1,74 (17,62) 1,77 917,72) 1,80 (17,82) 1,83 (17,92) 1,86 (18,02) 1,88 (18,12) 1,91 (18,22) 1,94 (18,32) 1,97 (18,42) 2,00 (18,52) 2,03 (18,62) 2,06 918,72) |
Інша група факторів, облік впливу яких не знайшов своє відображення в аналізованій статті, зв'язана з впливом психологічної підготовки спринтера на його психофізіологічну готовність. Наприклад, у реальних умовах змагання може скластися ситуація, коли спортсмен твердо упевнений, що на визначеній ділянці дистанції він ясно відзначав (і активно генерував) суб'єктивне «включення» потужності бігу, а кінематична картина бігу неупереджено зафіксувала «скидання» швидкості і навпаки. Це зв'язано з індивідуальними особливостями моторного контролю в спортсмена, з одного боку, і психофізіологічними обмеженнями його якостей, з іншої.
Результати наших досліджень пропонують скорегувати розміщення акцентів у структурі пробігу окремих відрізків 100-метрової дистанції, що нагадує рукопис партитури Франца Листа, де на першій сторінці зазначено грати «швидше», на другій — «дуже швидко», на третій — «набагато швидше», на четвертій — «швидко, як тільки можливо» і все-таки на п'ятій — « ще швидше»!
Результати моделювання можуть служити специфічним критерієм оптимальності тимчасової структури конкретного результату в бігу на 100 м при визначенні наявних фізіологічних резервів на окремих відрізках і, відповідно, координаторами зсуву акцентів у плануванні тренувального навантаження. Так, приміром, результат, показаний М. Гріном (9,86), являє собою наступне: розподіл часу по ділянках дистанції — 3,80; 2,60; 1,71 і 1,75, а на основі рівнянь регресії припускає — 3,831; 2,596; 1,700 і 1,733. Модельовані оцінки дозволяють припустити, що унікальна збалансованість пробігу всіх ділянок дистанції (відхилення показаного результату від прогнозованого оптимального на кожній ділянці дистанції складає менш 1%), феноменальне почуття швидкості в цілісній структурі бігу дозволили М.Грінові досягти настільки високого результату. Можливо, ці особливості стали базою для встановлення ним світового рекорду (9,79).
Відзначимо, що модельне пророкування результату 9,75 припускає наступне: розподіл часу по ділянках дистанції — 3,805; 2,568; 1,674 і 1,703. Ми вважаємо, що при найвищому рівні швидкісних можливостей і швидкісної витривалості, у рамках фізіологічних обмежень спринтерів (мал. 1—4), для досягнення результату 9,75 сучасним атлетам необхідно значно поліпшити час на другій половині дистанції (особливо на останній третині), при загальній збалансованості тимчасової структури бігу, що, наприклад, продемонстрував М. Грін для результату 9,86.
Труднощі збільшення швидкості бігу на останніх ділянках дистанції (60—80 і 80—100 м), а фактично наближення спринтером до своєї фізіологічної границі ми продемонструємо наступними оцінками. Визначимо кращі результати пробігу окремих відрізків дистанції (рекорди пробігу цих відрізків) по всій сукупності наданих у дослідженні результатів. Вони складають наступний розподіл часів — 3,72; 2,53; 1,67 і 1,70, що надає уяву про можливості сучасних спринтерів на окремих відрізках дистанції. Регресивна модель на основі кожного з цих показників дозволяє розрахувати можливий спортивний результат, при збалансованості проходження всієї дистанції. Одержимо наступний розподіл — 9,41; 9,59; 9,73 і 9,74. Приведені оцінки ще раз підтверджують положення, відповідно до якого основними факторами бігу, що лімітують, на 100м є можливості і резерви спринтера на відрізку 60—100 м.
Динаміка пробігання окремих відрізків, відбита в єдиній структурі, припускає цілісний характер і загальний фундаментальний механізм генезису цієї структури. Єдино, з чим ми можемо погодитися, маючи у виді статті М. Богена й О. Фетисова, так це з тим, що відносний час пробігу відрізка 30—60 м дистанції мінімально корелює зі спортивним результатом бігу на 100 м (див. мал. 2 і 5). Це говорить про те, що зазначена величина є в деякому змісті руховим інваріантом цілісної структури бігу. Відносний час пробігу цього відрізка дистанції є практично незмінною величиною для великого діапазону показуваних результатів. Іншими словами, час пробігу ділянки 30—60 м змінюється одночасно і пропорційно з результатом на 100 м і, відповідно, зазначена величина є своєрідним індикатором інтенсивності росту спортивного результату.
Біг на 100 м являє собою єдину вправу, внутрішню зв'язаність якого визначають психофізіологічні процеси в рамках індивідуальних для кожного спортсмена особливостей біомеханічної структури бігу (техніки).
Єдність тимчасової структури вправи ми розуміємо в такий спосіб: внутрішня логіка вправи дозволяє по будь-якому фрагменті (на підставі зазначених закономірностей) відновити найбільш раціональну цілісну картину. Практично так і відбувається знаючи, наприклад, лише час перших 30м. у бігу на 100м., ми можемо реконструювати найбільш ефективну «тимчасову розкладку сил спортсмена-» по всій дистанції (і єдино можливим способом!), виходячи з результатів статистичного моделювання. Обмовимося, що в реальності ми знаємо не відносний результат пробігу перших 30 м дистанції Т%0-30-, а абсолютний результат цього відрізка Т0-30, де Т%0-30=100 Т0-30/Т100. Підставляючи це вираження в перше рівняння регресії, одержуємо квадратне рівняння відносно Т100 . При його вирішенні знаходимо два корені, однак тільки один з них пасує умовам нашої задачі. Отримане значення Т 100 підставляємо в рівняння регресії, що залишилися, і одержуємо єдину збалансовану «тимчасову розкладку сил спортсмена» у бігу на всій 100-метровій дистанції. Аналогічно оптимальний розклад сил відновлюється за часом пробігу будь-якого відрізка дистанції. Уміння найбільш ефективним методом перебудуватися (скорегувати свої м'язові почуття) під виявлену загальну структуру бігу і являє собою «універсальну тактику» для бігу на конкретний результат. Пропонована модель на великому діапазоні результатів узагальнює нею сукупність особливостей фізіологічного забезпечення бігу на 100 м висококваліфікованими спринтерами з більш ніж задовільною точністю.
На закінчення хотілося б відзначити, що наші дослідження в пропонованому напрямку не можна розглядати як остаточне й однозначне рішення проблеми.
По-перше, ми не стверджуємо, що пропонована модель не може бути удосконалена, у тому числі самим радикальним способом.
По-друге, необхідно провести порівняльне дослідження виявленої структури бігу на 100 м і діапазону можливих змін подібних співвідношень і бігу на 200 і 400 м. Очевидний специфічний науково-методичний інтерес подібні дослідження здобувають у бар'єрних дистанціях.
По-третє, концепція бігу на 100 м не вичерпується дослідженням моделей, заснованих тільки на кінематичних показниках — ; можливий пошук інших кореляторів бігу (психологічних, біохімічних, фізіологічних і ін.).
Дата: 2019-05-28, просмотров: 377.