1 участок -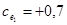 
; 
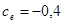
2 участок -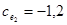 
На каждом участке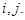 
находим средний коэффициент:
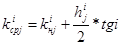
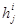- протяженность участка с однозначной эпюрой на определенном участке.
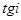- тангенс угла наклона эпюры ветрового давления на участке с однозначной эпюрой (рис. 3).
;
;
;
;
;
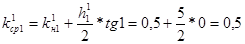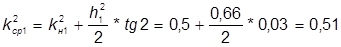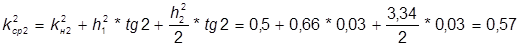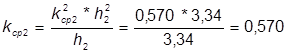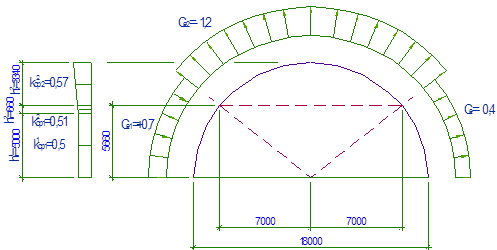
Рис. 3 - Схема аэродинамических коэффициентов и коэффициентов k
Расчетное значение ветровой нагрузки
;
;
;
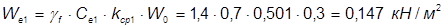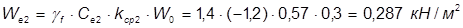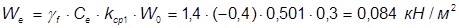Статический расчет
Наиболее нагруженными являются два промежуточных ребра, так как нагрузка, воспринимаемая ребром, собирается с двух полупролетов справа и слева от ребра (рис. 4).
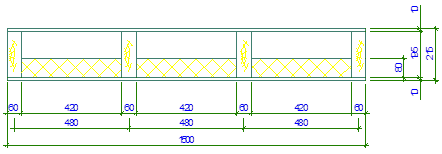
Рис. 4 - Поперечное сечение плиты
Ширина площадки опирания на верхний пояс несущей конструкции 8 см, расчетный пролет плиты: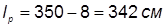 
.
Плита рассчитывается как балка на 2-х опорах.
Равномерно распределенная нагрузка на расчетное среднее ребро равна
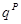= 6,435·0,48 = 3,09 кН/м2;
Расчетный изгибаемый момент: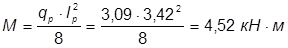 
;
Поперечная сила: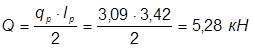 
;
Определение геометрических характеристик расчетного сечения плиты
Расчет конструкции плиты выполняем по методу приведенного поперечного сечения в соответствии с п.4 СНиП 2.03.09-85 Асбоцементные конструкции [1].
В соответствии с п. 4.3 [1] для сжатых обшивок принимаем часть обшивки, редуцируемой к ребру:
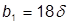= 18 см, с двух сторон – 36 см;
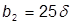= 25 см, с двух сторон – 50 см, т.е. сечение получается несимметричным (рис. 5).
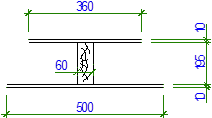
Рис. 5 - Расчетное сечение плиты
Отношение модуля упругости обшивки к модулю упругости каркаса равно:
na=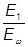 
= 
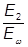=(1,4·104)/(1·104) = 1,4.
Определяем положение нейтральной оси сечения по формуле без учета податливости соединений ребер каркаса с обшивками
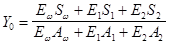
Отношение модуля упругости обшивки к модулю упругости каркаса равно:
= 
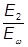=(1,4·104)/(1·104) = 1,4.
Y о=(19,5·6·(19,5/2+1)+1,4·36·1·(19,5+1+1/2)+1,4·50·1·0,5)/[19,5·6+(36+50)·1,4]=9,90 см.
Определяем моменты инерции каркаса и обшивок.
Собственный момент инерции каркаса
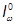= 6·19,53/12 = 3707 см4.
Момент инерции каркаса относительно найденной нейтральной оси
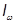= 3707 + 19,5·6· (19,5/2+1 – 9,9)2 = 3792 см4.
Моменты инерции обшивок относительно нейтральной оси:
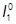= [36·13/12 + 36(1+19,5+0,5 – 9,9)2]1,4 = 6214 см4;
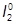= [50·13/12 + 50(9,9 –0,5)2]1,4 = 6191 см4.
Суммарный момент инерции сечения:
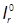= 3792 + 6214 + 6191 = 16197 см4.
Шурупы в плите расставлены с шагом 200 мм, т.е.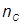 
=9 – число срезов шурупов на половине пролета (3500/(2·200)=8,75).
Статические моменты относительно нейтральной оси будут равны:
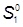= 36(1+19,5+0,5 – 9,9)1,4 = 559,4 см3;
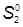= 50(9,9 – 0,5)1,4 = 658 см3.
Определяем коэффициент податливости соединений т (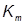 
= 1 шурупы из стали, 
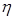= 62·10-5 при диаметре шурупов 0,4 см):
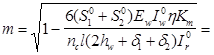
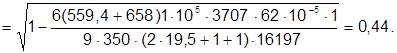
Определяем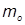 
:
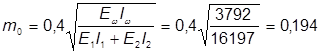
т > 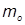, т.е. для расчета прочности каркаса принимаем т = 
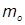=0,194;
для расчета прочности обшивок принимаем т = 0,44.
Положение нейтральной оси определяем с учетом коэффициента податливости соединений ребер каркаса с обшивками при т = 0,44, т.е. при т для определения напряжений в обшивках.
Определяем положение нейтральной оси:
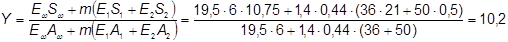см.
Моменты инерции будут равны:
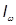= 3707 + 19,5·6·(19,5/2+1 – 10,2)2 = 3742 см4;
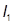= [36·13/12 + 36·(1+19,5+0,5 – 10,2)2]·l,4 = 5883 см4;
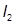= [50·13/12 + 50·(10,2 – 0,5)2]·1,4 = 6592 см4.
Для определения напряжений в ребре каркаса положение нейтральной оси определяем при 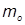= 0,194:
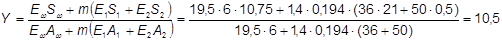см.
Моменты инерции:
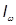= 3707 + 19,5·6·(19,5/2+1 – 10,5)2 = 3711 см4;
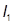= [36·13/12 + 36(1+19,5+0,5 – 10,5)2]l,4 = 5561 см4;
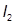= [50·13/12 + 50(10,5 – 0,5)2]1,4 = 7723 см4.
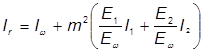
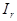= 3711 + 0,442(5561 + 7723) = 6283 см4.
Дата: 2019-05-28, просмотров: 186.
