Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Существуют следующие формы комплексных чисел: алгебраическая (x+iy), тригонометрическая (r(cos 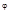+isin 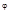)), показательная (reⁱ ).

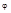Всякое комплексное число z=x+iy можно изобразить на плоскости ХОУ в виде точки А(х,у).

Плоскость, на которой изображаются комплексные числа, называется плоскостью комплексного переменного z (на плоскости ставим символ z).

Ось ОХ – действительная ось, т.е. на ней лежат действительные числа. ОУ – мнимая ось с мнимыми числами.

x + iy - алгебраическая форма записи комплексного числа.

Выведем тригонометрическую форму записи комплексного числа.

 

;

 

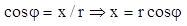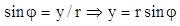
Подставляем полученные значения в начальную форму:

 

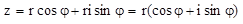, т.е.

r ( cos 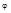+ isin 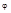) - тригонометрическая форма записи комплексного числа.

 

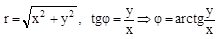
Показательная форма записи комплексного числа следует из формулы Эйлера:

 

, тогда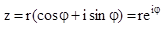

 

z=reⁱ 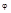 - показательная форма записи комплексного числа.

 

Действия над комплексными числами

1. сложение. z₁+z₂=(x1+iy1)+ (x2+iy2)=(x1+x2)+i(y1+y2);

2. вычитание. z₁-z₂=(x1+iy1)- (x2+iy2)=(x1-x2)+i(y1-y2);

3. умножение. z₁z₂=(x1+iy1)*(x2+iy2)=x1x2+i(x1y2+x2y1+iy1y2)=(x1x2-y1y2 )+i(x1y2+x2y1);

4. деление. z₁/z₂=(x1+iy1)/(x2+iy2)=[(x1+iy1)*(x2-iy2)]/[ (x2+iy2)*(x2-iy2)]=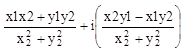

Два комплексных числа, которые отличаются только знаком мнимой единицы, т.е. z=x+iy (z=x-iy), называются сопряженными.

Произведение

- Если комплексные числа заданы в тригонометрической форме.

z1=r(cos 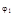+isin 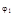); z2=r(cos 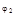+isin ).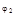

То произведение z1*z2 комплексных чисел находится: 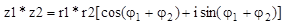, т.е. модуль произведения равен произведению модулей, а аргумент произведения равен сумме аргументов сомножителей.

- Если комплексные числа заданы в показательной форме.

; ;

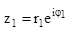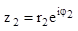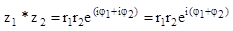
Частное

- Если комплексные числа заданы в тригонометрической форме.

 

 

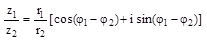
- Если комплексные числа заданы в показательной форме.

 

 

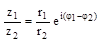
Возведение в степень

1. Комплексное число задано в алгебраической форме.

z=x+iy, то zⁿ находим по формуле бинома Ньютона:

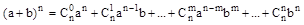
zⁿ=(x+iy)ⁿ.

 

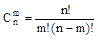- число сочетаний из n элементов по m (число способов, сколькими можно взять n элементов из m).

 

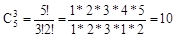; n!=1*2*…*n; 0!=1; .

 

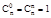Применяем для комплексного числа.

 

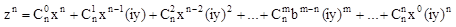
В полученном выражении нужно заменить степени i их значениями:

i⁰=1 Отсюда, в общем случае получаем: i^4k=1

i¹=i                          i^4k+1=i

i²=-1                       i^4k+2=-1

i³=-i                        i^4k+3=-i

i⁴=1

i⁵=i

i⁶=-1

Пример.

i³¹= i²⁸ i³=-i

i¹⁰⁶³= i¹⁰⁶² i=i

2. Если комплексное число задано в тригонометрической форме.

 

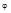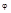z=r(cos +isin ), то

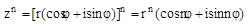- формула Муавра.

Здесь n может быть как “+” так и “-” (целым).

3. Если комплексное число задано в показательной форме:

 

 

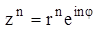
Извлечение корня

Рассмотрим уравнение: .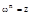

Его решением будет корень n–ой степени из комплексного числа z: .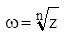

Корень n–ой степени из комплексного числа z имеет ровно n решений (значений). Корень из действующего числа n-ой степени имеет только одно решение. В комплексных – n решений.

Если комплексное число задано в тригонометрической форме:

z=r(cos 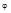+isin 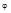), то корень n-ой степени от z находится по формуле:

 

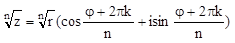, где к=0,1…n-1.

 

РЯДЫ

Числовые ряды

 

Пусть переменная а принимает последовательно значения а₁,а₂,а₃,…,а_n. Такое перенумерованное множество чисел называется последовательностью. Она бесконечна.

Числовым рядом называется выражение а₁+а₂+а₃+…+а_n+…= 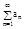 . Числа а₁,а₂,а₃,…,а_n – члены ряда.

Например.

а₁ – первый член ряда.

а_n – n-ый или общий член ряда.

Ряд считается заданным, если известен n-ый (общий член ряда).

 

 

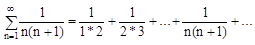
Числовой ряд имеет бесконечное число членов.

 

 

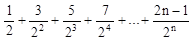
Числители – арифметическая прогрессия (1,3,5,7…).

n-ый член находится по формуле

 

а_n=а₁+d(n-1); d=а_n-а_n-1.

 

Знаменатель – геометрическая прогрессия.

 

b_n=b₁q^n-1; .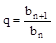

 

Рассмотрим сумму первых n членов ряда и обозначим ее Sn.

 

Sn=а1+а2+…+а_n.

 

Sn – n-ая частичная сумма ряда.

Рассмотрим предел: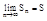

S - сумма ряда.

Ряда сходящийся, если этот предел конечен (конечный предел S существует).

Ряд расходящийся, если этот предел бесконечен.

В дальнейшем наша задача заключается в следующем: установить какой ряд.

Одним из простейших, но часто встречающихся рядов является геометрическая прогрессия.

 

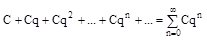, C=const.

Геометрическая прогрессия является сходящимся рядом, если 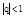, и расходящимся, если .

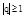Также встречается гармонический ряд (ряд 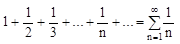). Этот ряд расходящийся.

Свойства числовых рядов

1. Если сходится а₁+а₂+а₃+…+а_n+…= 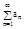, то сходится и ряд а_m+1+а_m+2+а_m+3+…, полученный из данного ряда отбрасыванием первых m членов. Этот полученный ряд называется m-ым остатком ряда. И, наоборот: из сходимости m-го остатка ряда вытекает сходимость данного ряда. Т.е. сходимость и расходимость ряда не нарушается, если прибавить или отбросить конечное число его членов.

2. Если ряд а₁+а₂+а₃+… сходится и его сумма равна S, то ряд Са₁+Са₂+…, где С= так же сходится и его сумма равна СS.

3. Если ряды а₁+а₂+… и b₁+b₂+… сходятся и их суммы равны соответственно S1 и S2, то ряды (а₁+b₁)+(а₂+b₂)+(а₃+b₃)+… и (а₁-b₁)+(а₂-b₂)+(а₃-b₃)+… также сходятся. Их суммы соответственно равны S1+S2 и S1-S2.

4. а). Если ряд сходится, то его n-ый член стремится к 0 при неограниченном возрастании n (обратное утверждение неверно).

 

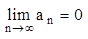- необходимый признак (условие) сходимости ряда.

б). Если 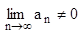 то ряд расходящийся – достаточное условие расходимости ряда.

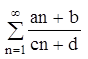-ряды такого вида исследуются только по 4 свойству. Это расходящиеся ряды.

Знакоположительные ряды