F(x,y”)=0

y’’=f(x)- решение этого уравнения находится путем двукратного интегрирования.

; ; ;

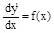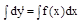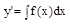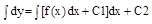
2. Когда дифференциальное уравнение явно не содержит у, т.е. F ( x , y ’, y ”)=0

С помощью замены у’=р; 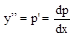 это уравнение приводим к уравнению первого порядка .

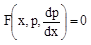3. Когда дифференциальное уравнение явно не содержит х, т.е. F ( y , y ’, y ”)=0.

С помощью замены y’=p, 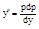 это уравнение приводим к уравнению первого порядка .

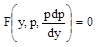Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Линейными однородными дифурами второго порядка с постоянными коэффициентами называются уравнения вида:

y’’+py’+qy=0,

где p и q – некоторые числа.

Составим характеристическое уравнение:

,

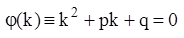которое получается из данного уравнения путем замены в нем производных искомой функции соответствующими степенями “к”. Причем сама функция заменяется единицей.

Если к1 и к2 – корни характериситического уравнения, то общее решение однородного уравнения имеет один из следующих трех видов:

1). 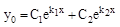, если к1 и к2 – действительные и различные, т.е.  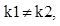D>0.

2). 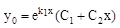, если к1 и к2 – действительные и равные, т.е. к1=к2, D=0.

3). 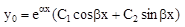, если к1 и к2 – комплексные, т.е. 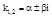; D<0.

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Имеют вид:

,

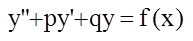где p и q– некоторые числа.

Общее решение имеет вид: 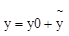, где

y0 - общее решение соответствующего однородного уравнения; 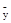- частное решение соответствующего однородного уравнения.

Т.е. для нахождения общего решения неоднородного уравнения ‘у’, сначала находят общее решение соответствующего однородного уравнения у0, а затем частное решение 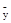, и складывают их.

Частное решение неоднородного уравнения находится методом неопределенных коэффициентов.

Для нахождения частных решений 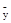 рассмотрим несколько случаев.

1. Пусть правая часть f(x) имеет вид:

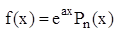, где P_n(x) – многочлен n–ой степени.

Тогда возможны следующие 3 случая:

А). Если ‘а’ не является корнем характеристического уравнения k²+pk+q=0, то частное решение 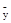 имеет вид: 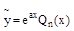, где Q_n(x) – многочлен той же степени, что и P_n(x), только с неопределенными коэффициентами.

Например.

P_n(x)=8 - многочлен 0-ой степени (n=0). Q_n(x)=A;

P_n(x)=2x-3 - многочлен 1-ой степени (n=1). Q_n(x)=Ax+B;

P_n(x)=x² - многочлен 2-ой степени (n=2). Q_n(x)=Ax²+Bx+C;

P_n(x)=3x³-3x - многочлен 3-ей степени (n=3). Q_n(x)=Ax³+Bx²+Cx+D.

Замечание. Многочлен Q_n(x) всегда должен быть полный, т.е. содержать все степени х. Коэффициенты А,В,С,Д и т.д. находим по методу неопределенных коэффициентов непосредственно при решении каждого конкретного уравнения.

Б). Если а является однократным корнем характеристического уравнения k²+pk+q=0, то есть совпадает с одним из корней характеристического уравнения, то частное решение 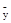 имеет вид: .

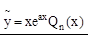В). Если а является двукратным корнем характеристического уравнения k²+pk+q=0, то есть совпадает с двумя корнями характеристического уравнения, то частное решение 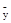 имеет вид: .

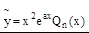Итог.

Если 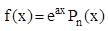, то 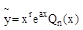, где r– кратность корня ‘а’ в характеристическом уравнении, т.е. r=0, если ‘а’ не есть корень; r=1, если ‘а’ совпадает с одним из корней; r=2, если ‘а’ совпадает с двумя корнями.

2. Если правая часть f(x) имеет вид:, 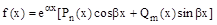где P_n ( x )–многочлен n–ой степени; Q_m ( x )-многочлен m–ой степени.

Тогда возможны следующие два случая:

А). Если 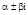 не является корнем характеристического уравнения k²+pk+q=0 ( 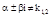), то частное решение  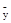имеет вид: 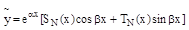, где S_N(x), T_N(x)–многочлены степени N с неопределенными коэффициентами, где N=max из n и m (N=max{n,m}), т.е. степень N многочленов S_N(x) и T_N(x) равна наибольшей из степеней многочленов P_n(x) и Q_m(x).

Б). Если 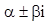 является корнем характеристического уравнения k²+pk+q=0 ( 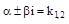), то частное решение  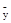имеет вид: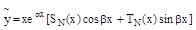

Замечание.

- Если в правой части f(x) неоднородного уравнения во 2 случае отсутствует одно из слагаемых, т.е. P_n(x)=0 или Q_m(x)=0, то частное решение 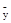 все равно записывается в полоном виде.

- Если правая часть f(x) неоднородного уравнения в 1 и 2 случаях есть сумма нескольких функций (f(x)= f₁(x)+ f₂(x)+… f_n(x)), то .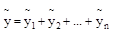

- Так же рассматриваем все комбинации при расчете 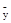: cosx, sinx, xcosx, xsinx,x²cosx, x²sinx.

КОМПЛЕКСНЫЕ ЧИСЛА

Комплексным числом (z) называется выражение z=x+iy, где х и у- действительные числа, i-мнимая единица.

i определяется: i²=-1 , отсюда .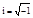

х- действительная часть (x=Rez);

у- мнимая часть (y=Imz).