Теоретической и методологической основой дипломной работы послужили труды отечественных и зарубежных ученых, посвященные проблемам инвестиционно-строительного комплекса. В работе использовались монографии, брошюры, статьи в сборниках и периодических изданиях по вопросам, рассмотренным в дипломной работе. В качестве фактических материалов использовались данные Государственного Комитета Статистики [31] и статистический сборник по Ивановской области [31], а также специальные исследования.

В дипломной работе использованы различные методы и приемы статистики [28]. К ним относятся средние и относительные величины, группировки, показатели динамики и другие. Наибольшее значение в анализе имеет метод группировок, который, в сочетании с другими приемами и методами, позволяет учитывать специфику сводного анализа и на этой основе выявлять особенности использования экономических законов в процессах освоения инвестиционных вложений и характеристики строительного производства. В анализе производственной деятельности строительных предприятий большое значение имеет и группировка по формам собственности, объему выполненных работ, численности занятых, числу предприятий. Широко применяются в анализе средние и относительные величины. Они могут использоваться самостоятельно или в сочетании с другими методами, например, группировкой. Особый интерес представляет анализ структуры и ее изменения.

Для изучения влияния на экономику строительства различных структурных изменений следует использовать показатели структурных сдвигов (изменение структуры во времени) и структурных различий (сравнение структур различных объектов). Основными из них являются:

Абсолютный прирост долей (удельных весов):

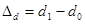 или ,

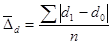где n – число интервалов времени,

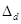 - абсолютный прирост удельного веса,

d1 и d0 – удельный вес структурной части в отчетном и базисном периодах.

Обобщающие показатели структурных сдвигов и структурных различий, например, линейный коэффициент структурных изменений:

,

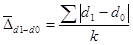где 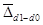 - средний прирост по совокупности в целом,

k – Число структурных составляющих.

Роль статистики состоит также в изучении взаимосвязей между различными показателями рассматриваемой деятельности, в данном случае, строительства. Это изучение важно не только для установления самого факта наличия связей, но и для научно-обоснованного прогнозирования. Поэтому важно придать выявляемым связям математическую определенность, ведь без их количественных оценок невозможно довести результаты экономических разработок до практического применения.

Статистические показатели могут состоять между собой в различных типах связи:

балансовая характеризует взаимосвязь между источником формирования ресурсов и их потреблением

компонентная, когда изменение статистического показателя определяется изменениями его компонентов (сомножителей); это используется в индексном методе, например:

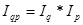, где

Iqp – индекс объема строительно-монтажных работ в фактических ценах;

Iq – то же в сопоставимых ценах;

Ip – индекс сметных цен.

Факторная проявляется в согласованной вариации изучаемых показателей, один из которых считается факторным, другой – результативным.

Корреляционная, при которой изменение результативного признака обусловлено изменением факторного лишь частично, так как возможно влияние прочих факторов. По своему характеру корреляционные связи являются соотносительными.

В отличие от функциональной связи, проявляющейся с одинаковой силой у каждой единицы изучаемой совокупности, в корреляционном при одном значении учтенного фактора возможны различные значения результативного признака. Поэтому для изучаемой совокупности в целом здесь устанавливают соотношение, в котором изменению фактора соответствует среднее изменение результата. Таким образом, корреляционные связи проявляются в совокупности в целом.

При изучении корреляционной связи показателей строительной деятельности перед статистикой ставят следующие задачи:

проверка положений экономической теории о возможности связи между изучаемыми показателями и придание выявленной связи аналитической формы;

установление количественных оценок тесноты связи, характеризующих силу влияния факторных признаков на результат.

Для выявления закономерности развития инвестиционно-строительных процессов во времени и их прогнозирования используют методы выравнивания динамических рядов.

укрупнение интервалов применяется для выявления тренда в рядах данных, колебания в которых затушевывают основную тенденцию развития. Он состоит в простом объединении мелких периодов в более крупные интервалы и суммировании данных внутри новообразованных периодов;

при использовании метода скользящей средней каждую новую среднюю величину рассчитывают, отбрасывая один уровень слева и добавляя один уровень справа. Например: 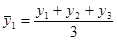,  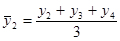и т.д.

Для выравнивания динамических рядов можно использовать различные математические функции:

уравнение прямой линии: ;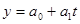

степенную функцию: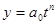

уравнение гиперболы: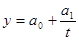

уравнение параболы: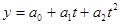

показательную функцию: ,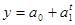

где y – уровень изучаемого показателя в зависимости от времени, t – период времени, a0, a1,a2 – параметры модели.

Параметры модели определяются путем решения системы уравнений, полученных методом наименьших квадратов по формулам, приводимым в учебниках статистики.

На основе выявленных тенденций развития основных показателей строительства можно спрогнозировать их на ближайшее будущее, то есть провести экстраполяцию:

по средним абсолютным приростам показателя в ретроспективе и их распространением на перспективу:

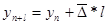
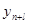 - экстраполируемый уровень,

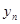 - конечный уровень динамического ряда,

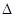 - средний абсолютный прирост показателя в базисной динамике,

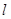 - период упреждения.

При экстраполяции уровня показателей со стабильными темпами роста применяется формула:

,

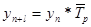где 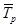 - средний темп роста в базисной динамике

С использованием трендов развития показателей, полученных при выравнивании динамических рядов, например: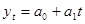

Результаты экстраполяции обычно даются в виде вероятностных интервальных оценок. Для определения доверительного интервала используется следующая формула:

,

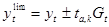где 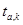 - коэффициент Стьюдента,

Gt – средняя квадратическая ошибка тренда:

,

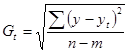n – Число уровней базисного ряда динамики

m – Число параметров модели (для уравнения прямой m=2).

Вероятностные границы интервала прогнозируемого явления:

.

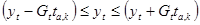Нужно иметь в виду, что экстраполяция в рядах динамики носит не только приближенный, но и условный характер, поэтому ее следует рассматривать лишь как предварительный этап разработки прогнозов.