Характерной чертой математической информации является использование сложной и высокоразвитой двумерной символьной системы обозначений. Однако, как писал J. R. Pierce в своей книге по теории коммуникации, математика и ее нотация не должны рассматриваться как одно и то же. Математические идеи существуют независимо от способа их представления. Тем не менее, взаимосвязь между значением и обозначением весьма тонка, и в возможности представлять и манипулировать идеями в символьной форме кроется значительная мощь математического аппарата, как инструмента описания и анализа. Основная трудность при внедрении математики в World Wide Web состоит в том, чтобы зафиксировать как представление, так и содержание (то есть значение) таким образом, чтобы в документах максимально использовать высокоразвитую систему математической нотации и потенциал взаимодействия в электронных средствах информации.
Математическая система обозначений постоянно развивается, так как люди постоянно совершенствуют способы представления идей. Даже стандартная система обозначения арифметических действий прошла через удивительное многообразие стилей, включая множество ныне несуществующих, поддерживающих математические обозначения своего времени. Современная математическая система обозначений является продуктом вековых усовершенствований, и принятые обозначения для высококачественной печати достаточно сложны. Например, переменные и буквы, обозначающие числа, сейчас обычно печатаются специальным математическим курсивом чуть отличным от обычного текстового курсива. Пробелы, окружающие символы операций такие как +, - ,× и /, немного отличаются от таковых в тексте, отражая соглашения о старшинстве оператора. Целые книги посвящены правилам набора математических текстов, от выравнивания верхних и нижних индексов до правил для выбора размеров круглых скобок и специальных нотационных соглашений для различных областей математики.
Принятая система обозначений в математике, и в печатном тексте вообще, направлена на то, чтобы зрительно выделить и сделать напечатанные выражения более легкими для чтения и понимания. Хотя это и кажется очевидным, но мы полагаемся на сотни соглашений таких как параграфы, заглавные буквы, семейства шрифтов, и даже механизм десятичной нумерации разделов, подобный тому, что мы используем в этом документе (заслуга G. Peano, который вероятно более известен своими аксиомами для натуральных чисел). Таким образом, нотационные соглашения, наверное, даже более важны для электронных медиа, где требуется бороться с трудностями чтения с экрана.
Однако, внедрение математики в Сеть это не просто поиск способов отображения математической информации в окне браузера. Сеть представляет фундаментально новый подход к хранению знаний, в котором взаимосвязь играет центральную роль. Становится все более и более важно найти способы взаимосвязи математических документов, которые облегчат автоматическую обработку, индексацию и повторное использование в других математических приложениях и контекстах. Подобные усовершенствования в технологии коммуникации позволяют расширить наши возможности в представлении и кодировании математического материала. Мы надеемся, что MathML является важным шагом в этом направлении.
Истоки и цели
История MathML
Задача представления математической информации для компьютерной обработки и электронных средств коммуникации возникла задолго до появления Интернета. Раньше общей практикой для ученых была запись статей в неком виде, основанном на ASCII-символах и дальнейшая пересылка их друг другу по электронной почте. Несколько языков математической разметки, в частности TEX, уже широко использовались в 1992 году, еще до того, как Сеть заняла столь значимое положение.
С самого начала Сеть зарекомендовала себя, как весьма эффективный способ сделать информацию доступной большому количеству людей. Однако, даже при том, что World Wide Web была изначально задумана и реализована учеными для ученых, возможности для включения математических выражений в HTML были крайне ограничены. В настоящее время, большая часть математической информации в Сети представлена в виде текста с графическими изображениями научных выражений (в формате GIF или JPEG) или в виде целых документов в формате PDF.
Консорциум World Wide Web (W3C) понимал, что отсутствие основ для научной коммуникации является серьезной проблемой. Уже в 1994 году Dave Raggett внес предложение о включении HTML Math в прототип HTML 3.0. На конференции в Дармштадте в апреле 1995 года был проведен круглый стол по математической разметке. В ноябре того же года представители Wolfram Research выдвинули предложение команде W3C о реализации поддержки математики в рамках HTML. Важную роль в объединении многих заинтересованных сторон сыграла проведенная в мае 1996 года встреча Digital Library Initiative в Champaign-Urbana. Результатом этой встречи стало формирование редакционного наблюдательного совета по HTML Math. Впоследствии эта рабочая группа разрослась, и в марте 1997 года была формально повторно сформирована как первая W3C Math Working Group. Вторая W3C Math Working Group была сформирована в июле 1998 года.
Проект MathML отражает интересы и мнения различных групп специалистов. Многое в развитии MathML заслуживает специального упоминания. Например, это касается вопроса общедоступности, где были особенно ощутимые затруднения. В этом направлении много работы проделал T. V. Raman. Neil Soiffer и Bruce Smith из Wolfram Research поделились своим опытом в решении проблем представления математического материала, накопленным при работе над проектом Mathematica 3.0. Их идеи оказали важное влияние на структуру элементов представления. Paul Topping из Design Science также внес свой вклад в математическое форматирование и редактирование. Много пользы извлек MathML из партнерства с рядом членов рабочих групп, связанных с другими работами по кодированию математической информации в SGML и в сообществах компьютерной алгебры. В их числе Stephen Buswell из Stilo Technologies, Nico Poppelier из Elsevier Science Stéphane Dalmas из INRIA (Sophia Antipolis), Stan Devitt из Waterloo Maple, Angel Diaz и Robert S. Sutor из IBM, и Stephen M. Watt из University of Western Ontario. Также, на MathML повлиял проект OpenMath, работа рабочей группы ISO 12083 и работа Stilo Technologies над фрагментом DTD для 'семантической' математики. Американское математическое общество играло ключевую роль в развитии MathML. Помимо прочего, председателями обеих W3C Math Working Group стали представители этой организации. С мая 1996 по март 1997 года группу вел Ron Whitney. Patrick Ion был сопредседателем группы с марта 1997 по июнь 1998 вместе с Robert Miner из The Geometry Center, а с июля 1998 вместе с Angel Diaz из IBM.
Ограниченность HTML
Спрос на эффективные средства обмена научной информацией остается по-прежнему высоким. Все больше и больше исследователей, ученых, инженеров, учителей, студентов, работая в различных местах земного шара, полагаются на электронные средства коммуникации. В тоже время, методы распространения научной нотации, основанные на графическом представлении, преобладающие сейчас в Сети, примитивны и неадекватны. Качество документов оставляет желать лучшего, создание - сложно, а математическая информация, содержащаяся в картинках, не доступна для поиска, индексации и повторного использования в других приложениях.
Существует две основных проблемы с использованием HTML.
Проблема отображения. Рассмотрим уравнение 22x=10. Размеры изображения подобраны так, чтобы соответствовать окружающему тексту размера 14 pt в системе, где оно было создано. Естественно, что в других системах или при другом размере текста уравнение будет выглядеть не так, как задумывал автор. Кроме того, изображение с этим уравнением создавалось в предположении, что у документа будет белый фон. Таким образом, если читатель или браузер установит другой цвет страницы, то в результате вокруг текста возникнет белый "ореол".
Далее рассмотрим уравнение
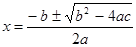 ,
,
которое служит примером выравнивания горизонтальной оси изображения по верху строчных букв в окружающем тексте. В этом уравнении присутствует знаменатель, и базисная линия располагается на расстоянии около одной трети от низа изображения. Это уравнение, например, можно разместить так:
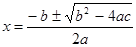 ,
,
то есть так, чтобы горизонтальная ось изображения и базисная линия уравнения совпадали, но это приведет к проблемам с межстрочными интервалами. В результате этого текст станет тяжело читаемым. Кроме того, вертикальное выравнивание по центру отличается в различных браузерах, делая невозможным гарантировать правильное расположение формул для различных пользователей.
Уравнения, оформленные в виде изображений, обычно труднее воспринимать, чем окружающий текст. Более того, эти проблемы только увеличиваются, если документ напечатать. Разрешение изображений около 70 точек на дюйм, тогда как окружающий текст обычно имеет 300, 600 или более точек. Такая разница в качестве неприемлема для большинства людей.
Проблемы кодирования. Попытаемся найти в этом документе фрагмент, например, '=10' первого уравнения выше. Или попробуем скопировать и вставить уравнение в другое приложение; более того, попробуем скопировать и вставить только фрагмент уравнения. При использовании методов, основанных на графическом представлении, ни одна из этих задач не может быть решена. И хотя использование атрибута alt в документе может немного помочь, ясно, что интерактивные web - документы должны предоставлять более продвинутый интерфейс между браузерами и математической информацией.
Другая проблема использования изображений для математических объектов - необходимость высокой пропускной способности канала связи. Представление уравнения разметкой обычно меньше по объему и лучше сжимаемо по сравнению с представлением в виде изображения. Кроме того, при использовании разметки для записи уравнений большая часть работы по отображению перекладывается на клиентскую машину.
Требования к математической разметке
Некоторые проблемы, связанные с включением математических выражений в HTML-документ в виде изображений, могут быть решены с помощью улучшения обработки последних браузерами. Хотя, даже если такое и произойдет, останется проблема доступа к информации, содержащейся в математических выражениях из других приложений. Поэтому, в будущем, улучшение методов, основанных на графическом представлении неперспективно. Для полной интеграции математического материала в web-документ необходимо представление математической нотации с помощью языка разметки.
При создании любого языка разметки необходимо тщательно учесть потребности его потенциальных пользователей. В случае с MathML область применения простирается от сферы образования до сферы исследований и даже бизнеса.
Сфера образования является большой и важной областью, в которой должна быть обеспечена возможность размещения в Сети научных материалов для занятий. В тоже время, преподаватели ограничены во времени и оборудовании, и обычно останавливаются перед сложностью создания технических web-документов. Студенты и преподаватели должны иметь возможность быстро и легко создавать математические документы, используя интуитивно понятные, легкие для изучения и "дешевые" инструменты.
Электронные учебники - другой способ использования Сети, который потенциально очень важен для образования. Известный специалист по управлению Peter Drucker прогнозировал конец эпохи построения системы высшего образования вокруг больших университетских городков и начало ее распространения через Сеть. Электронные учебники должны быть более интерактивными и позволять связывать текст с научным программным обеспечением.
Академические и коммерческие исследовательские группы постоянно выпускают большое количество научного материала. Все больше и больше научных публикаций размещается в базах данных, таких как довольно известный архив препринтов по физике и математике Национальной Лаборатории в Лос-Аламосе (Los Alamos). В особенности это относится к некоторым областям физики и математики, где цены на академические журналы весьма высоки. К тому же, базы данных с информацией о математических исследованиях, такие как Mathematical Reviews и Zentralblatt für Mathematik, предлагают огромное количество ссылок на содержащиеся в Сети математические документы.
Для соответствия требованиям исследовательского сообщества, язык математической разметки должен упростить обслуживание и работу с большими объемами документов, где крайне важны автоматический поиск и индексация. Из-за большого количества уже существующих математических документов, особенно в формате TEX, также немаловажно иметь возможность конвертации между существующими форматами и любым новым. И наконец, для научных исследований жизненно необходима возможность хранить информацию в архивах.
Многие ученые и инженеры используют в своей работе технические документы для обмена и записи результатов экспериментов, а также для компьютерного моделирования и проверки проведенных вычислений. Для такого рода использования методы размещения математической информации в Сети должны предоставлять стандартный способ совместного ее использования так, чтобы можно было легко ее прочитать, обработать и создавать с использованием доступных и простых инструментов.
Другое общее требование заключается в возможности отображения математического материала в других информационных средах, таких как речь или шрифт Брайля, которые крайне важны для людей с нарушением зрения.
Коммерческие издательства также заинтересованы в продвижении методов представления математической информации в Сети в различном виде от электронных версий обычных книг до интерактивных учебников и академических журналов. Издательствам требуется такой способ размещения математических документов в Сети, который бы имел возможность для высококачественного вывода, был применим для крупномасштабного коммерческого использования и, по возможности, совместим со старыми системами, в частности, на основе SGML.
Цели проекта MathML
Для соответствия различным требованиям научного сообщества MathML разрабатывался с учетом следующих условий.
MathML должен:
Представлять математический материал так, чтобы он подходил для обучения и научной коммуникации любого типа.
Представлять как математическую нотацию, так и математическое содержание.
Обеспечивать возможность преобразования между ним и другими математическим форматами, как презентационными, так и семантическими. Форматы вывода должны включать:
графическое отображение
синтезаторы речи
форматы систем компьютерной алгебры
форматы других языков, таких как TEX
отображение в виде простого текста, например, эмуляторы VT100
печатные устройства, включая работающие со шрифтом Брайля
Понятно, что такие преобразования могут привести к некоторой потере информации.
Иметь возможность включения информации, необходимой для определенных средств отображения и других приложений.
Поддерживать корректный просмотр длинных выражений.
Обеспечивать расширяемость.
Поддерживать шаблоны и другие средства редактирования математической информации.
Быть понятным человеку и простым для программной обработки.
В независимости от того, насколько удачен MathML как язык разметки, он будет полезен только в случае грамотного его применения. W3C Math Working Group определила короткий список дополнительных целей его реализации. В нем кратко описана минимальная функциональность, которую должны обеспечивать программы отображения и обработки MathML.
Выражения MathML внутри страниц HTML (и XHTML) должны корректно отображаться в наиболее распространенных браузерах в соответствии с установками читателя и автора, при этом должно обеспечиваться качество, максимально достижимое на данной платформе.
Документы HTML (и XHTML), содержащие выражения MathML, должны корректно выводиться на печать с высоким разрешением.
Выражения MathML, включенные в web-страницы, должны реагировать на действия пользователя, такие как работа с мышью, и осуществлять взаимодействие с другими приложениями через браузер.
Редакторы и конвертеры математических выражений должны разрабатываться с учетом возможности создавать web-страницы, содержащих выражения MathML.
В ближайшее время для решения проблемы отображения планируется использовать встраиваемые элементы, такие как Java-апплеты, плагины и элементы управления ActiveX. Однако объем, в котором будет это реализовано, зависит от сотрудничества и поддержки производителей браузеров и другого програмного обеспечения. W3C Math Working Group продолжает работу с рабочими группами по Document Object Model (DOM) и Extensible Style Language (XSL), чтобы гарантировать, что нужды научного сообщества будут удовлетворены в будущем. Ясно, что MathML 2.0 является значительным шагом вперед по сравнению с MathML 1.0 Recommendation (Апрель 1998).
Роль MathML в Сети
Цели разработки MathML требуют гибкой и расширяемой системы записи математического материала, позволяющей взаимодействовать с внешними программами и осуществлять высококачественное отображение в различных информационных средах. Но любой язык разметки, удовлетворяющий всем этим требованиям, достаточно сложен.
В то же время, для многих групп пользователей, например, студентов, важно иметь простой путь для включения математических выражений в web-страницы. Аналогично, для других групп, например, для пользователей системы TEX, лучшим решением была бы система, позволяющая непосредственное включение в web-страницы разметки при помощи языка, подобного TEX. В общем, различным группам пользователей требуются различные формы ввода и вывода информации, наиболее соответствующие их потребностям. Следовательно, в идеале система для размещения математических документов в Сети должна предоставлять как специализированные сервисы для ввода и вывода, так и общие сервисы для обмена информацией и отображения в различных информационных средах.
На практике, обзор того, что должен обеспечивать математический стандарт в сети для специализированных и общих нужд, приводит к идее многоуровневой архитектуры. Первый уровень включает стандартные мощные средства обмена, обработки и отображения математических данных. Второй уровень включает специализированные инструменты, предназначенные для конкретных групп пользователей, с помощью которых можно легко кодировать математическую информацию для ее распространения среди ограниченного круга пользователей.
MathML создан для разметки математической информации на нижнем более общем уровнем двухуровневой архитектуры. Это предполагает разметку сложной нотационной и семантической структуры в строгой, регулярной форме, простой для обработки средствами отображения, поиска и индексации, а также другими математическими приложениями.
Вследствие этого, разметка MathML не предполагает непосредственного использования авторами. MathML понятен для человека, что сильно помогает при отладке, но во всех случаях, за исключением простейших, он слишком сложен для ручного кодирования. Вместо этого авторы должны будут использовать специальные редакторы формул, конвертеры и другие специализированные программные средства для создания документов MathML. В качестве альтернативы, некоторые программы отображения и системы поддержки математических документов могут преобразовывать другие входные форматы в MathML "на лету".
В некотором смысле MathML аналогичен другим низкоуровневым коммуникативным форматам, таким как язык PostScript, разработанный Adobe. Вы можете создавать PostScript-файлы различными способами, в зависимости от ваших потребностей: эксперты создают и правят их вручную, авторы создают их с помощью текстовых процессоров, дизайнеры - программами-иллюстраторами и так далее. Если у вас есть PostScript-файл, вы можете распространить его среди очень большой аудитории, так как устройства отображения PostScript, такие как принтеры и программы для просмотра на экране, широко доступны.
Одной из причин разработки MathML как языка разметки общего коммуникативного уровня является стимулирование разработки математического программного обеспечения Сети верхнего уровня. MathML представляет способ координирования усилий разработчиков модулей программ для создания и отображения математического материала. Упрощая разработку функциональных частей большой системы, MathML может стимулировать разработку программ, которые будут очень полезны потенциальным пользователям.
Авторы могут создавать MathML-документы, используя инструменты, лучше подходящие для их нужд. Студенты могут предпочитать визуальные редакторы формул, с возможностью сохранять блоки разметки MathML в XHTML-файле. Исследователи могут использовать пакеты компьютерной алгебры, автоматически кодирующие математическую информацию так, чтобы коллеги могли ее взять из web-страницы и обработать. Издатели академических журналов могут использовать программу, которая конвертирует разметку TEX в HTML и MathML. Независимо от метода создания web-страницы, содержащей MathML, становятся доступны все преимущества общего коммуникативного слоя. Различные программы, работающие с MathML, могут быть использованы для одного и того же документа, чтобы вывести его в систему воспроизведения речи и на печать, а также для ввода в систему компьютерной алгебры и для управления им как частью большого архива web-документов. Для высококачественной печати математических документов в формате MathML часто проводится обратная конвертация в стандартные системы верстки, включая TEX, который специально создан для этих целей. Наконец, можно ожидать, что в конечном счете MathML будет интегрирован в другие области, где встречаются математические формулы, такие как электронные таблицы, пакеты статистической обработки данных и средства инженерной разработки.
W3C Math Working Group сотрудничает с различными софтверными компаниями для гарантии того, что скоро появятся различные программы для работы с MathML, включая как средства создания документов, так и их отображения. Текущий список программ, работающих с MathML расположен на странице Math World Wide Web Consortium.
Первоначальная концепция HTML Math состояла в том, чтобы просто расширить набор тэгов HTML и таким образом обеспечить непосредственную интерпретацию в браузере. Однако еще до этого лавинообразный рост сети сделал понятным, что требуется глобальный механизм расширений, а математическая информация является только одним из типов структурированных данных, которые могут быть интегрированы в Сеть с помощью такого механизма.
При условии, что MathML должен интегрироваться в Сеть в качестве расширения, очень важно, чтобы MathML и использующие его программы могли хорошо взаимодействовать с существующей web-средой. В частности, MathML должен разрабатываться с учетом трех типов взаимодействия. Во-первых, для создания математического контента важно, чтобы существующие языки математической разметки могли быть преобразованы в MathML, и чтобы в существующие редакторы была добавлена возможность создания документов MathML. Во-вторых, должно обеспечиваться возможность вставлять разметку MathML в разметку HTML, как ее дополнение, в этом случае, в будущем, она будет доступна для браузеров, поисковых систем и всех типов web-приложений, которые сейчас работают с HTML. И, наконец, должна обеспечиваться возможность отображения MathML, встроенного в HTML, современными браузерами, даже если результат будет далек от идеала. С переходом от HTML к XHTML все вышеперечисленные требования станут еще более необходимыми.
World Wide Web полностью интернационален. Математика - язык, использующийся во всем мире. Математическая нотация в науке и технике тесно связана с национальными языками. W3C стремится быть конструктивной силой в распространении коммуникативных возможностей в мире. Поэтому разработчики MathML столкнулись с проблемой интернационализации. Неизвестно о несовместимости этой версии MathML с языками с написанием слева направо. Запись слева направо является стандартной в MathML 2, и понятно, что потребность в записи математических формул в текстах на некоторых национальных языках еще не возникала. Так называемая "двунаправленная технология" только разрабатывается, и лучшая поддержка формул в этом контексте - задача будущих разработок.
Дата: 2019-04-23, просмотров: 325.