Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Стационарное распределение представимо в форме произведения множителей характеризующих узлы; каждый множитель есть стационарное распределение узла, то есть

 

.

 

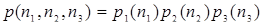Стационарное распределение 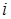-ого узла имеет вид

 

,

 

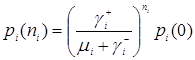где

 

, .

 

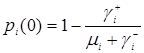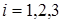Таким образом, стационарное распределение имеет следующий вид

 

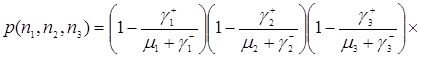
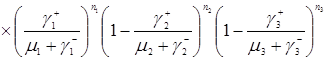. (3.4.1)

 

Обозначим через

 

, , .

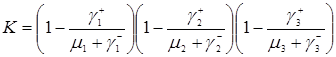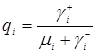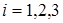Тогда в этих обозначениях формула (3.4.1) запишется в следующем виде

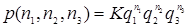.                                (3.4.2)

 

Подставляя формулу (3.4.2) в уравнения равновесия (3.3.1), получим

 

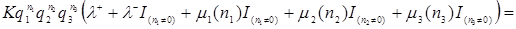
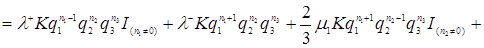
 (3.4.3)

.

 

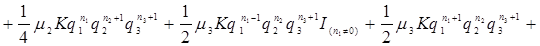
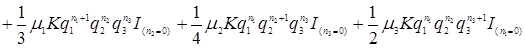Разделим обе части уравнения (3.4.3) на 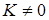, получим

 

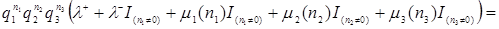
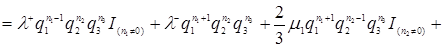
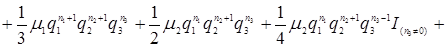
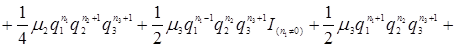 (3.4.4)

.

 

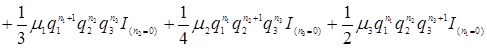Через 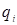 запишем уравнения трафика (3.1.12) – (3.1.17)

 

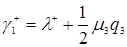,                 (3.4.5)

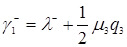,                                             (3.4.6)

,                                                    (3.4.7)

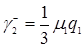,                                   (3.4.8)

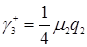,                                              (3.4.9)

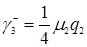.                                                        (3.4.10)

Так как , ( 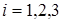), то получим следующие соотношения        

 

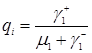,                                                            (3.4.11)

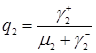,                                                           (3.4.12)

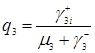.                                                            (3.4.13)

 

Рассмотрим всевозможные случаи числа заявок в марковской модели сети с тремя узлами и разнотипными заявками. То есть следующие случаи

 

1) , , ;

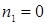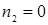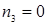2) , , ;

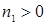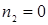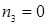3) , , ;

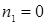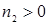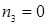4) , , ;

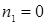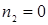5) , , ;

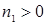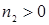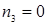6) , , ;

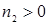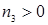7) , , ;

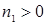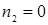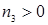8) , , ;

 

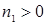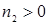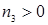Подставляя значения  в уравнение (3.4.4), учитывая уравнения (3.4.5) – (3.4.13), проверим, удовлетворяет стационарное распределение (3.4.1) уравнениям равновесия (3.3.1). Рассмотрим каждый из случаев 1) – 8) отдельно.

Рассмотрим первый случай , ,

 

.

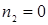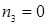
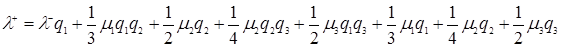Согласно формуле (3.4.6) 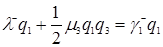, формуле (3.4.8) 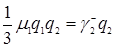, , 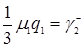формуле (3.4.10) 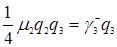, формуле (3.4.9) 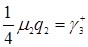, получим

,

.

 

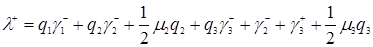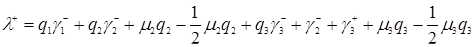В соответствии с формулой (3.4.5) 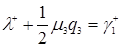, формулой (3.4.12) 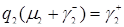, формулой (3.4.13) 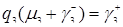. Из формул (3.4.9), (3.4.10) 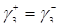, тогда имеем

 

,

.

 

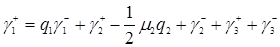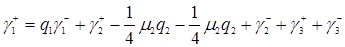Согласно формуле (3.4.9) 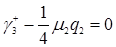, формуле (3.4.10) 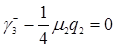. Из формул (3.4.7) и (3.4.8) 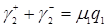, получим

 

,

.

 

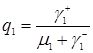А это есть формула (3.4.11), то есть случай 1) выполняется.

Рассмотрим второй случай , ,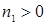

,

 

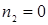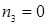
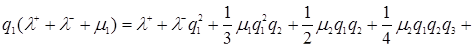
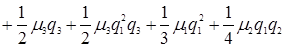Согласно формуле (3.4.5) 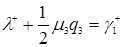, формуле (3.4.6) 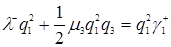, формуле (3.4.8) 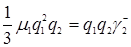, , 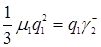формуле (3.4.10) 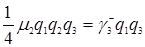, формуле (3.4.10) 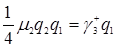. Из формул (3.4.5) и (3.4.6) 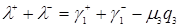. Раскроем скобки и перенесём всё в правую часть, получим

 

.

 

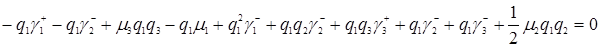В соответствии с формулой (3.4.13) 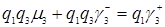, формулой (3.4.12). Из формул (3.4.9), (3.4.10) 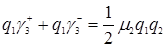, тогда

 

.

 

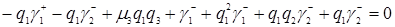Согласно формуле (3.4.11) 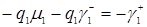, ,формуле (3.4.12) 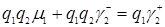. Из формул (3.4.7) и (3.4.8) 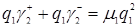, получим

 

.

 

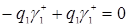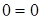, то есть случай 2) выполняется.

Аналогично выполняются 3) – 8).

Таким образом, случаи 1) – 8) превращаются в верное равенство. То есть стационарное распределение (3.4.1) есть решение уравнения равновесия (3.3.1), если выполняется условие эргодичности , .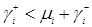

 

ЗАКЛЮЧЕНИЕ

 

В работе проведено исследование открытых марковских и полумарковских сетей массового обслуживания с тремя узлами и циклической маршрутизацией.

Получены следующие основные результаты:

Для марковской модели сети с тремя узлами, записаны уравнения равновесия (формула 1.1.3), получено достаточное условие эргодичности (формула 1.3.1) и найдено стационарное распределение (формула 1.2.9).

Для полумарковской модели сети с тремя узлами, определен вид дифференциально-разностных уравнений Колмогорова (формула 2.1.4), найдено стационарное распределение (формула 2.2.1) и доказана инвариантность (см. 2.3).

Для марковской модели сети с тремя узлами и разнотипными заявками, составлены уравнения равновесия (формула 3.3.1), найдено стационарное распределение (формула 3.4.1) и получено достаточное условие эргодичности (формула 3.2.15).

Результаты работы могут быть применены при проектировании и эксплуатации сетей передачи данных, информационно-вычислительных сетей, сетей ЭВМ и многих других технических объектов.