 Рассмотрим изолированный
Рассмотрим изолированный 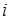 -й узел (
-й узел ( 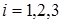 ), считая, что на него поступает поток заявок интенсивности
), считая, что на него поступает поток заявок интенсивности 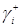 . Граф переходов изобразится следующим образом.
. Граф переходов изобразится следующим образом.
 |


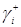
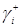
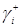
 | |||||
 | |||||
 | |||||







 0 1 2 …
0 1 2 … 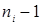
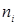 …
…
 | |||||||
 | |||||||
 | |||||||
 | |||||||
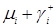
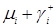
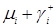
Рисунок 3.1.1
Тогда в соответствии с рисунком 3.1.1, получим следующие соотношения
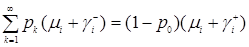 ,
, 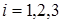 , (3.1.1)
, (3.1.1)
где 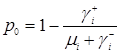 .
.
Согласно рисунку 3.1
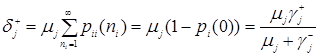 ,
, 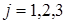 . (3.1.2)
. (3.1.2)
Для марковской модели сети с тремя узлами и разнотипными заявками уравнения трафика имеют следующий вид:
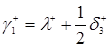 ,
,
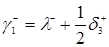 ,
,
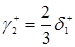 ,
,
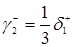 ,
,
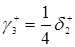 ,
,
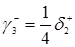 .
.
Учитывая формулу (3.1.2) запишем ещё три уравнения
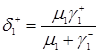 ,
,
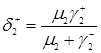 ,
,
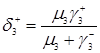 .
.
Таким образом, уравнения трафика имеют следующий вид
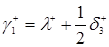 . (3.1.3)
. (3.1.3)
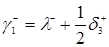 , (3.1.4)
, (3.1.4)
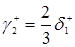 , (3.1.5)
, (3.1.5)
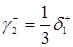 , (3.1.6)
, (3.1.6)
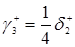 , (3.1.7)
, (3.1.7)
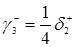 , (3.1.8)
, (3.1.8)
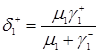 , (3.1.9)
, (3.1.9)
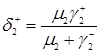 , (3.1.10)
, (3.1.10)
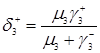 , (3.1.11)
, (3.1.11)
Подставим формулу (3.1.9) в (3.1.5) и (3.1.6), формулу (3.1.10) в (3.1.7) и (3.1.8), а формулу (3.1.11) в (3.1.3) и (3.1.4). Тогда уравнения трафика запишутся следующим образом
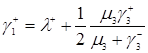 , (3.1.12)
, (3.1.12)
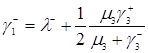 , (3.1.13)
, (3.1.13)
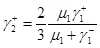 , (3.1.14)
, (3.1.14)
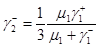 , (3.1.15)
, (3.1.15)
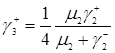 , (3.1.16)
, (3.1.16)
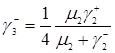 . (3.1.17)
. (3.1.17)
Нахождение решений уравнений трафика
Положительность решения уравнений трафика для достаточно общей модели доказана в работе [9].
Для нахождения решений уравнений трафика составим уравнение относительно 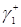 . Для этого преобразуем формулу (3.1.12), перенесём всё в левую часть и приведём к общему знаменателю
. Для этого преобразуем формулу (3.1.12), перенесём всё в левую часть и приведём к общему знаменателю
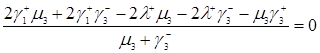 . (3.2.1)
. (3.2.1)
Так как 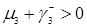 , то формула (3.2.1) примет следующий вид
, то формула (3.2.1) примет следующий вид
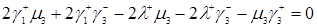 . (3.2.2)
. (3.2.2)
Подставляя формулу (3.1.14) и (3.1.15) в (3.1.16) имеем
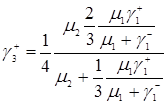 .
.
Приводим к общему знаменателю
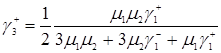 . (3.2.3)
. (3.2.3)
Подставим формулу, полученную из формулы (3.1.13) вычетом формулы (3.1.12), получим 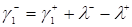 , в формулу (3.2.3), получим
, в формулу (3.2.3), получим
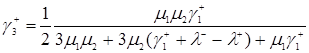 ,
,
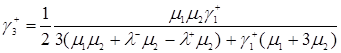 . (3.2.4)
. (3.2.4)
Обозначим 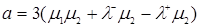 и
и 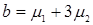 , тогда
, тогда
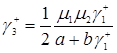 . (3.2.5)
. (3.2.5)
В соответствии с формулами (3.1.16) и (3.1.17)
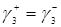 . (3.2.6)
. (3.2.6)
Учитывая формулу (3.2.6) и (3.2.5), получим
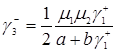 . (3.2.7)
. (3.2.7)
Подставим формулы (3.2.5) и (3.2.6) в формулу (3.2.2), имеем
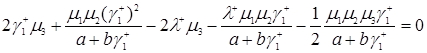 . (3.2.8)
. (3.2.8)
Так как 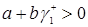 , то формула (3.2.8) примет следующий вид
, то формула (3.2.8) примет следующий вид
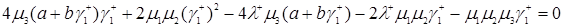 . (3.2.9)
. (3.2.9)
Раскрывая скобки и приводя подобные члены, запишем формулу (3.2.9) в виде
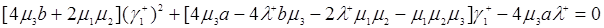 (3.2.10)
(3.2.10)
Таким образом, полученное уравнение (3.2.10) квадратное, то есть
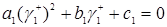 , (3.2.11)
, (3.2.11)
где коэффициенты 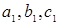 , учитывая обозначения
, учитывая обозначения 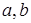 и формулу (3.2.10), определяются следующим образом
и формулу (3.2.10), определяются следующим образом
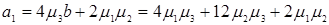 , (3.2.12)
, (3.2.12)
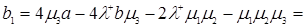
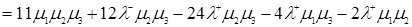 , (3.2.13)
, (3.2.13)
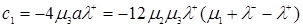 . (3.2.14)
. (3.2.14)
Для уравнения (3.2.11) найдём дискриминант, учитывая формулы (3.2.12), (3.2.13), (3.2.14), имеем
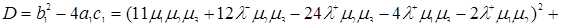
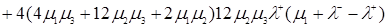 .
.
Для получения решения уравнения (3.2.11) должно выполнятся следующее условие 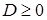 , а это возможно тогда, когда
, а это возможно тогда, когда
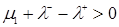 .
.
Согласно формуле 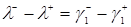 , получим
, получим
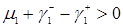 ,
,
то есть
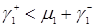 . (3.2.15)
. (3.2.15)
В соответствии с рисунком 3.1, формула (3.2.15) есть условие эргодичности. Если это условие не выполняется, то нет стационарного распределения.
Учитывая формулы (3.2.12), (3.2.14), (3.2.15) получим, что 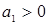 ,
, 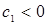 . Согласно обратной теореме Виета, если
. Согласно обратной теореме Виета, если 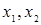 - корни уравнения (3.2.11), то выполняются следующие соотношения
- корни уравнения (3.2.11), то выполняются следующие соотношения
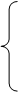
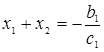
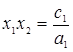
Так как 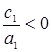 , то один из корней положительный и один отрицательный.
, то один из корней положительный и один отрицательный.
Таким образом, уравнение (3.2.11) имеет одно положительное решение. То есть система уравнений трафика (3.1.12) – (3.1.17) имеет положительное решение.
Уравнения равновесия
В соответствии, с рисунком 3.1 составим уравнения равновесия
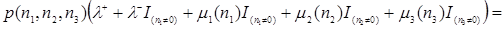
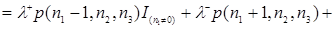
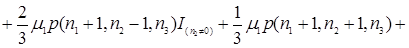
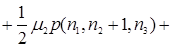
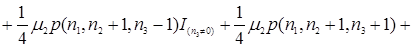
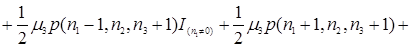
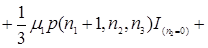
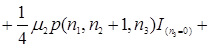 (3.3.1)
(3.3.1)
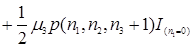 .
.
Дата: 2019-05-28, просмотров: 316.