Теория.
При использовании катушек индуктивности на низких частотах возникает множество неудобств, поэтому разработаны схемы, лишенные этих элементов. Рассмотрим схему фильтра, получаемую из лестничной 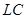 -структуры заменой катушек индуктивности на гираторы, в качестве нагрузки которых используется емкостное сопротивление. Гиратором называется устройство, преобразующее импеданс. В частности, гиратор, нагруженный на емкость, ведет себя на входных зажимах как индуктивность. Схема гиратора представлена как Схема 4.
-структуры заменой катушек индуктивности на гираторы, в качестве нагрузки которых используется емкостное сопротивление. Гиратором называется устройство, преобразующее импеданс. В частности, гиратор, нагруженный на емкость, ведет себя на входных зажимах как индуктивность. Схема гиратора представлена как Схема 4.
Схема 4. Гиратор.
Гирпторные схемы являются разновидностью активных  -фильтров (
-фильтров (  -фильтров) и часто носят название активных лестничных фильтров (АЛФ). Основное соотношение гиратора:
-фильтров) и часто носят название активных лестничных фильтров (АЛФ). Основное соотношение гиратора:
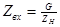 , (3.2)
, (3.2)
где 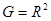 - коэффициент гирации;
- коэффициент гирации; 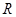 - сопротивление, используемое в схеме гиратора.
- сопротивление, используемое в схеме гиратора.
В частности, если 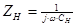 , то получим из (3.2)
, то получим из (3.2) 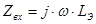 , где
, где 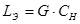 .
.
На рисунке 3.6[10] представлены основные преобразования индуктивностей, включенных в последовательные и параллельные ветви,  - и
- и  -образных звеньев индуктивностей
-образных звеньев индуктивностей  -структур. Такие преобразования позволяют составить схему АЛФ с наименьшим числом гираторов.
-структур. Такие преобразования позволяют составить схему АЛФ с наименьшим числом гираторов.
Порядок расчета АЛФ следующий:
1. составить схему АЛФ на основе схемы 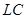 -фильтра, рассчитанной ранее;
-фильтра, рассчитанной ранее;
2. найти емкости, полученные преобразованием соответствующих индуктивностей, по формуле 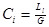 . Коэффициент гирации подбирается таким, чтобы получающиеся значения емкостей были одного порядка со значениями емкостных элементов, уже использованными в лестничной
. Коэффициент гирации подбирается таким, чтобы получающиеся значения емкостей были одного порядка со значениями емкостных элементов, уже использованными в лестничной  -структуре.
-структуре.
Расчет.
Используя одну из схем замещения на рисунке 3.6.
Схема 5. Схема замещения.
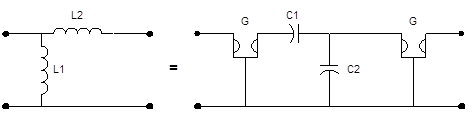
Составим схему АЛФ на основе 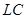 -фильтра.
-фильтра.
Схема 6. Гираторная реализация безиндуктивного фильтра.
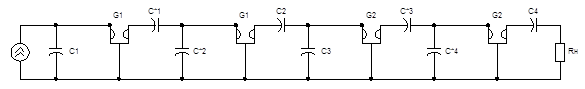
Уменьшим заданные частоты на порядок, то есть 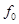 = 1000 [Гц],
= 1000 [Гц], 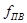 = 1200 [Гц],
= 1200 [Гц], 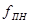 = 833 [Гц],
= 833 [Гц], 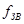 = 1500 [Гц],
= 1500 [Гц], 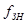 = 667 [Гц]. И пересчитаем значения элементов для новых частот:
= 667 [Гц]. И пересчитаем значения элементов для новых частот:
| Номер, i | 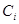 , [мкФ] , [мкФ]
| 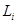 , [мГн] , [мГн]
|
| 1 | 14.01 | 1.808 |
| 2 | 0.753 | 33.64 |
| 3 | 13.98 | 1.812 |
| 4 | 1.396 | 18.14 |
Теперь найдем емкости, полученные преобразованием соответствующих индуктивностей, по формуле 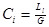 . Пусть
. Пусть 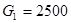 и
и 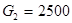 , тогда элементная база схемы будет выглядеть следующим образом:
, тогда элементная база схемы будет выглядеть следующим образом: 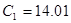 [мкФ],
[мкФ], 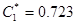 [мкФ],
[мкФ], 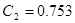 [мкФ],
[мкФ],  [мкФ],
[мкФ], 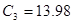 [мкФ],
[мкФ], 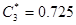 [мкФ],
[мкФ], 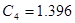 [мкФ],
[мкФ], 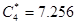 [мкФ].
[мкФ].
 -фильтр с каскадной структурой.
-фильтр с каскадной структурой.
Теория.
Подход к реализации  -фильтра, собираемого из звеньев первого и второго порядка, аналогичен тому способу построения фильтра, который был описан при реализации
-фильтра, собираемого из звеньев первого и второго порядка, аналогичен тому способу построения фильтра, который был описан при реализации 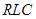 -звеньев.
-звеньев. 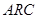 -звенья строятся без использования индуктивностей. Звено представляет собой соединение одного, двух или трех операционных усилителей (ОУ) с резистивно-емкостной цепью. Применение обратных связей позволяет реализовывать все возможные конфигурации действительных и комплексных нулей и полюсов. Перед тем как приступить к расчету звеньев, необходимо разбить передаточную функцию, полученную на этапе аппроксимации, на сомножители. Тем самым нули и полюсы будут поделены на группы, поддающиеся реализации с помощью звеньев первого и второго порядка. Примеры группирования нулей и полюсов даны на рисунке 3.4.[11] Конкретные схемы, диаграммы полюсов и нулей, соответствующие им, а также расчетные соотношения можно отыскать в таблице 3.5.[12]
-звенья строятся без использования индуктивностей. Звено представляет собой соединение одного, двух или трех операционных усилителей (ОУ) с резистивно-емкостной цепью. Применение обратных связей позволяет реализовывать все возможные конфигурации действительных и комплексных нулей и полюсов. Перед тем как приступить к расчету звеньев, необходимо разбить передаточную функцию, полученную на этапе аппроксимации, на сомножители. Тем самым нули и полюсы будут поделены на группы, поддающиеся реализации с помощью звеньев первого и второго порядка. Примеры группирования нулей и полюсов даны на рисунке 3.4.[11] Конкретные схемы, диаграммы полюсов и нулей, соответствующие им, а также расчетные соотношения можно отыскать в таблице 3.5.[12]
При расчете следует иметь в виду:
1. Выбор той или иной схемы, включаемой в каскадное соединение, определяется диаграммой нулей и полюсов синтезируемого фильтра. Возможно, также ориентироваться на вид передаточной функции звена.
2. Звенья на одном операционном усилителе предназначены для реализации полюсов с невысокими добротностями. Добротность полюса вычисляется по формуле 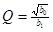 . Если
. Если 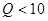 , то можно использовать простые схемы типа 3…7. При
, то можно использовать простые схемы типа 3…7. При  следует применять более сложные схемы типа 8…12.
следует применять более сложные схемы типа 8…12.
3. 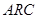 -схемы сочетать фильтрацию с усилением. Заданный коэффициент усиления следует распределить по каскадам так, чтобы
-схемы сочетать фильтрацию с усилением. Заданный коэффициент усиления следует распределить по каскадам так, чтобы 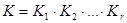 , где
, где 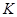 - общий коэффициент усиления,
- общий коэффициент усиления, 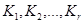 - коэффициент усиления каскадов.
- коэффициент усиления каскадов.
4. После расчета элементов звеньев нужно выбрать номинальные значения, наиболее близкие к вычисленным, и, кроме того, подобрать конкретный тип микросхемы ОУ.
Предлагаемый расчет 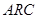 -звеньев упрощенный. С более сложной методикой, включающей в себя оценку нестабильности характеристик фильтра, расчет нелинейных искажений и допустимого динамического диапазона, можно ознакомится в дополнительной литературе.
-звеньев упрощенный. С более сложной методикой, включающей в себя оценку нестабильности характеристик фильтра, расчет нелинейных искажений и допустимого динамического диапазона, можно ознакомится в дополнительной литературе.
Порядок включения каскадов тоже важен. Нужно, чтобы перед звеном, имеющим всплеск АЧХ на некоторой частоте, стояло звено, обладающее на этой частоте небольшим значение АЧХ. Это достигается включением каскадов друг за другом в порядке увеличения добротности реализуемых полюсов.
Расчет.
Итак, обратимся к таблице 3.5 и выберем нужный нам вариант схем:
| Схема и диаграмма нулей и полюсов. | Передаточная функция | Расчет |

| 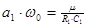
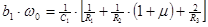
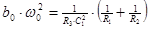
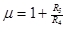
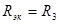
| 1.  2.
2. 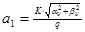 , где , где 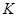 - коэффициент усиления звена, - коэффициент усиления звена, 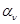 и и 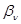 - координаты полюса ФНЧ-прототипа, - координаты полюса ФНЧ-прототипа, 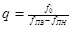 3. Выбор
3. Выбор 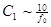 [мкФ]
4. [мкФ]
4. 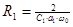 5.
5. 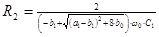 6.
6. 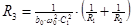 7.
7. 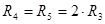
|
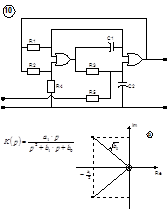
| 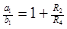
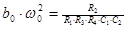
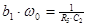
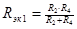
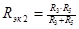
| 1. 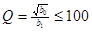 2.
2. 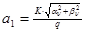 , где , где 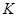 - коэффициент усиления звена, - коэффициент усиления звена, 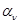 и и 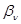 - координаты полюса ФНЧ-прототипа, - координаты полюса ФНЧ-прототипа, 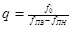 3. Выбор
3. Выбор 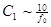 [мкФ]
4. [мкФ]
4. 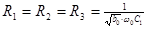 5.
5. 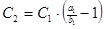 6.
6. 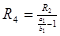 7.
7. 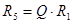
|
Уменьшим заданные частоты на порядок, то есть 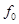 = 1000 [Гц],
= 1000 [Гц], 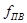 = 1200 [Гц],
= 1200 [Гц], 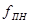 = 833 [Гц],
= 833 [Гц], 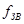 = 1500 [Гц],
= 1500 [Гц], 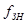 = 667 [Гц].
= 667 [Гц].
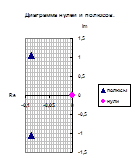
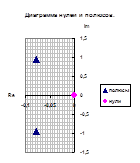
Сгруппируем нули и полюсы, отталкиваясь от диаграммы нулей и полюсов ППФ:
| Первый каскад | Второй каскад | Третий каскад | Четвертый каскад |
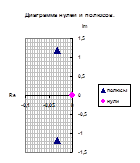
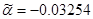 , , 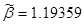
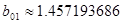

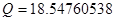
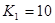
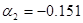 , , 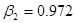
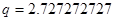
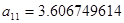
| 
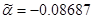 , , 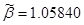
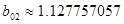
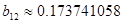
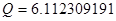
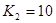
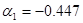 , , 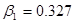
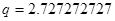
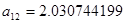
| 
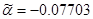 , , 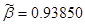
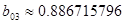
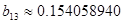
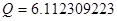

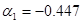 , , 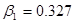
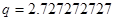
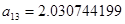
| 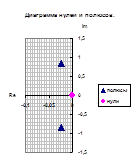
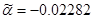 , , 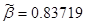
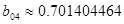
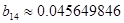
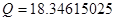
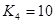
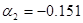 , , 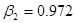
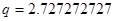
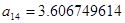
|
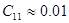 [мкФ] [мкФ]
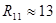 [кОм] [кОм]
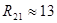 [кОм] [кОм]
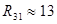 [кОм] [кОм]
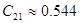 [мкФ] [мкФ]
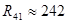 [Ом] [Ом]
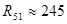 [кОм] [кОм]
| 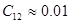 [мкФ] [мкФ]
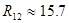 [кОм] [кОм]
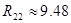 [кОм] [кОм]
 [кОм] [кОм]
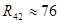 [кОм] [кОм]

|  [мкФ] [мкФ]
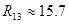 [кОм] [кОм]
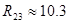 [кОм] [кОм]
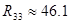 [кОм] [кОм]
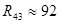 [кОм] [кОм]
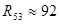 [кОм] [кОм]
| 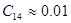 [мкФ] [мкФ]
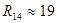 [кОм] [кОм]
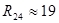 [кОм] [кОм]
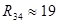 [кОм] [кОм]
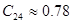 [мкФ] [мкФ]
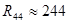 [Ом] [Ом]
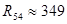 [кОм] [кОм]
|
Запишем передаточную функцию, исходя из диаграмм нулей и полюсов.
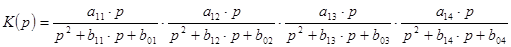
А теперь найдем принципиальную схему для реализации 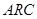 -фильтра.
-фильтра.
Схема 7. Схема ARC-реализации.

Дата: 2019-05-28, просмотров: 291.