Курсовая работа
на тему
| Синтез частотно-избирательного фильтра. |
| Выполнил: | студент группы ##-### Гуренков Дмитрий |
| Проверил: | преподаватель Ручьев М. К. |
Москва 2011 г.
Содержание
Задание................................................................................................................................................................................. 3
Исходные данные...................................................................................................................................................... 3
Аппроксимация частотной характеристики фильтра............................................................ 4
Последовательность шагов....................................................................................................................................... 4
Тип фильтра........................................................................................................................................................................ 4
Требования к ФНЧ-прототипу.................................................................................................................................... 4
Порядок, нули и полюсы ФНЧ-прототипа............................................................................................................ 5
Нули и полюсы синтезируемого фильтра........................................................................................................... 5
Передаточная функция и АЧХ................................................................................................................................... 6
Расчет................................................................................................................................................................................... 6
Реализация аналогового фильтра............................................................................................................. 9
Лестничная 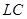 - структура....................................................................................................................................... 9
- структура....................................................................................................................................... 9
Теория................................................................................................................................................................................ 9
Расчет............................................................................................................................................................................. 10
Каскадное соединение 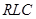 - звеньев............................................................................................................. 11
- звеньев............................................................................................................. 11
Теория............................................................................................................................................................................. 11
Расчет............................................................................................................................................................................. 12
Гираторная реализация безиндуктивного фильтра...................................................................................... 13
Теория............................................................................................................................................................................. 13
Расчет............................................................................................................................................................................. 14
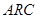 -фильтр с каскадной структурой............................................................................................................... 14
-фильтр с каскадной структурой............................................................................................................... 14
Теория............................................................................................................................................................................. 14
Расчет............................................................................................................................................................................. 15
Сравнительная характеристика различных реализаций синтезируемого фильтра. 17
Литература..................................................................................................................................................................... 18
Задание
1. Представить данные на синтез частотно-избирательного фильтра в графической форме с использованием нормированной частоты 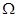 .
.
2. Определить технические требования к нормированному ФНЧ прототипу: тип и порядок фильтра.
3. Найти координаты нулей и полюсов нормированной передаточной функции ФНЧ прототипа.
4. Найти лестничную структуру ФНЧ прототипа с нормированными элементами.
5. Определить координаты нулей и полюсов передаточной функции синтезируемого частотно-избирательного фильтра. Построить график АЧХ с использованием денормированной частоты 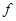 .
.
6. Определить лестничную структуру синтезируемого фильтра с нормированными элементами и провести денормирование элементов.
7. Выбрать возможные варианты RLC-звеньев первого и второго порядков, предназначенных для каскадной реализации фильтра, рассчитать величины элементов и составить полную схему фильтра.
8. Уменьшив частотные параметры на два порядка:
8.a. Составить схему и провести расчет элементов для гираторной реализации фильтра.
8.b. Выбрать возможные варианты ARC-звеньев первого и второго порядков, предназначенные для безиндукционной каскадной реализации фильтра, рассчитать величины элементов и составить полную схему фильтра.
9. Сделать вывод, дав сравнительную характеристику различным вариантам реализации синтезируемого фильтра.
Исходные данные
Задача синтеза фильтра состоит в разработке электрической схемы устройства, обладающего требуемыми частотными и временными характеристиками. Курсовая работа предполагает проектирование фильтра на основе требования к форме его характеристики затухания. При синтезе полосно-пропускающего фильтра вводится требование к верхним и нижним граничным частотам полосы пропускания ( 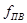 ,
, 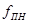 ,
, 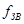 ,
, 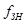 ).
).
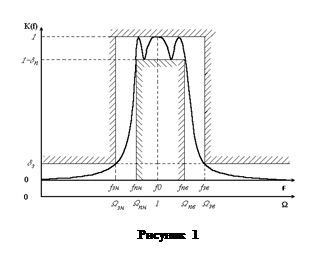 Амплитудно-частотная характеристика (АЧХ) фильтра
Амплитудно-частотная характеристика (АЧХ) фильтра 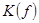 и характеристика затухания
и характеристика затухания 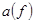 связаны друг с другом выражением
связаны друг с другом выражением
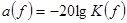 ,
,
поэтому при рассмотрении требований к АЧХ необходимо вместо допусков 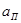 и
и 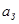 ввести параметры:
ввести параметры: 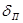 - допустимую неравномерность в полосе пропускания и
- допустимую неравномерность в полосе пропускания и 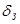 - максимально допустимую передачу в полосе задержания, причем
- максимально допустимую передачу в полосе задержания, причем
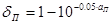 ,
, 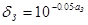 .
.
Типичная АЧХ полосно-пропускного фильтра Чебышева приведена на рисунке.
Процедура проектирования частотно-избирательного фильтра включает в себя два основных этапа:
1. Этап проектирования, в ходе которого подбирается передаточная функция, удовлетворяющая заданным требованиям (АЧХ, выделенная из аппроксимирующей передаточной функции, не должна выходить за пределы заданного коридора допусков);
2. Этап реализации, суть которого – в выборе принципа реализации передаточной функции, разработке и расчете конкретной схемы фильтра, обладающего найденной передаточной функцией.
Порядок выполнения первого этапа достаточно хорошо разработан, поставленная задача решается с использованием какого-либо из многочисленных справочников по расчету фильтров. Решение второй задачи в рамках второго этапа многовариантно. Это связано с тем, что известно довольно много принципов и схем, позволяющих реализовать найденную передаточную функцию.
Последовательность шагов
На этапе аппроксимации необходимо проделать следующее:
1. Выбрать тип фильтра.
2. Пересчитать исходные данные в требования к фильтру – прототипу нижних частот (ФНЧ-прототипу).
3. Определить минимальный порядок ФНЧ-прототипа, нули и полюсы его передаточной функции (с помощью справочника).
4. Пересчитать нули и полюса ФНЧ-прототипа в нули и полюсы синтезируемого фильтра.
5. Записать передаточную функцию фильтра, найти и построить АЧХ или характеристику затухания.
Тип фильтра
Существует ряд типов фильтров, различающихся по характеру их передаточных функций. Например, фильтр Баттерворта, фильтр Чебышева, эллиптический (Золоторева - Каура) фильтр. Каждый из указанных типов в определенном смысле оптимален. Главная же особенность состоит в том, что заданную избирательность фильтр Чебышева обеспечивает при меньшем порядке, чем фильтр Баттерворта, а эллиптический фильтр в этом смысле лучше чебышевского.
Требования к ФНЧ-прототипу
Для того чтобы не было привязки начального этапа расчета к конкретным значениям частоты и, следовательно, приводимые в справочниках таблицы и графики имели большую общность, осуществляется нормировка частотной оси и ее трансформация таким образом, чтобы свести характеристики ФНЧ, ФВЧ, ППФ, ПЗФ к характеристикам эквивалентного ФНЧ-прототипа.
Амплитудно-частотная характеристика ФНЧ-прототипа определена на нормированной оси частот, причем граничная частота полосы пропускания 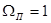 , а граничная частота полосы задержания
, а граничная частота полосы задержания 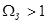 . В качестве нормирующей частоты для ФНЧ и ФВЧ выбирается граничная частота полосы пропускания
. В качестве нормирующей частоты для ФНЧ и ФВЧ выбирается граничная частота полосы пропускания 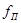 , а для ППФ и ПЗФ – центральная частота полоса пропускания (задержания)
, а для ППФ и ПЗФ – центральная частота полоса пропускания (задержания) 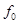 . Формулы для вычисления нормированных частот синтезируемого фильтра и его ФНЧ-прототипа приведены в таблице 2.1.[1] Обозначение частоты с тильдой (
. Формулы для вычисления нормированных частот синтезируемого фильтра и его ФНЧ-прототипа приведены в таблице 2.1.[1] Обозначение частоты с тильдой ( 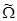 ) относится к проектируемому фильтру, а без тильды (
) относится к проектируемому фильтру, а без тильды ( 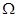 ) – к ФНЧ-прототипу. При синтезе ППФ и ПЗФ определяется коэффициент геометрической асимметрии
) – к ФНЧ-прототипу. При синтезе ППФ и ПЗФ определяется коэффициент геометрической асимметрии 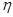 , в зависимости от значения, которого по-разному вычисляют нормированные частоты. Важно проконтролировать, чтобы всегда выполнялись условия:
, в зависимости от значения, которого по-разному вычисляют нормированные частоты. Важно проконтролировать, чтобы всегда выполнялись условия: 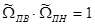 и
и 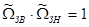 . В противном случае невозможно правильное преобразование ППФ и ПЗФ из ФНЧ-прототипа.
. В противном случае невозможно правильное преобразование ППФ и ПЗФ из ФНЧ-прототипа.
Итак, требования к АЧХ ФНЧ-прототипа найдены. Они выражаются тремя параметрами: 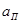 ,
, 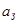 и
и 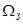 .
.
Передаточная функция и АЧХ.
Располагая координатами нулей и полюсов синтезируемого фильтра, можно записать передаточную функцию:
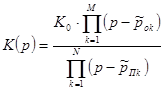 , (2.1)
, (2.1)
где 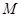 - количество нулей,
- количество нулей, 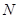 - количество полюсов синтезируемого фильтра,
- количество полюсов синтезируемого фильтра, 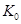 - нормировочный коэффициент. Диаграмма нулей и полюсов определяет передаточную функцию с точностью до постоянного множителя, но на форму АЧХ это не оказывает влияния. АЧХ удобно представлять в нормированном виде. С этой целью коэффициент
- нормировочный коэффициент. Диаграмма нулей и полюсов определяет передаточную функцию с точностью до постоянного множителя, но на форму АЧХ это не оказывает влияния. АЧХ удобно представлять в нормированном виде. С этой целью коэффициент 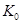 выбирается таким, чтобы
выбирается таким, чтобы 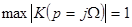 . Значения коэффициента
. Значения коэффициента 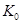 для различных видов приведены в таблице 2.5.[3] В ней
для различных видов приведены в таблице 2.5.[3] В ней 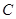 - это коэффициент, взятый из последней колонки таблицы справочника,
- это коэффициент, взятый из последней колонки таблицы справочника, 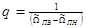 - параметр преобразования для ППФ и ПЗФ,
- параметр преобразования для ППФ и ПЗФ, 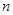 - порядок ФНЧ-прототипа. Итак, для фильтра Чебышева ППФ значение коэффициента
- порядок ФНЧ-прототипа. Итак, для фильтра Чебышева ППФ значение коэффициента 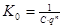 .
.
Расчет.
Заданные технические требования представлены как Таблица 1.
Таблица 1
| Тип фильтра | 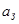 , [дБ] , [дБ]
|  , [дБ] , [дБ]
| 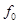 , [кГц] , [кГц]
| 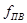 , [кГц] , [кГц]
| 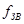 , [кГц] , [кГц]
| 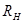 , [Ом] , [Ом]
|
| Чебышев | 35 | 1.25 | 100 | 120 | 150 | 50 |
Отталкиваясь от таблицы 2.1[4], рассчитаем нормированные частоты синтезируемого фильтра:
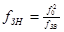 ,
, 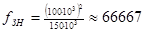 ;
;
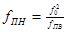 ,
, 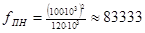 ;
;
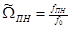 ,
, 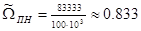 ;
;
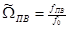 ,
, 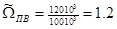 ;
;
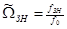 ,
, 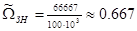 ;
;
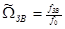 ,
, 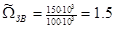 ;
;
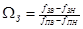 ,
, 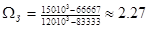 ;
;
Коэффициент геометрической асимметрии 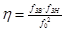 равен 1. А центральна циклическая частота полосы пропускания
равен 1. А центральна циклическая частота полосы пропускания 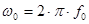 .
.
После проведенного анализа данных с помощью справочника, были определены параметры: тип, порядок фильтра, полюсы и нули ФНЧ-прототипа, а также нормированные значения элементов цепи.
Таблица 2
| Порядок фильтра | 
| 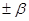
| 
| 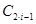
| 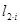
|
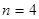
| 0.447 | 0.327 | 1 | 1.614 | 1.55 |
| 0.151 | 0.972 | 2 | 1.610 | 0.836 |
Отталкиваясь от таблицы 2.4[5], рассчитаем полюсы и нули необходимого нам ППФ.
| Нули | Полюсы |
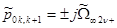 , ,
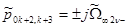 ,
где ,
где 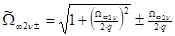
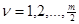 , ,
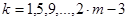 , ,
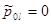 , ,
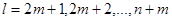 . .
| 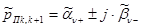 , , 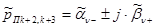 ,
где ,
где 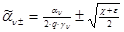 , , 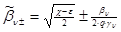 , ,
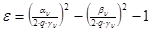 , , 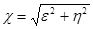 , ,
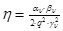 , , 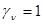 , , 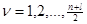 , ,
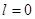 , , 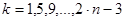 , ,
|
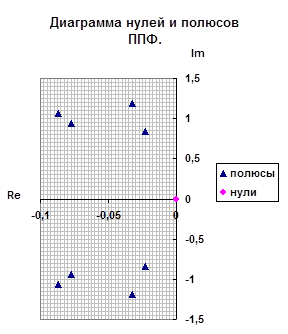
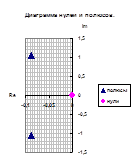
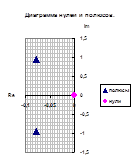
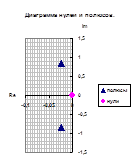
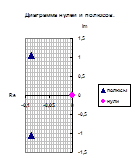
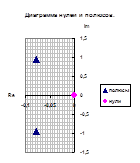
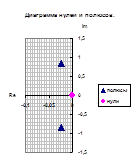
Полученные значения запишем как Таблица 3 и отобразим на диаграмме нулей и полюсов.
Таблица 3
| Полюсы и нули. | 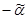
| 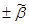
|
| полюсы | 0,077029470702035 | 0,93850000456136 |
| 0,086870529297965 | 1,05840000456136 | |
| 0,022824923789752 | 0,83718784570175 | |
| 0,032541742876915 | 1,19358784570175 | |
| нули | 0 | 0 |
| 0 | 0 |
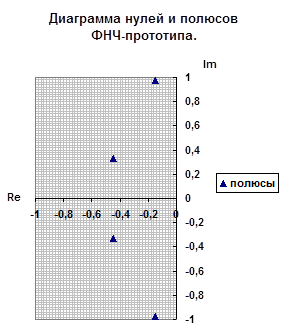
| 
|
Теперь с помощью формулы 2.1, где 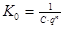 ,
, 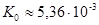 , а
, а 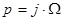 , по полученным полюсам и нулям построим АЧХ ППФ, причем АЧХ равно
, по полученным полюсам и нулям построим АЧХ ППФ, причем АЧХ равно 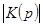 .
.

Теория.
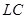 - фильтр с лестничной структурой представляет собой пассивную линейную цепь, построенную путем соединения индуктивностей и емкостей. Такая схема имеет многочисленные внутренние связи. Метод расчета лестничных структур предполагает переход к операторной схеме замещения цепи. Запись ее передаточной функции и сравнение выраженных через элементы схемы коэффициентов полиномов в числителе и знаменателе передаточной функции с коэффициентами полиномов передаточной функции, полученной на этапе аппроксимации. Решение сформированной системы уравнений позволяет определить значения элементов схемы. Такие расчеты выполнены на ЭВМ, а их результаты занесены в справочник.
- фильтр с лестничной структурой представляет собой пассивную линейную цепь, построенную путем соединения индуктивностей и емкостей. Такая схема имеет многочисленные внутренние связи. Метод расчета лестничных структур предполагает переход к операторной схеме замещения цепи. Запись ее передаточной функции и сравнение выраженных через элементы схемы коэффициентов полиномов в числителе и знаменателе передаточной функции с коэффициентами полиномов передаточной функции, полученной на этапе аппроксимации. Решение сформированной системы уравнений позволяет определить значения элементов схемы. Такие расчеты выполнены на ЭВМ, а их результаты занесены в справочник.
При реализации 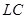 - структуры следует совершить следующие шаги:
- структуры следует совершить следующие шаги:
1. Выписать из таблицы справочника нормированные значения элементов схемы ФНЧ-прототипа;
2. Вычислить, используя выписанные значения, величины элементов ППФ;
3. Денормировать значения элементов;
4. Составить принципиальную схему фильтра.
В схемах могут использоваться идеальные и реальные источники тока или напряжения, применяемые для ввода входного сигнала. Все элементы нормированы относительно сопротивления нагрузки и граничной частоты полосы пропускания. Порядок фильтра определяется числом последовательных ветвей (звеньев), которые для удобства пронумерованы.
При проектировании ФВЧ, ППФ, ПЗФ необходимо пересчитать значения элементов схемы ФНЧ-прототипа в значения элементов синтезируемого фильтра и нарисовать его схему. С этой целью нужно обратится к таблице 3.1.[6]
Чтобы получить реальные величины индуктивностей и емкостей, следует провести операцию денормирования значений элементов. Отношение сопротивления нагрузки к реальному сопротивлению индуктивности или емкости сохраняется в нормированном и денормированном виде, а именно:
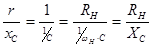 ,
, 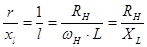 .
.
Отсюда находим формулы для денормирования емкостей и индуктивностей:
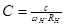 ,
, 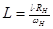 ,
,
где 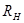 - сопротивление нагрузки (приводится в задании),
- сопротивление нагрузки (приводится в задании), 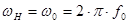 .
.
В результате расчета элементов может оказаться, что номиналы индуктивностей и емкостей одиночных параллельных контуров на несколько порядков отличаются от значений соответствующих элементов, стоящих в других звеньях. Это неудобно, поскольку повышает чувствительность характеристик фильтра к изменениям величин элементов. Чтобы избежать ухудшения характеристик, следует использовать автотрансформаторное включение контура, где 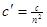 ,
, 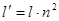 ,
, 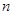 - коэффициент трансформации.
- коэффициент трансформации.
Расчет.
Итак, используя вышесказанное, получим лестничную 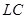 - структуру:
- структуру:
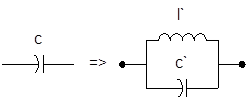
| 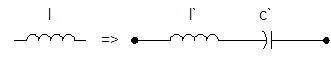
|
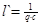 , , 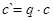
| 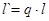 , , 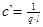
|
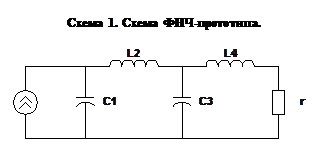
Схема 2 . Принципиальная схема синтезируемого ППФ.
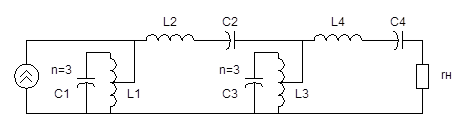
Пересчитаем значения элементов (  ):
):
| Номер, i | 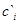
| 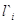
|
| 1 | 4.401818 | 0.227179 |
| 2 | 0.236559 | 4.227272 |
| 3 | 4.390909 | 0.227743 |
| 4 | 0.438596 | 2.280000 |
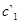 и
и 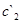 ,
, 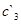 и
и 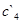 ,
, 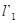 и
и 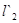 ,
, 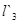 и
и 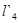 отличаются на порядок. Чтобы устранить такие резкие различия, Положим коэффициент трансформации
отличаются на порядок. Чтобы устранить такие резкие различия, Положим коэффициент трансформации 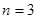 . В этом случае (смотри таблицу 3.2[7]) получим новые значения:
. В этом случае (смотри таблицу 3.2[7]) получим новые значения:
| Номер, i | 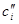
| 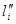
|
| 1 | 0.489090 | 2.044611 |
| 2 | 0.236559 | 4.227272 |
| 3 | 0.487878 | 2.049687 |
| 4 | 0.438596 | 2.280000 |
Проведем денормирование элементов, полученной электрической цепи:
| Номер, i | 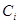 , [нФ] , [нФ]
| 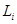 , [мГн] , [мГн]
|
| 1 | 15.57 | 0.163 |
| 2 | 7.53 | 0.336 |
| 3 | 15.53 | 0.163 |
| 4 | 13.96 | 0.181 |
Каскадное соединение 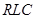 - звеньев.
- звеньев.
Теория.
Существует возможность реализовать фильтр путем каскадного соединения 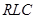 - звеньев первого и второго порядка. Каждое из звеньев рассчитывается независимо от других. Для сведения к минимуму (в первом приближении – исключения вообще) взаимовлияния звеньев между ними ставят буферный каскад (БК). Такой каскад должен обладать высоким входным сопротивлением, значительно превышающим выходное сопротивление
- звеньев первого и второго порядка. Каждое из звеньев рассчитывается независимо от других. Для сведения к минимуму (в первом приближении – исключения вообще) взаимовлияния звеньев между ними ставят буферный каскад (БК). Такой каскад должен обладать высоким входным сопротивлением, значительно превышающим выходное сопротивление 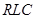 - звеньев, и малым выходным сопротивлением, позволяющим считать БК почти идеальным источником напряжения для последующего
- звеньев, и малым выходным сопротивлением, позволяющим считать БК почти идеальным источником напряжения для последующего 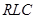 - звена. В других типах БК выходная цепь работает как источник тока. В качестве БК используется эмиттерный или истоковый повторитель, повторитель на операционном усилителе (ОУ), усилитель на транзисторе или ОУ.
- звена. В других типах БК выходная цепь работает как источник тока. В качестве БК используется эмиттерный или истоковый повторитель, повторитель на операционном усилителе (ОУ), усилитель на транзисторе или ОУ.
Синтез каскадной структуры 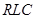 - фильтра нужно начать с представления передаточной функции, полученной на этапе аппроксимации, в виде произведения дробей-сомножителей.
- фильтра нужно начать с представления передаточной функции, полученной на этапе аппроксимации, в виде произведения дробей-сомножителей.
Важно правильно сгруппировать нули и полюсы, чтобы минимизировать чувствительность схемы к изменениям параметров элементов. Наиболее простое правило состоит в том, что нужно объединять нули с ближайшими к ним полюсами.
Каждый фрагмент передаточной функции реализуется своей схемой. Метод расчета состоит в сопоставлении коэффициентов передаточной функции, полученной на этапе аппроксимации, с коэффициентами, выраженными через элементы схемы. В таблице 3.3[8] приведены семь вариантов схем 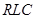 - звеньев первого и второго порядка, входной сигнал, в которые вводится источником напряжения, показаны диаграммы нулей и полюсов и их связь с передаточной функцией. Рядом со схемами помещены денормированные передаточные функции
- звеньев первого и второго порядка, входной сигнал, в которые вводится источником напряжения, показаны диаграммы нулей и полюсов и их связь с передаточной функцией. Рядом со схемами помещены денормированные передаточные функции 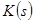 , где
, где 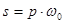 для ППФ.
для ППФ.
В таблице 3.3 дается также порядок расчета каждого звена. При расчете любой из схем есть одна степень свободы. Предлагается задавать значение сопротивления, хотя вполне можно было бы задаваться величиной емкости или индуктивности, а остальные элементы рассчитать на основе имеющихся связей. Активные сопротивления, стоящие ближе к входу в последовательной ветви, должны учитывать сопротивление источника напряжения, подключенного к входу схемы. В качестве этого сопротивления может выступать выходное сопротивление предыдущего буферного каскада. Однако, если 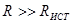 , то сопротивлением источника
, то сопротивлением источника 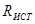 можно пренебречь. В таблице 3.4[9] представлены аналогичные сведения о схеме, входной сигнал, в которые вводится источником тока. В этом случае передаточная функция определяется как отношение изображения по Лапласу выходного напряжения к изображению входного тока и имеет смысл сопротивления прямой передачи.
можно пренебречь. В таблице 3.4[9] представлены аналогичные сведения о схеме, входной сигнал, в которые вводится источником тока. В этом случае передаточная функция определяется как отношение изображения по Лапласу выходного напряжения к изображению входного тока и имеет смысл сопротивления прямой передачи.
Выбор типов звеньев, включаемых в синтезируемую схему, определяется на основе анализа диаграммы нулей и полюсов, а также вида передаточных функций первого и второго порядка, произведение которых дает реализуемую функцию. Следует обращать внимание на то, что источником напряжения или тока является БК для последующего 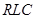 - звена.
- звена.
Расчет.
Итак, обратимся к таблице 3.4 и выберем нужный нам вариант схем:
| Схема и диаграмма нулей и полюсов. | Передаточная функция | Расчет |
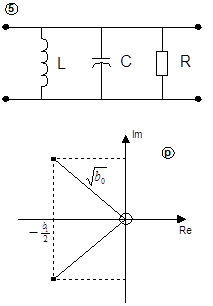
| 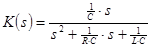
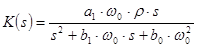
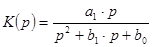 , , 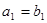
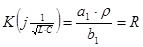
| 1. Выбор 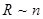 кОм или кОм или 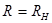 ,
2. ,
2. 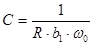 ,
3. ,
3. 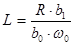 . .
|
Сгруппируем нули и полюсы, отталкиваясь от диаграммы нулей и полюсов ППФ:
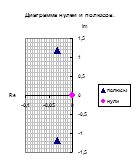
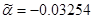 , , 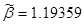
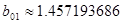
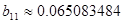
 [кОм] [кОм]
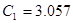 [нФ] [нФ]
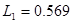 [мГн] [мГн]
| 
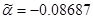 , , 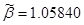
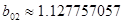
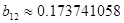
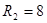 [кОм] [кОм]
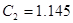 [нФ] [нФ]
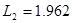 [мГн] [мГн]
| 
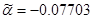 , , 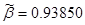
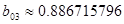
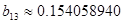
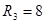 [кОм] [кОм]
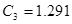 [нФ] [нФ]
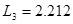 [мГн] [мГн]
| 
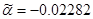 , , 
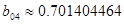
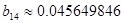
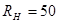 [Ом] [Ом]
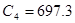 [нФ] [нФ]
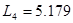 [мкГн] [мкГн]
|
Запишем передаточную функцию, исходя из диаграмм нулей и полюсов.
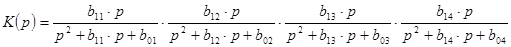
И нарисуем принципиальную схему синтезируемого ППФ, см. Схема 3.
Схема 3. Каскадные соединения RLC-звеньев.

Теория.
При использовании катушек индуктивности на низких частотах возникает множество неудобств, поэтому разработаны схемы, лишенные этих элементов. Рассмотрим схему фильтра, получаемую из лестничной 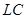 -структуры заменой катушек индуктивности на гираторы, в качестве нагрузки которых используется емкостное сопротивление. Гиратором называется устройство, преобразующее импеданс. В частности, гиратор, нагруженный на емкость, ведет себя на входных зажимах как индуктивность. Схема гиратора представлена как Схема 4.
-структуры заменой катушек индуктивности на гираторы, в качестве нагрузки которых используется емкостное сопротивление. Гиратором называется устройство, преобразующее импеданс. В частности, гиратор, нагруженный на емкость, ведет себя на входных зажимах как индуктивность. Схема гиратора представлена как Схема 4.
Схема 4. Гиратор.
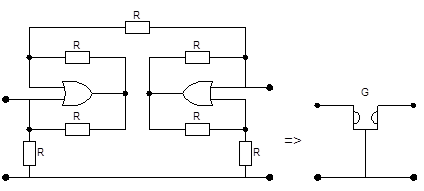
Гирпторные схемы являются разновидностью активных 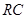 -фильтров (
-фильтров ( 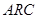 -фильтров) и часто носят название активных лестничных фильтров (АЛФ). Основное соотношение гиратора:
-фильтров) и часто носят название активных лестничных фильтров (АЛФ). Основное соотношение гиратора:
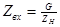 , (3.2)
, (3.2)
где 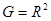 - коэффициент гирации;
- коэффициент гирации; 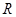 - сопротивление, используемое в схеме гиратора.
- сопротивление, используемое в схеме гиратора.
В частности, если 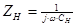 , то получим из (3.2)
, то получим из (3.2) 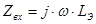 , где
, где 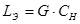 .
.
На рисунке 3.6[10] представлены основные преобразования индуктивностей, включенных в последовательные и параллельные ветви, 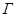 - и
- и 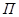 -образных звеньев индуктивностей
-образных звеньев индуктивностей  -структур. Такие преобразования позволяют составить схему АЛФ с наименьшим числом гираторов.
-структур. Такие преобразования позволяют составить схему АЛФ с наименьшим числом гираторов.
Порядок расчета АЛФ следующий:
1. составить схему АЛФ на основе схемы 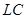 -фильтра, рассчитанной ранее;
-фильтра, рассчитанной ранее;
2. найти емкости, полученные преобразованием соответствующих индуктивностей, по формуле 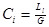 . Коэффициент гирации подбирается таким, чтобы получающиеся значения емкостей были одного порядка со значениями емкостных элементов, уже использованными в лестничной
. Коэффициент гирации подбирается таким, чтобы получающиеся значения емкостей были одного порядка со значениями емкостных элементов, уже использованными в лестничной  -структуре.
-структуре.
Расчет.
Используя одну из схем замещения на рисунке 3.6.
Схема 5. Схема замещения.
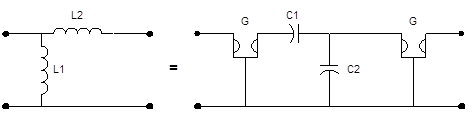
Составим схему АЛФ на основе 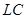 -фильтра.
-фильтра.
Схема 6. Гираторная реализация безиндуктивного фильтра.
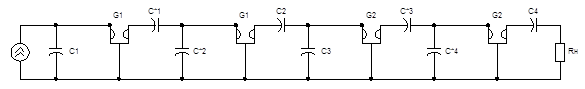
Уменьшим заданные частоты на порядок, то есть 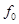 = 1000 [Гц],
= 1000 [Гц], 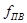 = 1200 [Гц],
= 1200 [Гц], 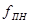 = 833 [Гц],
= 833 [Гц], 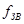 = 1500 [Гц],
= 1500 [Гц], 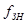 = 667 [Гц]. И пересчитаем значения элементов для новых частот:
= 667 [Гц]. И пересчитаем значения элементов для новых частот:
| Номер, i | 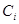 , [мкФ] , [мкФ]
| 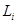 , [мГн] , [мГн]
|
| 1 | 14.01 | 1.808 |
| 2 | 0.753 | 33.64 |
| 3 | 13.98 | 1.812 |
| 4 | 1.396 | 18.14 |
Теперь найдем емкости, полученные преобразованием соответствующих индуктивностей, по формуле 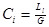 . Пусть
. Пусть 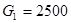 и
и 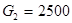 , тогда элементная база схемы будет выглядеть следующим образом:
, тогда элементная база схемы будет выглядеть следующим образом: 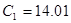 [мкФ],
[мкФ], 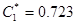 [мкФ],
[мкФ], 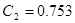 [мкФ],
[мкФ],  [мкФ],
[мкФ], 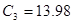 [мкФ],
[мкФ], 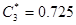 [мкФ],
[мкФ], 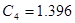 [мкФ],
[мкФ], 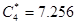 [мкФ].
[мкФ].
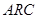 -фильтр с каскадной структурой.
-фильтр с каскадной структурой.
Теория.
Подход к реализации 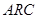 -фильтра, собираемого из звеньев первого и второго порядка, аналогичен тому способу построения фильтра, который был описан при реализации
-фильтра, собираемого из звеньев первого и второго порядка, аналогичен тому способу построения фильтра, который был описан при реализации 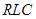 -звеньев.
-звеньев. 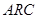 -звенья строятся без использования индуктивностей. Звено представляет собой соединение одного, двух или трех операционных усилителей (ОУ) с резистивно-емкостной цепью. Применение обратных связей позволяет реализовывать все возможные конфигурации действительных и комплексных нулей и полюсов. Перед тем как приступить к расчету звеньев, необходимо разбить передаточную функцию, полученную на этапе аппроксимации, на сомножители. Тем самым нули и полюсы будут поделены на группы, поддающиеся реализации с помощью звеньев первого и второго порядка. Примеры группирования нулей и полюсов даны на рисунке 3.4.[11] Конкретные схемы, диаграммы полюсов и нулей, соответствующие им, а также расчетные соотношения можно отыскать в таблице 3.5.[12]
-звенья строятся без использования индуктивностей. Звено представляет собой соединение одного, двух или трех операционных усилителей (ОУ) с резистивно-емкостной цепью. Применение обратных связей позволяет реализовывать все возможные конфигурации действительных и комплексных нулей и полюсов. Перед тем как приступить к расчету звеньев, необходимо разбить передаточную функцию, полученную на этапе аппроксимации, на сомножители. Тем самым нули и полюсы будут поделены на группы, поддающиеся реализации с помощью звеньев первого и второго порядка. Примеры группирования нулей и полюсов даны на рисунке 3.4.[11] Конкретные схемы, диаграммы полюсов и нулей, соответствующие им, а также расчетные соотношения можно отыскать в таблице 3.5.[12]
При расчете следует иметь в виду:
1. Выбор той или иной схемы, включаемой в каскадное соединение, определяется диаграммой нулей и полюсов синтезируемого фильтра. Возможно, также ориентироваться на вид передаточной функции звена.
2. Звенья на одном операционном усилителе предназначены для реализации полюсов с невысокими добротностями. Добротность полюса вычисляется по формуле 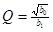 . Если
. Если 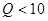 , то можно использовать простые схемы типа 3…7. При
, то можно использовать простые схемы типа 3…7. При  следует применять более сложные схемы типа 8…12.
следует применять более сложные схемы типа 8…12.
3. 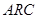 -схемы сочетать фильтрацию с усилением. Заданный коэффициент усиления следует распределить по каскадам так, чтобы
-схемы сочетать фильтрацию с усилением. Заданный коэффициент усиления следует распределить по каскадам так, чтобы 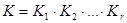 , где
, где 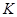 - общий коэффициент усиления,
- общий коэффициент усиления, 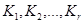 - коэффициент усиления каскадов.
- коэффициент усиления каскадов.
4. После расчета элементов звеньев нужно выбрать номинальные значения, наиболее близкие к вычисленным, и, кроме того, подобрать конкретный тип микросхемы ОУ.
Предлагаемый расчет 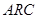 -звеньев упрощенный. С более сложной методикой, включающей в себя оценку нестабильности характеристик фильтра, расчет нелинейных искажений и допустимого динамического диапазона, можно ознакомится в дополнительной литературе.
-звеньев упрощенный. С более сложной методикой, включающей в себя оценку нестабильности характеристик фильтра, расчет нелинейных искажений и допустимого динамического диапазона, можно ознакомится в дополнительной литературе.
Порядок включения каскадов тоже важен. Нужно, чтобы перед звеном, имеющим всплеск АЧХ на некоторой частоте, стояло звено, обладающее на этой частоте небольшим значение АЧХ. Это достигается включением каскадов друг за другом в порядке увеличения добротности реализуемых полюсов.
Расчет.
Итак, обратимся к таблице 3.5 и выберем нужный нам вариант схем:
| Схема и диаграмма нулей и полюсов. | Передаточная функция | Расчет |

| 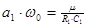
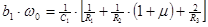
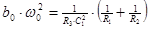
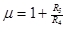
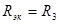
| 1.  2.
2. 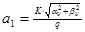 , где , где 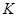 - коэффициент усиления звена, - коэффициент усиления звена, 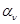 и и 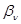 - координаты полюса ФНЧ-прототипа, - координаты полюса ФНЧ-прототипа, 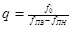 3. Выбор
3. Выбор 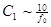 [мкФ]
4. [мкФ]
4. 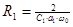 5.
5. 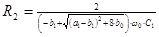 6.
6. 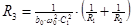 7.
7. 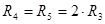
|
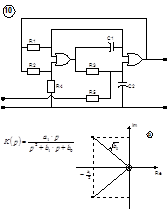
| 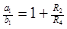
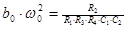
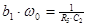
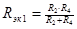
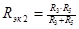
| 1. 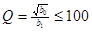 2.
2. 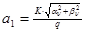 , где , где 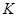 - коэффициент усиления звена, - коэффициент усиления звена, 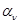 и и 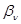 - координаты полюса ФНЧ-прототипа, - координаты полюса ФНЧ-прототипа, 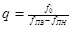 3. Выбор
3. Выбор 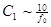 [мкФ]
4. [мкФ]
4. 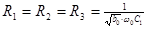 5.
5. 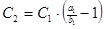 6.
6. 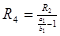 7.
7. 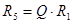
|
Уменьшим заданные частоты на порядок, то есть 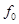 = 1000 [Гц],
= 1000 [Гц], 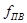 = 1200 [Гц],
= 1200 [Гц], 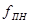 = 833 [Гц],
= 833 [Гц], 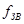 = 1500 [Гц],
= 1500 [Гц], 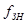 = 667 [Гц].
= 667 [Гц].
Сгруппируем нули и полюсы, отталкиваясь от диаграммы нулей и полюсов ППФ:
| Первый каскад | Второй каскад | Третий каскад | Четвертый каскад |
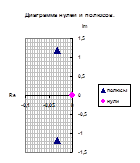
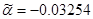 , , 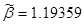
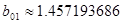

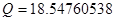
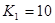
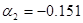 , , 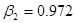
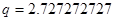
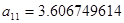
| 
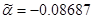 , , 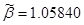
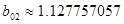
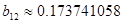
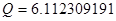
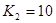
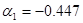 , , 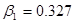
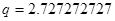
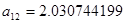
| 
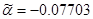 , , 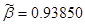
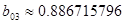
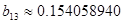
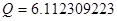

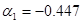 , , 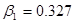
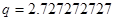
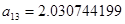
| 
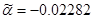 , , 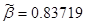
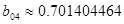
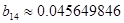
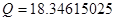
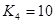
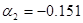 , , 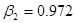
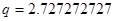
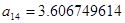
|
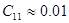 [мкФ] [мкФ]
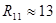 [кОм] [кОм]
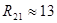 [кОм] [кОм]
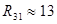 [кОм] [кОм]
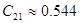 [мкФ] [мкФ]
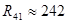 [Ом] [Ом]
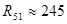 [кОм] [кОм]
| 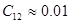 [мкФ] [мкФ]
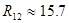 [кОм] [кОм]
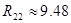 [кОм] [кОм]
 [кОм] [кОм]
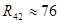 [кОм] [кОм]

|  [мкФ] [мкФ]
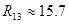 [кОм] [кОм]
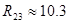 [кОм] [кОм]
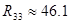 [кОм] [кОм]
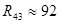 [кОм] [кОм]
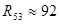 [кОм] [кОм]
| 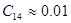 [мкФ] [мкФ]
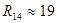 [кОм] [кОм]
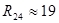 [кОм] [кОм]
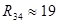 [кОм] [кОм]
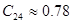 [мкФ] [мкФ]
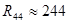 [Ом] [Ом]
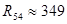 [кОм] [кОм]
|
Запишем передаточную функцию, исходя из диаграмм нулей и полюсов.
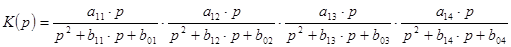
А теперь найдем принципиальную схему для реализации 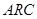 -фильтра.
-фильтра.
Схема 7. Схема ARC-реализации.

Литература.
1. В. В. Голованов, А. О. Яковлев, "Проектирование аналоговых и цифровых фильтров", издательство МАИ, 1993.
2. Тронин Ю. В., Гурский О. В., "Синтез фильтров", издательство МАИ, 1990.
3. Конспект лекций.
[1] В. В. Голованов, А. О. Яковлев, "Проектирование аналоговых и цифровых фильтров", издательство МАИ, 1993.
[2] В. В. Голованов, А. О. Яковлев, "Проектирование аналоговых и цифровых фильтров", издательство МАИ, 1993.
[3] В. В. Голованов, А. О. Яковлев, "Проектирование аналоговых и цифровых фильтров", издательство МАИ, 1993.
[4] В. В. Голованов, А. О. Яковлев, "Проектирование аналоговых и цифровых фильтров", издательство МАИ, 1993.
[5] В. В. Голованов, А. О. Яковлев, "Проектирование аналоговых и цифровых фильтров", издательство МАИ, 1993.
[6] В. В. Голованов, А. О. Яковлев, "Проектирование аналоговых и цифровых фильтров", издательство МАИ, 1993.
[7] В. В. Голованов, А. О. Яковлев, "Проектирование аналоговых и цифровых фильтров", издательство МАИ, 1993.
[8] В. В. Голованов, А. О. Яковлев, "Проектирование аналоговых и цифровых фильтров", издательство МАИ, 1993.
[9] В. В. Голованов, А. О. Яковлев, "Проектирование аналоговых и цифровых фильтров", издательство МАИ, 1993.
[10] В. В. Голованов, А. О. Яковлев, "Проектирование аналоговых и цифровых фильтров", издательство МАИ, 1993.
[11] В. В. Голованов, А. О. Яковлев, "Проектирование аналоговых и цифровых фильтров", издательство МАИ, 1993.
[12] В. В. Голованов, А. О. Яковлев, "Проектирование аналоговых и цифровых фильтров", издательство МАИ, 1993.
Курсовая работа
на тему
| Синтез частотно-избирательного фильтра. |
| Выполнил: | студент группы ##-### Гуренков Дмитрий |
| Проверил: | преподаватель Ручьев М. К. |
Москва 2011 г.
Содержание
Задание................................................................................................................................................................................. 3
Исходные данные...................................................................................................................................................... 3
Аппроксимация частотной характеристики фильтра............................................................ 4
Последовательность шагов....................................................................................................................................... 4
Тип фильтра........................................................................................................................................................................ 4
Требования к ФНЧ-прототипу.................................................................................................................................... 4
Порядок, нули и полюсы ФНЧ-прототипа............................................................................................................ 5
Нули и полюсы синтезируемого фильтра........................................................................................................... 5
Передаточная функция и АЧХ................................................................................................................................... 6
Расчет................................................................................................................................................................................... 6
Реализация аналогового фильтра............................................................................................................. 9
Лестничная 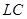 - структура....................................................................................................................................... 9
- структура....................................................................................................................................... 9
Теория................................................................................................................................................................................ 9
Расчет............................................................................................................................................................................. 10
Каскадное соединение 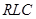 - звеньев............................................................................................................. 11
- звеньев............................................................................................................. 11
Теория............................................................................................................................................................................. 11
Расчет............................................................................................................................................................................. 12
Гираторная реализация безиндуктивного фильтра...................................................................................... 13
Теория............................................................................................................................................................................. 13
Расчет............................................................................................................................................................................. 14
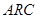 -фильтр с каскадной структурой............................................................................................................... 14
-фильтр с каскадной структурой............................................................................................................... 14
Теория............................................................................................................................................................................. 14
Расчет............................................................................................................................................................................. 15
Сравнительная характеристика различных реализаций синтезируемого фильтра. 17
Литература..................................................................................................................................................................... 18
Задание
1. Представить данные на синтез частотно-избирательного фильтра в графической форме с использованием нормированной частоты 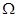 .
.
2. Определить технические требования к нормированному ФНЧ прототипу: тип и порядок фильтра.
3. Найти координаты нулей и полюсов нормированной передаточной функции ФНЧ прототипа.
4. Найти лестничную структуру ФНЧ прототипа с нормированными элементами.
5. Определить координаты нулей и полюсов передаточной функции синтезируемого частотно-избирательного фильтра. Построить график АЧХ с использованием денормированной частоты 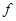 .
.
6. Определить лестничную структуру синтезируемого фильтра с нормированными элементами и провести денормирование элементов.
7. Выбрать возможные варианты RLC-звеньев первого и второго порядков, предназначенных для каскадной реализации фильтра, рассчитать величины элементов и составить полную схему фильтра.
8. Уменьшив частотные параметры на два порядка:
8.a. Составить схему и провести расчет элементов для гираторной реализации фильтра.
8.b. Выбрать возможные варианты ARC-звеньев первого и второго порядков, предназначенные для безиндукционной каскадной реализации фильтра, рассчитать величины элементов и составить полную схему фильтра.
9. Сделать вывод, дав сравнительную характеристику различным вариантам реализации синтезируемого фильтра.
Исходные данные
Задача синтеза фильтра состоит в разработке электрической схемы устройства, обладающего требуемыми частотными и временными характеристиками. Курсовая работа предполагает проектирование фильтра на основе требования к форме его характеристики затухания. При синтезе полосно-пропускающего фильтра вводится требование к верхним и нижним граничным частотам полосы пропускания ( 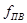 ,
, 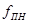 ,
, 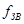 ,
, 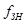 ).
).
 Амплитудно-частотная характеристика (АЧХ) фильтра
Амплитудно-частотная характеристика (АЧХ) фильтра 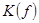 и характеристика затухания
и характеристика затухания 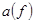 связаны друг с другом выражением
связаны друг с другом выражением
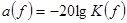 ,
,
поэтому при рассмотрении требований к АЧХ необходимо вместо допусков 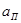 и
и 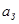 ввести параметры:
ввести параметры: 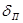 - допустимую неравномерность в полосе пропускания и
- допустимую неравномерность в полосе пропускания и 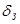 - максимально допустимую передачу в полосе задержания, причем
- максимально допустимую передачу в полосе задержания, причем
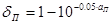 ,
, 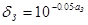 .
.
Типичная АЧХ полосно-пропускного фильтра Чебышева приведена на рисунке.
Процедура проектирования частотно-избирательного фильтра включает в себя два основных этапа:
1. Этап проектирования, в ходе которого подбирается передаточная функция, удовлетворяющая заданным требованиям (АЧХ, выделенная из аппроксимирующей передаточной функции, не должна выходить за пределы заданного коридора допусков);
2. Этап реализации, суть которого – в выборе принципа реализации передаточной функции, разработке и расчете конкретной схемы фильтра, обладающего найденной передаточной функцией.
Порядок выполнения первого этапа достаточно хорошо разработан, поставленная задача решается с использованием какого-либо из многочисленных справочников по расчету фильтров. Решение второй задачи в рамках второго этапа многовариантно. Это связано с тем, что известно довольно много принципов и схем, позволяющих реализовать найденную передаточную функцию.
Аппроксимация частотной характеристики фильтра
Последовательность шагов
На этапе аппроксимации необходимо проделать следующее:
1. Выбрать тип фильтра.
2. Пересчитать исходные данные в требования к фильтру – прототипу нижних частот (ФНЧ-прототипу).
3. Определить минимальный порядок ФНЧ-прототипа, нули и полюсы его передаточной функции (с помощью справочника).
4. Пересчитать нули и полюса ФНЧ-прототипа в нули и полюсы синтезируемого фильтра.
5. Записать передаточную функцию фильтра, найти и построить АЧХ или характеристику затухания.
Тип фильтра
Существует ряд типов фильтров, различающихся по характеру их передаточных функций. Например, фильтр Баттерворта, фильтр Чебышева, эллиптический (Золоторева - Каура) фильтр. Каждый из указанных типов в определенном смысле оптимален. Главная же особенность состоит в том, что заданную избирательность фильтр Чебышева обеспечивает при меньшем порядке, чем фильтр Баттерворта, а эллиптический фильтр в этом смысле лучше чебышевского.
Требования к ФНЧ-прототипу
Для того чтобы не было привязки начального этапа расчета к конкретным значениям частоты и, следовательно, приводимые в справочниках таблицы и графики имели большую общность, осуществляется нормировка частотной оси и ее трансформация таким образом, чтобы свести характеристики ФНЧ, ФВЧ, ППФ, ПЗФ к характеристикам эквивалентного ФНЧ-прототипа.
Амплитудно-частотная характеристика ФНЧ-прототипа определена на нормированной оси частот, причем граничная частота полосы пропускания 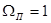 , а граничная частота полосы задержания
, а граничная частота полосы задержания 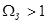 . В качестве нормирующей частоты для ФНЧ и ФВЧ выбирается граничная частота полосы пропускания
. В качестве нормирующей частоты для ФНЧ и ФВЧ выбирается граничная частота полосы пропускания 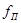 , а для ППФ и ПЗФ – центральная частота полоса пропускания (задержания)
, а для ППФ и ПЗФ – центральная частота полоса пропускания (задержания) 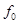 . Формулы для вычисления нормированных частот синтезируемого фильтра и его ФНЧ-прототипа приведены в таблице 2.1.[1] Обозначение частоты с тильдой (
. Формулы для вычисления нормированных частот синтезируемого фильтра и его ФНЧ-прототипа приведены в таблице 2.1.[1] Обозначение частоты с тильдой ( 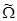 ) относится к проектируемому фильтру, а без тильды (
) относится к проектируемому фильтру, а без тильды ( 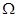 ) – к ФНЧ-прототипу. При синтезе ППФ и ПЗФ определяется коэффициент геометрической асимметрии
) – к ФНЧ-прототипу. При синтезе ППФ и ПЗФ определяется коэффициент геометрической асимметрии 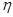 , в зависимости от значения, которого по-разному вычисляют нормированные частоты. Важно проконтролировать, чтобы всегда выполнялись условия:
, в зависимости от значения, которого по-разному вычисляют нормированные частоты. Важно проконтролировать, чтобы всегда выполнялись условия: 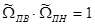 и
и 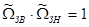 . В противном случае невозможно правильное преобразование ППФ и ПЗФ из ФНЧ-прототипа.
. В противном случае невозможно правильное преобразование ППФ и ПЗФ из ФНЧ-прототипа.
Итак, требования к АЧХ ФНЧ-прототипа найдены. Они выражаются тремя параметрами: 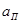 ,
, 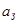 и
и 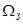 .
.
Дата: 2019-05-28, просмотров: 347.