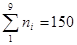При визначенні закону розподілення ресурсу дані випробувань групують за інтервалами напрацювання і підраховують кількість випадків попадання ресурсу в кожний інтервал. Далі, по вибраному теоретичному закону розподілення, визначають теоретичну ймовірність ресурсу для кожного інтервалу напрацювання і теоретичне число попадання ресурсу в кожний інтервал.
Відповідність експериментальних даних певному теоретичному закону розподілення можна перевірити за критерієм згоди Персона х2. В цьому випадку знаходять міру розходження х2 між дослідним (емпіричним) і теоретичним розподіленнями за формулою:
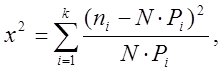(17)
де к – кількість інтервалів статистичного ряду;
n1 – кількість випадків попадання ресурсу в і-ий інтервал за даними випробувань;
Рі – теоретична ймовірність попадання ресурсу в і-ий інтервал;
N – число об’єктів, які приймали участь у випробуванні.
Додаток N·Рі в наведеній формулі (17) є теоретичним числом випадків попадання ресурсу в і-ий інтервал.
Після розрахунків значення х2, по таблиці 9 [1 ] з врахуванням кількості прийнятих інтервалів групування і виду прийнятого теоретичного закону розподілення визначають ймовірність дослідних і теоретичних даних.
Критичною ймовірністю збігу прийнято вважати ймовірність, яка більше 0,1. Якщо ж ймовірність збігу менше 0,1 , то отримане в результаті випробувань розподілення ресурсу не відповідає вибраному теоретичному закону. Ймовірність збігу, більша 0,1 свідчить про те, що вибраний теоретичний закон не суперечить дослідному розподіленню.
При такій перевірці слід врахувати, що навіть велика ймовірність збігу не гарантує того, що вибраний теоретичний закон найкращим чином описує отримане шляхом випробувань розподілення ресурсу. При цьому отримане дослідне розподілення ресурсу необхідно перевірити на відповідність декільком теоретичним законам розподілення. Після такої перевірки приймають той теоретичний закон, який відповідає максимальній ймовірності збігу.
1.7 Визначення ресурсу лемеша(приклад)
Приклад. В результаті випробувань 150 лемешів тракторного плуга (N=150) було встановлено, що ресурс лемеша розподілений в діапазоні 18...44 га при середньому значенні 
=25 га, середньоквадратичному відхиленні
σ=7,1 га і коефіцієнті варіації V=1,02. Визначити теоретичний закон розподілення ресурсу лемеша.
Рішення. Враховуючи, що значення коефіцієнта варіації ресурсу в даному випадку наближається до одиниці, необхідно застосувати гіпотезу про те, що розподілення ресурсу лемеша підлягає експоненціальному закону.
Тоді функція розподілення ресурсу лемеша, з врахуванням наявності зміщення (Т3=18 га), запишеться у вигляді:
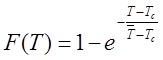(18)
Позначив Т-Тс=t і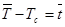 
, отримаємо
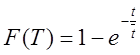(19)
Графік цієї функції в загальному вигляді показаний на рис.5.
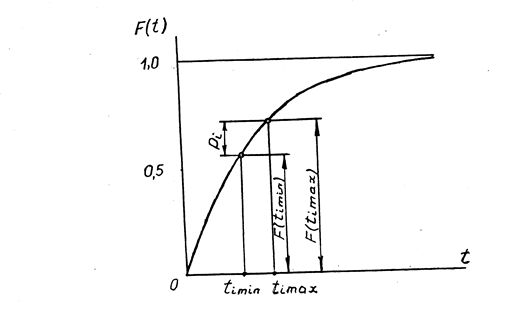
Рис.5. Інтегральний закон розподілення ресурсу при експоненціальному розподіленні: tmin, tmax – границі і-го інтервалу.
Як видно з графіка, теоретична ймовірність Рі попадання ресурсу в і-ий інтервал напрацювання визначається за формулою:
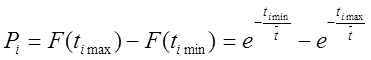(20)
Для перевірки висунутої гіпотези про розподілення ресурсу лемеша за законом Вейбулла весь діапазон варіації ресурсу розіб’ємо на 9 рівних інтервалів (табл.1.). Для кожного інтервалу підраховане число випадків попадання ресурсу в даний інтервал – п1 (із 150 дослідних даних). Множенням теоретичної ймовірності Р1 попадання ресурсу в кожен із інтервалів на загальне число N об’єктів, що випробуються, визначаємо необхідне число випадків попадання ресурсу в кожний виділений інтервал напрацювання, при умові, що ресурс лемеша розподілений строго за експоненціальним законом (визначене теоретичне число випадків – NP1).
Отримані дані дозволяють за формулою (17) визначити значення критерію Х2.
Всі розрахунки по визначенню Х2 зведені в табл.1. При заповнені колонки 7 і 8 зручно користуватися додатком 3. Визначаємо, що Х2=9,327.
При значенні Х2=9,327 і числі степенів вільності z=7, по таблиці додатку знаходимо, що ймовірність збігу дослідних і теоретичних даних перевищує 0,2 (0,3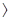 
Р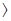 
0,2). Таким чином, прийнятий теоретичний закон експоненціального розподілення ресурсу лемешів не суперечить дослідним даним.
Аналогічні розрахунки критерію Х2 для перевірки гіпотези про те, що ресурс лемешів розподілений по нормальному закону, дають значно гірший результат (ймовірність збігу дослідних і теоретичних даних Р<(0,1).
При висуванні гіпотези про теоретичний закон розподілення ресурсу об’єкта, що випробовується, завжди виходять із величини отриманого за результатами дослідів коефіцієнта варіації ресурсу.
Таблиця.1.
Розрахунок критерію х2.
| № інтервалу | Границі інтервалу Тmin…Tmax | Границі інтервалу з врахуванням зміщення tmin…tmax | Частота в інтервалі n1 |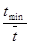 
| 
| 
| 
| 
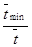
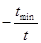
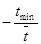
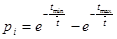
| NPi | ni-NPi | (ni-NPi)2 | |
| 1 2 3 4 5 6 7 8 9 | 18-21 21-24 24-27 27-30 30-33 33-36 36-39 39-42 42-45 | 0-3 3-6 6-9 9-12 12-15 15-18 18-21 21-24 24-27 | 57 30 21 15 9 5 4 5 4 | 0 0,43 0,86 1,29 1,71 2,14 2,57 3,00 3,43 | 0,43 0,86 1,29 1,71 2,14 2,57 3,00 3,43 3,86 | 1 0,650 0,424 0,297 0,181 0,118 0,076 0,050 0,032 | 0,650 0,424 0,297 0,181 0,118 0,076 0,050 0,032 0,021 | 0,350 0,226 0,127 0,116 0,063 0,042 0,026 0,018 0,011 | 52,5 33,9 19,0 17,3 9,4 6,3 3,9 2,7 1,7 | 4,5 -3,9 2,0 -2,3 -0,4 -1,3 -0,1 2,3 2,3 | 14,2 12,6 4,0 7,2 0,16 4,1 0,01 7,2 7,2 | 0,27 0,37 0,21 0,42 0,017 0,65 0,03 3,13 4,23 |
|
|
Х2=9,327 | |||||||||||
При цьому враховують, що для нормального закону розподілення V≤0,3; для закону Вейбулла V>0,3; при експоненціальному розподіленні V=1.
Напрацювання на відмову
Основним показником, який оцінює безвідмовність сільськогосподарської техніки є напрацювання на відмову – Тв.
Напрацювання на відмову – середнє напрацювання відновлюваного об’єкту між двома відмовами. Цей показник визначається за результатами спостережень за формулою:
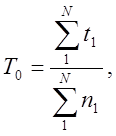(21)
де N – кількість об’єктів, які взяті на спостереження;
t1 – напрацювання і-го об’єкту за час спостереження;
n1 – кількість відмов і-го об’єкту за час спостереження.
Згідно ДСТУ 70/23.2.8 – 79 “Випробування сільськогосподарської техніки. Трактори і машини сільськогосподарські. Надійність. Збір і обробка інформації”, відмови складних виробів (тракторів, комбайнів і їх агрегатів) по трудомісткості усунення поділяються на 3 групи (найбільш складні – 3-ої групи). При оцінці безвідмовності цих об’єктів величина напрацювання на відмову повинна визначатися шляхом обробки результатів окремо по кожній групі складності.
Для тракторів і їх агрегатів, які пройшли капітальний ремонт, в якості їх безвідмовності прийнято рахувати кількість відмов кожної групи складності за кожні 1000 мото-годин роботи двигуна. В нормативах надійності капітально відремонтованих тракторів вказано допустима середня кількість відмов тієї чи іншої групи складності за кожну тисячу мото-годин роботи двигуна. Якість ремонту цих об’єктів з точки зору їх післяремонтної безвідмовності визначається встановленням фактичного середнього числа відмов кожної з трьох груп складності на тисячу мото-годин і порівнюємо їх з нормативними значеннями.
Для визначення фактичного середнього числа відмов кожної з трьох груп складності на тисячу мото-годин спочатку за результатами випробувань знаходять середнє кількість відмов даного виду mT у об’єкта за напрацювання Т, на протязі якого проводились спостереження. Потім підраховують напрацювання на відмову Т0 і визначають середню кількість відмов за 1000 мото-годин.
При цьому
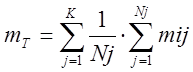(22)
де mij – кількість відмов і-го об’єкту в j-ом інтервалі напрацювання;
Nj – кількість працюючих об’єктів в j-ом інтервалі напрацювання;
K – кількість інтервалів, на які розбивається напрацювання (не менше 6).
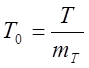(23)
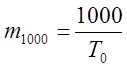(24)
Дата: 2019-05-28, просмотров: 217.
