Показники надійності сільськогосподарської техніки

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Показники надійності сільськогосподарської техніки

Зміст

1 Показники надійності об’єктів

1.1 Ресурс

1.2 γ – процентний ресурс

1.3 Закони розподілення ресурсу

1.4 Нормальний закон розподілення ресурсу

1.5 Розподілення ресурсу за законом Вейбулла

1.6 Визначення закону розподілення ресурсу

1.7 Визначення ресурсу лемеша (приклад)

1.8 Напрацювання на відмову

1.9 Визначення середньої кількості відмов певної складності (приклад)…

1.10 Ймовірність безвідмовної роботи

1.11 Ймовірність безвідмовної роботи машинно-тракторних агрегатів

1.12 Інтенсивність і параметр потоку відмов

2. Властивості ремонтопридатності

3 Показники збереженості

Література

Показники надійності об’єктів

Для промислових виробів, до яких відносяться машини і механізми сільськогосподарського виробництва, номенклатура і характеристика основних показників надійності встановлена ДСТУ 13377 – 75.

Ресурс

У відповідності з цим ДСТУ довговічність машин оцінюється ресурсом – напрацюванням об’єкту від початку експлуатації до граничного стану.

Враховуючи, що машини однієї марки завжди в якійсь мірі відрізняються за своїми вихідними характеристикам і умови використання машин різноманітні, ресурс якої-небудь машини не можна приймати за постійну величину.

Напрацювання конкретної машини до її граничного стану (до виникнення необхідності в капітальному ремонті чи до списання) передбачити неможливо.

Необхідність капітального ремонту машини або будь-яку її відмову в роботі внаслідок дії великої кількості факторів, які безперервно змінюються при експлуатації машини, можна розглянути як події випадкові.

Закономірності випадкових явищ описуються у спеціальному розділі математики – теорії ймовірностей. З врахуванням випадковості появи відмов при експлуатації машин вивчення ряду питань в теорії надійності будується на основі положень теорії ймовірності.

Основною характеристикою випадкової події в теорії ймовірності є її ймовірність. При цьому прийнято рахувати, що ймовірність достовірної події (такої події, яка обов’язково відбудеться) дорівнює одиниці. Ймовірність неможливої події дорівнює нулю. Таким чином, ймовірність будь-якої випадкової події є додатнє число, яке лежить між одиницею і нулем.

Оскільки для встановлення ймовірності випадкової події необхідно зробити нескінченно велику кількість дослідів, то практично ймовірність оцінюється за так званою статичною ймовірністю випадкової події.

Якщо в n дослідах подія, яка нас цікавить виникла m раз, то статична ймовірність цієї події дорівнює відношенню m до n. Вона тим ближче до достовірної величини, чим більше зроблено дослідів.

Приклад. Для оцінки ймовірності появи відмови машини при її роботі на протязі зміни взяли під нагляд 30 таких машин і проводили спостереження на протязі однієї зміни. Якщо при цьому шість машин вийшли з ладу, то шукану ймовірність отримаємо рівною 0,20 (6:30). Ймовірність протилежного випадку події (ймовірність того, що машина даної марки проробить зміну безвідмовно), виходячи з теорії ймовірності, в даному випадку буде дорівнювати

1 – 0,20=0,80.

Крім поняття про випадкову подію, в теорії ймовірності встановлено поняття про випадкову величину.

Випадковою величиною називається величина, яка в результаті досліду може прийняти те чи інше значення, раніш невідоме. Прикладом випадкової величини може бути ресурс об’єкта.

Важливою характеристикою випадкової величини є закон її розподілення, тобто відношення, яке встановлює зв’язок між можливими значенням випадкової величини і відповідними їм ймовірностями.

З теорії ймовірності відомо, що сума ймовірностей усіх можливих значень випадкової величини дорівнює одиниці. Як ця сумарна ймовірність розподілена між окремими значеннями випадкової величини показує закон її розподілення. Відповідно, для того, щоб охарактеризувати ресурс якого-небудь об’єкту, необхідно мати дані про закон його розподілення.

Закон розподілення може бути заданий у вигляді таблиць, у вигляді графіка, або у виді аналітичного виразу. Закон розподілення ресурсу об’єктів, як правило, визначають на основі проведення спеціальних ресурсних випробувань. При цьому беруть для спостереження необхідну кількість об’єктів і статистичною обробкою даних матеріалів випробувань знаходять ймовірність того, що при досягненні об’єктом напрацювання Т, він потребує капітального ремонту чи списання.

В процесі випробувань контролюється технічний стан кожного об’єкта. Якщо граничний стан об’єкта настає, наприклад, при величині зносу базового елемента, яка дорівнює граничному значенню, то за результатами спостережень можна побудувати графік, що відображає процес спрацювання кожного об’єкта в процесі його експлуатації (рис. 1, а).

Для кожного об’єкта залежність зносу його елементів від експлуатаційного напрацювання Т представляє собою випадкову функцію. Отримати відомості про ресурс конкретного об’єкта до проведення його випробувань практично неможливо. Результати завершених експлуатаційних випробувань партії однотипних об’єктів дозволяють знайти закон розподілення ресурсу об’єкта і побудувати графік, який показує ймовірність того, що на протязі заданого напрацювання Т виникає потреба в капітальному ремонті об’єкта (рис. 1, б). З цього графіка видно, яка частина усіх випробуваних об’єктів потребує капітального ремонту чи заміни при відповідному напрацюванні Т. Ординату будь-якої точки графіка F(T) знаходять як відношення кількості об’єктів m, які втратили ресурс при досягненні напрацювання Т, до загальної кількості об’єктів n, які приймають участь у випробуванні, тобто:

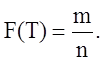(1)

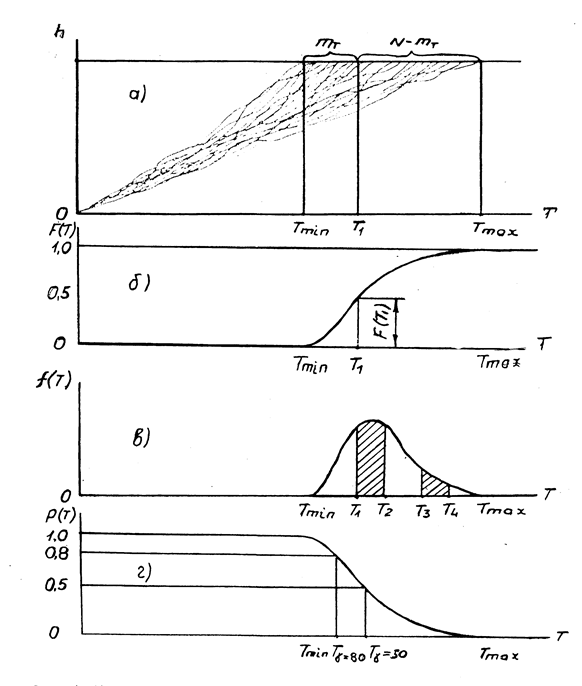
Рис. 1. Визначення технічного ресурсу об’єкта за результатами експлуатаційних випробувань.

Графік F(T) називають законом розподілення ресурсу об’єкту, що випробується. Нижче цього графіка, на рис. 1,в зображений цей же закон розподілення у вигляді графіка швидкості зміни функції F(T).

Такий графік називають щільністю розподілу ресурсу. За його видом можна судити про ймовірність втрати об’єктом ресурсу в різних діапазонах напрацювання. Як видно з цього графіка, максимальна ймовірність втрати об’єктом ресурсу спостерігається в інтервалі Т₁...Т₂. В такому ж інтервалі напрацювання Т₃...Т₄ об’єкти також будуть втрачати свій ресурс, але таких об’єктів буде значно менше, ніж в діапазоні Т₁...Т₂.

На рис. 1, г зображений також закон розподілення ресурсу, але цей графік показує ймовірність того, що при досягненні напрацювання Т граничний стан об’єкта ще не настане. Ордината кожної точки даного графіка визначиться за формулою:

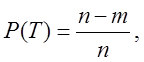(2)

Таким чином, ордината дорівнює відношенню кількості об’єктів, які знаходяться в працездатному стані при досягненні напрацювання Т, до загальної кількості об’єктів n, що випробуються.

Слід зазначити, що при будь-якому напрацюванні F(T) + Р(T)=1. Графік Р(T) ще називають кривою зменшення ресурсу.

Всі три графіки взаємопов’язані і, якщо є один з них, можна побудувати два інших. Будь-який з цих графіків містить вичерпну інформацію про ресурс об’єкта даного виду і дозволяє знайти середнє значення ресурсу, визначити середньоквадратичне відхилення ресурсу, його γ-процентний ресурс.

Середнє значення ресурсу за результатами випробувань знаходиться за формулою:

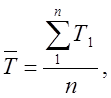(3)

де

Т₁ – ресурс і-го об’єкта (і-1, 2, 3,...,n);

n – кількість об’єктів, які випробовуються.

Середнє квадратичне відхилення ресурсу σ, яким оцінюється розсіювання ресурсу відносно його середнього значення, підраховується за формулою:

σ 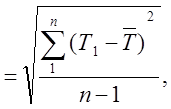(4)

Середньоквадратичне відхилення ресурсу має таку ж розмірність, що і ресурс. Безрозмірною оцінкою розсіювання ресурсу є коефіцієнт варіації ресурсу V.

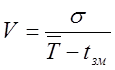, (5)

де t_зм – найменше значення ресурсу або величина зміщення початку розсіювання.

Повною, вичерпною характеристикою ресурсу будь-якого об’єкта є закон його розподілення. Ресурс технічних об’єктів може бути оцінений також за

γ-процентним ресурсом;

1.2 γ-процентний ресурс

γ-процентний ресурс – це напрацювання, на протязі якого об’єкт не досягає граничного стану з заданою ймовірністю γ у процентах. Для об’єкту даного виду із збільшенням γ, величина його γ-процентного ресурсу, зменшується (рис. 1г).

В машинобудуванні прийнято оцінювати ресурс виробів значенням 90 %-го γ-ресурсу (Т_γ=90). Якщо, наприклад, для якогось виробу Т_γ=80=5000 мото-годин, то це означає, що при випробуванні достатньо великої партії виробів цього виду при напрацюванні 5000 мото-годин. 90% цих виробів ще залишаться в працездатному стані і не будуть вимагати капітального ремонту чи списання, а 10% - до цього напрацювання втратять ресурс.

Перевагою оцінки ресурсу виробу через його γ-процентний ресурс є суттєве скорочення тривалості випробувань для його визначення. Якщо для виявлення закону розподілення ресурсу, для отримання 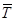, σ і V необхідно вести спостереження до вичерпання свого ресурсу самим довговічним об’єктом з усієї партії об’єктів, що випробуються, то для визначення, наприклад, 90%-го γ-ресурсу тривалість випробувань буде визначатись втратою ресурсу тільки першими 10% об’єктів (їх напрацюванням до граничного стану).

Для тракторів і їх агрегатів, які пройшли капітальний ремонт, в теперішній час встановлені нормативи на їх 90-ти процентний γ-ресурс. Якість ремонту цих об’єктів, з точки зору їх післяремонтної довговічності, визначається встановленням фактичної величини Т_γ=80 і порівнянням його з нормативним значенням.

Закони розподілення ресурсу

Ресурс об’єкту як випадкова величина може бути розподілений по одному з законів розподілення, які вивчаються в теорії ймовірності. Найбільш часто ресурс об’єкту розподіляється за нормальним законом, або за законом Вейбулла.

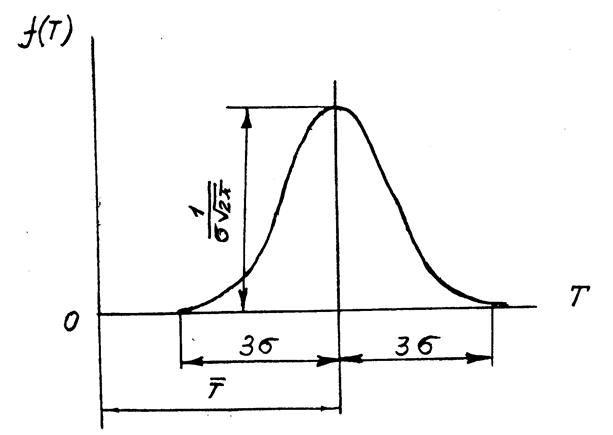
Рис. 2. Функція щільності розподілення ресурсу при нормальному законі розподілення.

Напрацювання на відмову

Основним показником, який оцінює безвідмовність сільськогосподарської техніки є напрацювання на відмову – Т_в.

Напрацювання на відмову – середнє напрацювання відновлюваного об’єкту між двома відмовами. Цей показник визначається за результатами спостережень за формулою:

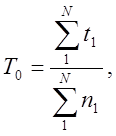(21)

де N – кількість об’єктів, які взяті на спостереження;

t₁ – напрацювання і-го об’єкту за час спостереження;

n₁ – кількість відмов і-го об’єкту за час спостереження.

Згідно ДСТУ 70/23.2.8 – 79 “Випробування сільськогосподарської техніки. Трактори і машини сільськогосподарські. Надійність. Збір і обробка інформації”, відмови складних виробів (тракторів, комбайнів і їх агрегатів) по трудомісткості усунення поділяються на 3 групи (найбільш складні – 3-ої групи). При оцінці безвідмовності цих об’єктів величина напрацювання на відмову повинна визначатися шляхом обробки результатів окремо по кожній групі складності.

Для тракторів і їх агрегатів, які пройшли капітальний ремонт, в якості їх безвідмовності прийнято рахувати кількість відмов кожної групи складності за кожні 1000 мото-годин роботи двигуна. В нормативах надійності капітально відремонтованих тракторів вказано допустима середня кількість відмов тієї чи іншої групи складності за кожну тисячу мото-годин роботи двигуна. Якість ремонту цих об’єктів з точки зору їх післяремонтної безвідмовності визначається встановленням фактичного середнього числа відмов кожної з трьох груп складності на тисячу мото-годин і порівнюємо їх з нормативними значеннями.

Для визначення фактичного середнього числа відмов кожної з трьох груп складності на тисячу мото-годин спочатку за результатами випробувань знаходять середнє кількість відмов даного виду m_T у об’єкта за напрацювання Т, на протязі якого проводились спостереження. Потім підраховують напрацювання на відмову Т₀ і визначають середню кількість відмов за 1000 мото-годин.

При цьому

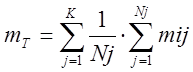(22)

де m_ij – кількість відмов і-го об’єкту в j-ом інтервалі напрацювання;

N_j – кількість працюючих об’єктів в j-ом інтервалі напрацювання;

K – кількість інтервалів, на які розбивається напрацювання (не менше 6).

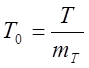(23)

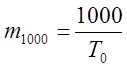(24)

Показники збереженості

Пристосованість машин до зберігання, можна оцінювати через питому вартість або питому трудомісткість зберігання. Ці показники визначаються за наступними залежностями

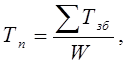(34)

де ∑С_зб і ∑Т_зб – відповідно сумарні затрати (грн.) і трудомісткість зберігання (люд-год) за рік використання машини;

W – напрацювання машин за цей період.