Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ

 

 

Семестровое задание

И методические указания к решению задач

 

 

Челябинск

Издательство ЮУрГУ

2000

 

УДК

ББК

    Габрин К.Э., Математические методы и модели: Семестровое задание и методические рекомендации к решению задач. – Челябинск: Издательство ЮУрГУ, 2000. – 39 с.

    Приведены задачи семестрового задания, методические указания к их решению, примеры вычислений, рекомендуемая литература и приложения.

    Пособие предназначено для студентов специальностей 060811, 061101, 061120.

Табл. 12, прилож. 4, список лит. – 13 назв.

 

 

Одобрено учебно-методической комиссией факультета «Экономика и управление».

 

 

Рецензент: Никифоров К.В.

Задача 1

Многофакторный регрессионный и корреляционный анализ

 

Варианты задач с 1 по 25 с указанием результативного y и факторных x₁, x₂ признаков приведены в табл. 1.

 

По выборочным данным, представленным в табл. 2 и табл. 3, исследовать на основе линейной регрессионной модели зависимость результативного признака от показателей производственно-хозяйственной деятельности предприятий.

Таблица 1

Варианты задач

№ вар.	Результативный признак	Факторные признаки	№ вар.	Результативный признак	Факторные признаки
1	y1	x1,x3	14	y3	x1,x14
2	y2	x1,x5	15	y2	x5,x9
3	y2	x1,x7	16	y3	x8,x10
4	y2	x1,x11	17	y3	x7,x14
5	y2	x1,x10	18	y3	x3,x6
6	y1	x3,x4	19	y3	x1,x14
7	y2	x3,x11	20	y1	x2,x6
8	y2	x11,x5	21	y1	x3,x7
9	y1	x3,x5	22	y2	x5,x8
10	y2	x11,x6	23	y2	x9,x10
11	y2	x1,x6	24	y3	x4,x11
12	y2	x1,x12	25	y3	x1,x12
13	y2	x1,x2

 

Таблица 2

Обозначения и наименование показателей

производственно-хозяйственной деятельности предприятий

Обозначение показателя	Наименование показателя
y1	Производительность труда, тыс.руб./чел.
y2	Индекс снижения себестоимости продукции
y3	Рентабельность
x1	Трудоемкость единицы продукции
x2	Удельный вес рабочих в составе ППР
x3	Удельный вес покупных изделий
x4	Коэффициент сменности оборудования, смен
x5	Премии и вознаграждения на одного работника ППР, тыс.руб.
x6	Удельный вес потерь от брака,%
x7	Фондоотдача активной части ОПФ, руб./руб.
x8	Среднегодовая численность ППР, чел.
x9	Среднегодовая стоимость ОПФ, млн.руб.
x10	Среднегодовой фонд заработной платы ППР
x11	Фондовооруженность труда, тыс.руб./чел.
x12	Оборачиваемость нормируемых оборотных средств, дн.
x13	Оборачиваемость ненормируемых оборотных средств, дн.
x14	Непроизводительные расходы, тыс.руб.

 

Таблица 3

Исходные данные для расчета

№	y1	y2	y3	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11	x12	x13	x14
1	9,4	62	10,6	0,23	0,62	0,4	1,35	0,88	0,15	1,91	7394	39,53	14257	5,35	173,9	11,88	28,13
2	9,9	53,1	9,1	0,43	0,76	0,19	1,39	0,57	0,34	1,68	11586	40,41	22661	3,9	162,3	12,6	17,55
3	9,1	56,5	23,4	0,26	0,71	0,44	1,27	0,7	0,09	1,89	7801	37,02	14903	4,88	101,2	8,28	19,52
4	5,5	30,1	9,7	0,43	0,74	0,25	1,1	0,84	0,05	1,02	6371	41,08	12973	5,65	177,8	17,28	18,13
5	6,6	18,1	9,1	0,38	0,72	0,02	1,23	1,04	0,48	0,88	4210	42,39	6920	8,85	93,2	13,32	21,21
6	4,3	13,6	5,4	0,42	0,68	0,06	1,39	0,66	0,41	0,62	3557	37,39	5736	8,52	126,7	17,28	22,97
7	7,4	89,8	9,9	0,30	0,77	0,15	1,38	0,86	0,62	1,09	14148	101,7	26705	7,19	91,8	9,72	16,38
8	6,6	76,6	19,1	0,37	0,77	0,24	1,35	1,27	0,5	1,32	15118	81,32	28025	5,38	70,6	8,64	16,16
9	5,5	32,3	6,6	0,34	0,72	0,11	1,24	0,68	1,2	0,68	6462	59,92	11049	9,27	97,2	9,0	20,09
10	9,4	199	14,2	0,23	0,79	0,47	1,4	0,86	0,21	2,3	24628	107,3	45893	4,36	80,3	14,76	15,98
11	5,7	90,8	8	0,41	0,71	0,2	1,28	0,45	0,66	1,43	1948	80,83	36813	4,16	128,5	10,44	22,76
12	5,2	82,1	17,5	0,41	0,79	0,24	1,33	0,74	0,74	1,82	18963	59,42	33956	3,13	94,7	14,76	15,41
13	10,0	76,2	17,2	0,22	0,76	0,54	1,22	1,03	0,32	2,62	9185	36,96	17016	4,02	85,3	20,52	19,35
14	6,7	37,1	12,9	0,31	0,79	0,29	1,35	0,96	0,39	1,24	6391	37,21	11688	5,82	85,3	7,92	14,63
15	9,4	51,6	13,2	0,24	0,70	0,56	1,2	0,98	0,28	2,03	6555	32,87	12243	5,01	116,6	18,72	22,62

Таблица 4

Исходная информация для анализа и результаты расчета

Исходная информация

Результаты расчета

№ x_i1 x_i2 y_i y*_i (y*_i)² e_i=y_i-y*_i (e_i)² d_i= e_i / y*_i 1 3 1,8 2,1 2,31572 5,36255 -0,21572 0,04653 -0,09315 2 4 1,5 2,8 3,48755 12,16300 -0,68755 0,47273 -0,19714 3 5 1,4 3,2 4,35777 18,99015 -1,15777 1,34043 -0,26568 4 5 1,3 4,5 4,50907 20,33171 -0,00907 0,00008 -0,00201 5 5 1,3 4,8 4,50907 20,33171 0,29093 0,08464 0,064521 6 5 1,5 4,9 4,20647 17,69439 0,69353 0,48098 0,164872 7 6 1,6 5,5 4,77408 22,79184 0,72592 0,52696 0,152054

 

Окончание табл. 4

	Исходная информация			Результаты расчета
№	xi1	xi2	yi	y*i	(y*i)2	ei=yi-y*i	(ei)2	di= ei / y*i
8	7	1,2	6,5	6,09821	37,18816	0,40179	0,16144	0,065887
9	15	1,3	12,1	11,6982	136,84905	0,40175	0,16140	0,034343
10	20	1,2	15,0	15,4441	238,52177	-0,44415	0,19727	-0,02876
	Сред. знач.			S=	530,22437	S=	3,47247
	7,5	1,41	6,14
y*i – значения, вычисленные по уравнению регрессии
ei – абсолютные ошибки аппроксимации
di – относительные ошибки аппроксимации

Решение

 

1. Определение вектора b оценок коэффициентов

уравнения регрессии

 

Расчет оценок коэффициентов уравнения регрессии y*=b₀+b₁x₁+b₂x₂ производится по уравнению b=(X^TX)^–1X^TY:

 

	n	Sxi1	Sxi2		10	75	14,1
XTX =	Sxi1	Sx2i1	Sxi1xi2	=	75	835	100,4
	Sxi2	Sxi1xi2	Sx2i2		14,1	100,4	20,21

 

	Syi		61,4		b0		2,88142
XTY =	Sxi1yi	=	664,5	b =	b1	=	0,71892
	Sxi2yi		82,23		b2		-1,51303

Таким образом, оценка уравнения регрессии примет вид

 

y*=2,88142+0,71892x₁-1,51303x₂.

 

2. Проверка значимости уравнения y*=2,88142+0,71892x₁-1,51303x₂.

 

а) Q_R=(Xb)^T(Xb)=Sy*_i =530,224365;

б) Q_ост=(Y-Xb)^T(Y-Xb)= Se²_i =3,472465;

в) несмещенная оценка остаточной дисперсии:

S*²= Q_ост/(n-3)=3,472465 / 7 = 0,496066;

г) оценка среднеквадратичного отклонения:

S*= 0,7043195;

д) проверяем на уровне a=0,05 значимость уравнения регрессии, т.е. гипотезу H₀: b=0 (b₀=b₁=b₂=0). Для этого вычисляем

 

F_набл=(Q_R/(k+1))/(Q_ост/(n-k-1))=(530,224365 / 3))/(3,472465 / 7))=356,32776.

 

Далее по таблице F-распределения для a=0,05, n₁=k+1=3, n₂=n-k-1=7 находим F_кр=4,35. Так как F_набл>F_кр (356,32776>4,35), то гипотеза H₀ отвергается с вероятностью ошибки 0,05. Т.о. уравнение является значимым.

 

3. Проверка значимости отдельных коэффициентов регрессии

 

а) Найдем оценку ковариационной матрицы вектора b:

 

	5,52259	-0,08136	-3,44878
S*(b)=S*2(XTX)–1=0,496066(XTX)–1=	-0,08136	0,00267	0,04348
	-3,44878	0,04348	2,21466

 

Так как на главной диагонали ковариационной матрицы находятся дисперсии коэффициентов уравнения регрессии, то получим следующие несмещенные оценки этих дисперсий:

 

S*²_b0=5,52259; S*²_b1=0,00267; S*²_b0=2,21466;

S*_b0=2,35002; S*_b1=0,05171; S*_b2=1,48818.

Найдем оценку корреляционной матрицы вектора b. Элементы этой матрицы определяются по формуле:

r_j-1l-1=cov*(b_j-1,b_l-1)/(S*_bj-1S*_bl-1),

где cov*(b_j-1,b_l-1) – элементы матрицы S*(b), стоящие на пересечении j-той строки и l -того столбца ( j,l =1,2,3).

Корреляционная матрица вектора b имеет вид:

 

	1	-0,66955	-0,98614
R*(b)=	-0,66955	1	0,56504
	-0,98614	0,56504	1

 

Далее, для проверки значимости отдельных коэффициентов регрессии, т.е. гипотез H₀: b_m=0 (m=1,2), по таблицам t-распределения для a=0,05, n=7 находим t_кр=2,365. Вычисляем t_набл для каждого из коэффициентов регрессии по формуле t_набл(b_j)=b_j/S*_bj:

 

t_набл(b₁)=b₁/S*_b1=0,71892/0,05171=13,903

t_набл(b₂)=b₂/S*_b2=1,51303/1,48818=1,01667.

 

Так как t_набл(b₁) > t_кр (13,903 > 2,365), t_набл(b₂) < t_кр (1,01667< 2,365), то коэффициент регрессии b₁¹0, а коэффициент регрессии b₂=0. Следовательно переходим к алгоритму пошагового регрессионного анализа.

 

4. Пошаговый регрессионный анализ

 

Будем рассматривать оценку нового уравнения регрессии вида

y*=b’₀+b’₁x₁. Вектор оценок b’ определим по формуле b=(X^T ¢ X ¢ )^–1X^T ¢ Y, где

 

	n	Sxi1		10	75
XT¢X¢ =	Sxi1	Sx2i1	=	75	835

 

	Syi		61,4		b’0		0,52534
XT¢Y¢ =	Sxiyi	=	664,5	b¢ =	b’1	=	0,74861

 

Таким образом, оценка уравнения регрессии примет вид:

y*=0,52534+0,74861x₁.

Повторив далее вычисления по пп 2 и 3, определяем, что новая оценка уравнения регрессии и его коэффициент значимы при a=0,05.

 

5. Нахождение матрицы парных коэффициентов корреляции

(на примере без исключения переменной)

а) находим вектор средних:

X _ср=(x_1ср; x_2ср; y_ср)=(7,5; 1,41; 6,14);

б) находим вектор среднеквадратических отклонений S=(s₁; s₂; s_y) по формуле s_j=([S(x_ij - x_jср)²]/n)^0,5, i=1…n:

S=(5,22; 0,18; 3,91);

в) формируем корреляционную матрицу

 

	1	r12	r1y
R=	r21	1	r2y
	ry1	ry2	1

 

где r₁₂=r₂₁=[(x₁x₂)_ср-x_1срx_2ср]/(s₁s₂), r_yj=r_jy=[(x_jy)_ср-x_jсрy_ср]/(s_js_y):

 

	1	-0,565	0,997
R=	-0,565	1	-0,612
	0,997	-0,612	1

 

6. Расчет оценок частных коэффициентов корреляции

 

Оценки частных коэффициентов корреляции определяются по формулам:

 

r_12/y=(r₁₂-r_1yr_2y)/[(1-r_1y²)(1-r_2y²)]^0,5 =0,738;

r_1y/2=(r_1y-r₁₂r_y2)/[(1-r₁₂²)(1-r_y2²)]^0,5 =0,998;

r_2y/1=(r_1y-r₁₂r_y2)/[(1-r₁₂²)(1-r_y2²)]^0,5 =-0,762.

 

Составим матрицу частных коэффициентов корреляции:

 

1	0,738	0,998
0,738	1	–0,762
0,998	–0,762	1

 

Следует иметь в виду, что частный коэффициент корреляции может резко отличаться от соответствующего парного коэффициента и даже иметь противоположный знак. Любой из частных коэффициентов может быть равен нулю, в то время, как парный – отличен от нуля.

В данном примере r_12/y=0,738, а r₁₂=-0,565. Такое различие вызвано тесной связью объема валовой продукции (x₁) и себестоимостью товарной продукции (y): r_1y=0,997. В случае независимости величин частный и парный коэффициенты корреляции равны нулю.

7. Проверка значимости парных и частных

коэффициентов корреляции

 

Проверка осуществляется с помощью таблиц t-распределения Стьюдента.

Для r₁₂: |t_набл|=|(10-2)^0,5(-0,565)/(1-(-0,565)²)^0,5|=1,93683<t_кр(8;0,05)=2,306; гипотеза H₀: r₁₂=0 принимается с вероятностью ошибки 0,05; отвергается с вероятностью ошибки 0,1 (|t_набл|=1,93683>t_кр(8;0,1)=1,86).

Для r_2y: |t_набл|=|(10-2)^0,5(-0,612)/(1-(-0,612)²)^0,5|=2,20621<t_кр(8;0,05)=2,306; гипотеза H₀: r_2y=0 принимается с вероятностью ошибки 0,05; отвергается с вероятностью ошибки 0,1 (|t_набл|=1,93683 > t_кр(8;0,1)=1,86).

Для r_1y: |t_набл|=|(10-2)^0,50,997/(1-0,997²)^0,5|=36,43263>t_кр(8;0,05)=2,306; гипотеза H₀: r_1y=0 отвергается с вероятностью ошибки 0,05.

Для r_12/y: |t_набл|=|(n-3)^0,50,738/(1-0,738²)^0,5|=2,893542>t_кр(7;0,05)=2,365; гипотеза H₀: r_12/y=0 отвергается с вероятностью ошибки 0,05.

Для r_1y/2: |t_набл|=|(n-3)^0,50,998/(1-0,998²)^0,5|=41,77023>t_кр(7;0,05)=2,365; гипотеза H₀: r_1y/2=0 отвергается с вероятностью ошибки 0,05.

Для r_2y/1: |t_набл|=|(n-3)^0,5(-0,762)/(1-(-0,762)²)^0,5|=3,11324>t_кр(7;0,05)=2,365; гипотеза H₀: r_2y/1=0 отвергается с вероятностью ошибки 0,05.

 

 

8. Расчет оценок множественных коэффициентов

корреляции и детерминации

 

Оценки множественных коэффициентов корреляции детерминации рассчитываются по формулам:

r_y/12 = (r_y1²+ r_y2²+ 2r_y1r_y2r₁₂)/(1-r₁₂²)(1-r_y2²)]^0,5 =0,999;

r_y/12² =0,999²=0,997.

 

9. Проверка значимости множественных коэффициентов

корреляции и детерминации

 

Проверим гипотезу H₀: r²_y/12 =0 по F-критерию. Наблюдаемое значение находится по формуле:

F_набл= [r²_y/12/(k-1)]/[(1-r_y/12)/(n-k)]=[0,997/(3-1)]/[(1-0,997)/(10-3)]=1163.

По таблице F-распределения для a=0,05, n₁=k-1=2, n₂=n-k=7 находим F_кр=4,74. Так как F_набл>F_кр, то гипотеза о равенстве r²_y/12 =0 отвергается.

Аналогично осуществляется проверка гипотезы r_y/12=0 (в данном примере опущено).

Тем самым доказана значимость множественного коэффициента корреляции, что говорит о наличии зависимости y от x₁ и x₂, т.е. себестоимость действительно зависит от объема валовой продукции и производительности труда.

 

Литература к задаче 1

 

1. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: Исследование зависимостей.–М.:Финансы и статистика, 1985

2. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: Основы моделирования и первичной обработки данных.–М.:Финансы и статистика, 1983

3. Львовский Е.Н. Статистические методы построения эмпирических формул.–М.:Высш.шк., 1988.

4. Шепелев И.Г. Математические методы и модели управления в строительстве.–М.:Высшая школа, 1980.

 

Задача 2

 

Динамическое программирование

 

Для увеличения объемов выпуска пользующейся повышенным спросом продукции, изготавливаемой тремя предприятиями, выделены капитальные вложения в объеме 700 млн.руб. Использование i-тым предприятием x_i млн. руб. из указанных средств обеспечивает прирост выпуска продукции, определяемый значением нелинейной функции f_i(x_i).

Найти распределение капитальных вложений между предприятиями, обеспечивающее максимальное увеличение выпус6ка продукции.

Исходные данные приведены в таблицах 5 и 6.

Таблица 5

Исходные данные

Объем кап.вложений xi, млн.руб.	Прирост выпуска продукции fi(xi), млн.руб.
	Предприятие 1	Предприятие 2	Предприятие 3
0	0	0	0
100	а	50	40
200	50	80	d
300	b	90	110
400	110	150	120
500	170	с	180
600	180	210	220
700	210	220	240

 

Таблица 6

Варианты исходных данных

Вариант	a	b	c	d
1	30	90	190	50
2	20	80	160	70
3	35	100	190	60
4	40	110	180	90
5	30	100	190	60

 

Окончание табл. 6

Вариант	a	b	c	d
6	35	80	160	70
7	40	80	160	70
8	40	100	190	60
9	30	110	160	90
10	40	110	190	90
11	20	100	190	60
12	20	80	180	60
13	35	110	190	50
14	40	90	160	50
15	30	90	190	90
16	35	90	160	70
17	40	90	190	50
18	20	90	150	90
19	20	80	190	60
20	20	110	160	70
21	40	90	190	60
22	30	110	190	55
23	35	90	180	70
24	45	85	170	90
25	40	85	170	50

В задаче необходимо:

1. Составить рекуррентное соотношение Беллмана в виде функциональных уравнений.

2. Используя рекуррентные соотношения и исходные данные определить сначала условно оптимальные, а затем оптимальные распределения капиталовложений между предприятиями.

 

Литература к задаче 2

1. Вентцель Е.С. Исследование операций: задачи, принципы, методология.– М.:Наука. Гл. ред. физ.-мат. лит.,1988.

2. Вентцель Е.С. Основы исследования операций.– М.: Советское радио, 1972.

3. Габасов Р.Ф., Кириллова Ф.М. Основы динамического программирования.– Минск:Изд-во БГУ,1975.

4. Исследование операций в экономике: Учеб. пособие для вузов по экон. специальностям / Под ред. Н.Ш.Кремера.– М.: Банки и биржи,1997.

5. Калихман И.Л., Войтенко М.А. Динамическое программирование в примерах и задачах.– М.: Высшая школа,1979.

 

Задача 3

Марковские случайные процессы

 

Исходные данные задачи.

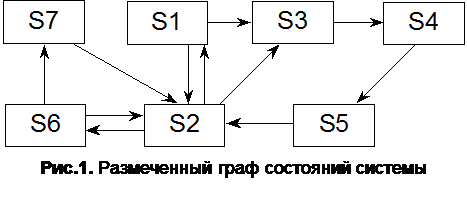Размеченный граф состояний системы представлен на рис. 1.

 

Заданы следующие состояния системы.

1. S1 – исправна, функционирует (загружена).

2. S2 – исправна, не функционирует (не загружена).

3. S3 – неисправна, факт неисправности устанавливается.

4. S4 – факт неисправности установлен, ведется поиск неисправности.

5. S5 – ремонтируется.

6. S6 – ведется профилактический осмотр.

7. S7 – ведется профилактический ремонт.

Обозначение исходных данных для расчета интенсивностей потоков событий приведено в таблице 7.

Таблица 7

Обозначение исходных данных

Наименование	Обозначение	Размерность
Среднее время наработки на отказ	T1	сутки
Среднее время функционирования системы	T2	часы
Среднее время простоя исправной системы	T3	часы
Среднее время установление факта неисправности	T4	часы
Среднее время поиска неисправности	T5	часы
Среднее время устранения неисправности (ремонта)	T6	часы
Периодичность профилактического осмотра	Один раз в T7 дней	сутки
Средняя продолжительность проф. осмотра	T8	часы
Средняя продолжительность проф. ремонта	T9	часы

 

    В задаче требуется определить следующее. Окупит ли себя увеличение дохода, связанное с уменьшением T_i в n_j раз (n₁=2; n₂=3), если при этом возникают дополнительные затраты в размере 0,5n₁D_i, и 0,75n₂D_i, где D_i – убыток, приносимый системой в соответствующем времени T_i состоянии.

Варианты исходных данных приведены в табл. 8.

 

Таблица 8

Варианты исходных данных

№	Значения Ti									Доход Di в единицу времени в зависимости от состояния системы (руб.)
вар.	Т1	Т2	Т3	Т4	Т5	Т6	Т7	Т8	Т9	S1	S2	S3	S4	S5	S6	S7	Тi
1	20	6	0,3	0,4	0,9	1,3	22	0,6	6	207	-23	-5	-4	-23	-8	-9	3
2	23	4	0,4	0,2	0,6	1,7	38	0,9	6	229	-24	-6	-3	-15	-11	-11	7
3	24	8	0,3	0,4	0,9	1	22	0,9	7	207	-21	-5	-2	-23	-7	-9	7
4	20	4	0,3	0,3	0,6	1,3	35	1	7	247	-20	-4	-7	-22	-7	-8	3
5	20	4	0,1	0,6	0,9	2,1	32	0,6	6	208	-20	-6	-6	-17	-11	-8	3
6	21	4	0,4	0,5	0,7	1,2	44	0,8	6	297	-22	-2	-6	-10	-7	-9	3
7	20	4	0,3	0,5	0,6	2	23	0,5	5	228	-19	-3	-4	-21	-7	-8	7
8	18	4	0,4	0,2	0,6	0,9	24	0,9	6	214	-24	-2	-7	-25	-9	-9	7
9	19	5	0,1	0,3	0,7	1	42	0,9	5	280	-21	-6	-7	-15	-9	-9	7
10	21	8	0,1	0,6	0,5	1,5	40	1	7	226	-20	-6	-3	-18	-9	-11	3
11	18	8	0,2	0,6	1	0,8	48	0,8	6	214	-20	-6	-7	-16	-8	-8	7
12	21	4	0,2	0,6	1	0,9	32	0,8	5	277	-23	-5	-4	-13	-7	-10	3
13	21	4	0,4	0,5	0,6	2,2	46	0,7	6	295	-23	-4	-2	-11	-10	-10	7
14	18	4	0,1	0,3	0,8	0,8	20	0,6	5	264	-22	-6	-4	-24	-8	-8	7

 

Окончание табл. 8

 

№	Значения Ti									Доход Di в единицу времени в зависимости от состояния системы (руб.)
вар.	Т1	Т2	Т3	Т4	Т5	Т6	Т7	Т8	Т9	S1	S2	S3	S4	S5	S6	S7	Тi
15	19	6	0,4	0,3	0,9	2,1	29	0,9	7	208	-20	-5	-3	-17	-10	-10	7
16	22	4	0,3	0,2	0,5	0,9	35	0,8	5	255	-24	-4	-7	-22	-8	-9	3
17	18	8	0,4	0,5	1	0,8	33	0,5	7	207	-21	-2	-4	-15	-10	-11	3
18	20	5	0,4	0,5	1	1,9	22	0,6	5	207	-21	-5	-4	-25	-8	-9	7
19	21	5	0,1	0,6	0,9	1,3	40	0,9	5	235	-18	-2	-3	-11	-10	-11	3
20	18	5	0,2	0,3	0,8	1,2	43	0,5	6	293	-23	-2	-5	-21	-7	-11	7
21	25	4	0,2	0,2	0,6	1,2	45	0,7	7	277	-19	-5	-4	-13	-11	-10	3
22	18	5	0,2	0,5	0,8	1	34	0,8	6	210	-21	-6	-5	-20	-9	-11	3
23	19	8	0,3	0,6	0,8	2	33	1	6	232	-25	-2	-3	-14	-11	-12	7
24	22	8	0,1	0,3	1	1,9	29	0,9	7	238	-24	-2	-2	-21	-10	-10	3
25	24	5	0,1	0,6	0,5	0,8	41	1	7	266	-22	-5	-4	-15	-11	-12	7

 

Методические указания к решению задачи 3

 

1. Расчитываются интенсивности потоков событий.

2. Составляются уравнения Колмогорова.

3. Находится решение уравнений Колмогорова (вручную и численно).

4. Вычисляются финальные вероятности состояний системы.

5. Используя значения финальных вероятностей состояний определяется доход, приносимый системой в единицу времени.

6. Определяется изменение дохода при уменьшении T_i. Для этого пересчитывается интенсивность соответствующенго потока событий, находится новое решение уравнений Колмогорова и новые финальные вероятности. После этого определяется новое значение дохода, определяется его разница с предыдущим и результат сопоставляется с произведенными дополнительными затратами.

 

Численное решение уравнений Колмогорова производится в среде MS EXCEL. Текст программы на языке VB для EXCEL приведен в приложении 2. Оформление рабочего листа – в приложении 3.

 

Литература к задаче 3

 

1. Вентцель Е.С. Исследование операций: задачи, принципы, методология.–М.:Наука. Гл. ред. физ.-мат. лит.,1988.

2. Вентцель Е.С. Основы исследования операций.– М.: Советское радио, 1972.

3. Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения.– М.: Наука, 1991.

4. Ярлыков М.С., Миронов М.А. Марковская теория оценивания случайных процессов.-М.:Радио и связь, 1993.

 

Задача 4

Метод Монте-Карло

 

Рассчитать нетто-ставку тарифа при страховании строительства здания по исходным данным, приведенным в табл.9, табл.10. и на рис.2.

Таблица 9

Обозначения исходных данных

Наименование	Обозначение
Заданная точность	e
Вероятность попадания при испытаниях в зону, ограниченную заданной точностью	Y
Показатель качества проектирования	mп
Закон распределения xп	fп
Показатель предполагаемого качества материалов	mм
Закон распределения xм	fм
Показатель предполагаемого качества выполнения СМР	mс
Закон распределения xс	fс
Число этажей объекта	m
Число несущих конструкций на этаже	n
Число несущих конструкций на нулевом цикле	v
Класс подверженности внешним факторам риска	K
Вероятность внешнего фактора 1	P1
Вероятность внешнего фактора 2	P2
Вероятность внешнего фактора 3	P3

Таблица 10

Варианты исходных данных

№	e	Y	mп	fп	mм	fм	mс	fс	m	n	v	K	P1	P2	P3
1	0,001	0,9999	0,85	2	0,89	3	0,80	2	6	6	6	4	6,2E-04	6,0E-05	1,3E-06
2	0,001	0,999	0,92	3	-	4	-	4	9	3	7	1	5,6E-04	2,8E-05	1,7E-06
3	0,001	0,99999	0,88	1	0,87	2	0,82	3	16	3	7	4	0	3,0E-05	6,9E-06
4	0,0015	0,99999	-	4	0,82	3	0,90	2	24	5	4	2	6,0E-04	3,2E-05	8,7E-06
5	0,0015	0,9999	-	4	0,81	3	0,90	3	48	5	4	5	7,6E-04	0	3,4E-06
6	0,0015	0,9998	0,90	1	0,90	2	-	4	9	5	8	3	7,9E-04	3,8E-05	6,9E-06
7	0,001	0,9999	0,83	3	0,82	2	0,68	2	6	2	5	4	6,0E-04	7,2E-05	5,6E-06
8	0,0018	0,9999	0,87	1	0,82	1	0,68	1	48	8	8	1	5,3E-04	2,1E-05	4,2E-06
9	0,0015	0,9998	0,85	3	0,83	2	0,75	1	22	8	4	2	8,2E-04	3,3E-05	5,8E-06
10	0,001	0,9998	0,86	2	0,86	3	-	4	9	3	8	3	0	6,0E-05	3,0E-06
11	0,0015	0,9999	0,78	3	0,88	3	0,89	1	10	3	5	2	7,3E-04	5,4E-05	3,5E-06
12	0,0015	0,9999	0,84	1	-	4	0,87	1	6	7	4	5	7,8E-04	3,3E-05	2,3E-06

 

 

Окончание табл. 10

№	e	Y	mп	fп	mм	fм	mс	fс	m	n	v	K	P1	P2	P3
13	0,0015	0,9998	0,80	3	0,80	3	-	4	9	8	6	1	6,9E-04	3,4E-05	7,2E-06
14	0,001	0,9998	-	4	0,88	3	0,83	1	16	5	7	5	5,4E-04	5,5E-05	2,3E-06
15	0,0015	0,9998	0,73	2	0,81	1	0,82	3	24	2	5	5	7,0E-04	4,2E-05	4,5E-06
16	0,0012	0,9999	0,88	3	0,79	3	-	4	48	2	7	3	6,9E-04	0	8,3E-06
17	0,0015	0,9998	0,87	2	-	4	0,87	2	9	7	6	3	7,0E-04	7,2E-08	7,9E-06
18	0,001	0,9996	0,73	3	0,91	2	0,76	2	6	2	4	2	5,2E-04	7,4E-05	2,9E-06
19	0,0015	0,999	0,84	3	0,87	3	0,75	2	48	8	6	5	5,2E-04	7,2E-05	1,7E-06
20	0,0018	0,9997	0,73	2	0,92	1	0,79	2	22	3	7	5	7,8E-04	3,8E-05	6,6E-06
21	0,0015	0,9997	-	4	0,89	2	0,73	1	9	6	4	3	5,9E-04	3,4E-05	4,8E-06
22	0,001	0,999	-	4	0,92	1	-	4	10	6	8	4	8,1E-04	8,0E-05	4,2E-06
23	0,001	0,9998	0,82	3	0,87	1	0,72	1	24	2	7	1	7,2E-03	4,7E-03	5,5E-05
24	0,001	0,999	0,80	2	0,80	2	-	4	6	4	8	1	6,6E-04	5,5E-05	2,6E-06
25	0,001	0,999	-	4	0,88	2	0,84	2	9	8	8	2	5,1E-04	0	8,0E-06

 

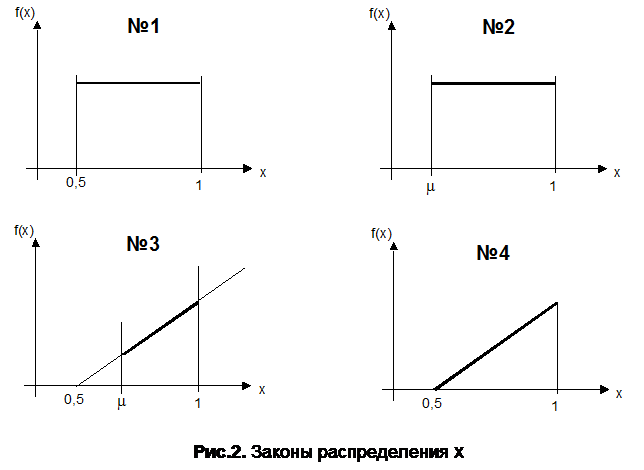Таблица 11

Таблица 12

Приложение 1

 

Таблица П1. F-распределение Фишера

Значения F

a n₁=1 n₁=2 n₁=3 n₁=4

n₂=10

0,05 4,96 4,10 3,71 3,48 0,10 10,04 7,56 6,55 5,99

n₂=11

0,05 4,84 3,98 3,59 3,26 0,10 9,65 7,2 6,22 5,67

n₂=12

0,05 4,75 3,88 3,36 3,41 0,10 9,33 7,2 5,67 5,74

n₂=13

0,05 4,67 3,8 3,49 3,18 0,10 9,07 6,7 6,22 5,2

n₂=14

0,05 4,60 3,74 3,34 3,11 0,10 8,86 6,51 5,56 5,03

 

 

Таблица П2. t- распределение Стьюдента

	Значения t
n	При a=0,1	При a=0,05
10	1,812	2,228
11	1,796	2,201
12	1,782	2,179
13	1,771	2,160
14	1,761	2,145

 

Приложение 2

Приложение 3

Оформление рабочего листа MS EXCEL в задаче 3

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

1

P1

P2

P3

P4

P5

P6

R

2

1

1

0

0

0

0

0

0

T1

T2

T3

T4

T5

T6

T7

T8

T9

3

2

9,33E-1

6,61E-02

7,86E-04

4,49E-04

2,49E-05

3,58E-05

1,87E-06

433

4

0,4

0,5

3

2

624

2,6

3,5

4

3

9,13E-1

8,39E-02

1,04E-03

1,12E-03

1,23E-04

7,14E-05

9,83E-06

12

13

21

23

34

45

52

26

62

67

72

5

4

9,07E-1

8,87E-02

1,11E-03

1,79E-03

2,85E-04

1,00E-04

2,17E-05

0,25

0,002

2,5

0,002

2

0,33

0,5

0,002

0,39

0,39

0,29

6

5

9,04E-1

8,99E-02

1,14E-03

2,41E-03

4,94E-04

1,22E-04

3,60E-05

7

6

9,03E-1

9,02E-02

1,14E-03

2,96E-03

7,34E-04

1,39E-04

5,14E-05

8

7

9,02E-1

9,03E-02

1,15E-03

3,44E-03

9,92E-04

1,52E-04

6,71E-05

9

8

9,01E-1

9,02E-02

1,14E-03

3,86E-03

1,26E-03

1,61E-04

8,26E-05

10

9

9,00E-1

9,02E-02

1,14E-03

4,23E-03

1,52E-03

1,68E-04

9,76E-05

11

10

8,99E-1

9,02E-02

1,14E-03

4,56E-03

1,78E-03

1,73E-04

1,12E-04

12

11

8,98E-1

9,01E-02

1,14E-03

4,84E-03

2,02E-03

1,77E-04

1,25E-04

…

…

…

…

…

…

…

…

…

34

33

8,92E-1

9,00E-02

1,13E-03

6,70E-03

4,34E-03

1,87E-04

2,41E-04

35

34

8,92E-1

9,00E-02

1,13E-03

6,71E-03

4,37E-03

1,87E-04

2,42E-04

36

35

8,92E-1

9,00E-02

1,13E-03

6,72E-03

4,39E-03

1,87E-04

2,43E-04

37

36

8,92E-1

9,00E-02

1,13E-03

6,73E-03

4,40E-03

1,87E-04

2,44E-04

38

37

8,92E-1

9,00E-02

1,13E-03

6,74E-03

4,42E-03

1,87E-04

2,45E-04

39

38

8,92E-1

9,00E-02

1,13E-03

6,75E-03

4,43E-03

1,87E-04

2,46E-04

40

39

8,92E-1

9,00E-02

1,13E-03

6,76E-03

4,45E-03

1,87E-04

2,47E-04

41

40

8,91E-1

9,00E-02

1,13E-03

6,76E-03

4,46E-03

1,87E-04

2,47E-04

42

41

8,91E-1

9,00E-02

1,13E-03

6,77E-03

4,47E-03

1,87E-04

2,48E-04

43

42

8,91E-1

9,00E-02

1,13E-03

6,77E-03

4,47E-03

1,87E-04

2,48E-04

44

43

8,91E-1

9,00E-02

1,13E-03

6,77E-03

4,48E-03

1,87E-04

2,49E-04

45

44

8,91E-1

9,00E-02

1,13E-03

6,78E-03

4,49E-03

1,87E-04

2,49E-04

46

45

8,91E-1

9,00E-02

1,13E-03

6,78E-03

4,49E-03

1,87E-04

2,49E-04

47

46

8,91E-01

9,00E-02

1,13E-03

6,78E-03

4,50E-03

1,87E-04

2,50E-04

48

47

8,91E-01

9,00E-02

1,13E-03

6,78E-03

4,50E-03

1,87E-04

2,50E-04

49

48

8,91E-01

9,00E-02

1,13E-03

6,79E-03

4,51E-03

1,87E-04

2,50E-04

50

49

8,91E-01

9,00E-02

1,13E-03

6,79E-03

4,51E-03

1,87E-04

2,50E-04

51

50

8,91E-01

9,00E-02

1,13E-03

6,79E-03

4,51E-03

1,87E-04

2,51E-04

52

51

8,91E-01

9,00E-02

1,13E-03

6,79E-03

4,51E-03

1,87E-04

2,51E-04

53

52

8,91E-01

9,00E-02

1,13E-03

6,79E-03

4,52E-03

1,87E-04

2,51E-04

Приложение 4

Оформление рабочего листа MS EXCEL в задаче 4

 

P6   P7

ОГЛАВЛЕНИЕ

Задача 1. Многофакторный регрессионный и корреляционный анализ... 3

Методические указания к решению задачи 1..................................... 6

Пример решения задачи 1.................................................................. 10

Литература к задаче 1......................................................................... 16

Задача 2. Динамическое программирование ............................................ 17

Методические указания к решению задачи 2................................... 18

Литература к задаче 2 ........................................................................ 20

Задача 3. Марковские случайные процессы ............................................. 20

Методические указания к решению задачи 3 .................................. 24

Литература к задаче 3 ........................................................................ 24

Задача 4. Метод Монте-Карло ................................................................... 25

Методические указания к решению задачи 4 .................................. 28

Последовательность решения задачи 4 .......................................... 30

Литература к задаче 4 ........................................................................ 31

Приложение 1 ............................................................................................. 32

Приложение 2 ............................................................................................. 32

Приложение 3 ............................................................................................. 35

Приложение 4 ............................................................................................. 37

 

 

МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ

 

 

Семестровое задание