Дисперсия обладает рядом математических свойств, использование которых значительно упрощает и облегчает её вычисление. Основные свойства дисперсии:

1. Дисперсия постоянной величины равна нулю.

2. Если все значения признака уменьшить или увеличить на какое-то постоянное число, то дисперсия от этого не изменится.

3. Если все значения признака уменьшить или увеличить в K раз, то дисперсия от этого соответственно увеличится или уменьшится в K² раз.

4. Сумма квадратов отклонений индивидуальных значений признака x от их средней 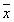меньше суммы квадратов отклонений индивидуальных значений признака от любого данного числа a при условии, что 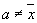, т.е.

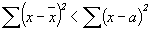
Доказано, что эти две суммы отличаются на квадрат разности между 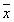и a

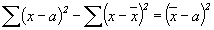
Это свойство дает возможность упрощать расчеты среднего квадратического отклонения путем замены громоздких отклонений от любого произвольно взятого числа, удобного для проведения расчетов, с последующей поправкой.

5. Дисперсия признака равна разности между средним квадратом значений признака и квадратом их средней, т.е.

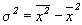
Рассмотрим вычисление дисперсий c применением её свойств.

Один из упрощенных способов вычисления дисперсии основан на следующем равенстве:

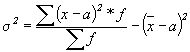
Этот способ исчисления дисперсии называется способом моментов или способом отсчета от условного нуля.

Дисперсия альтернативного признака. В ряде случаев возникает необходимость измерить вариацию альтернативного признака. Обозначив отсутствие интересующего признака через "0"; его наличие - через "1"; долю единиц, обладающих данным признаком - через q, исчислим среднее значение альтернативного признака и его дисперсию.

Среднее значение альтернативного признака равно

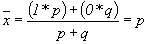
т.к. (сумма долей единиц, обладающих и не обладающих данным признаком, равна единице).

Дисперсия альтернативного признака определяется следующим образом:

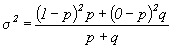
Подставив в формулу дисперсии вместо 1-p значение q=1-p, получим:

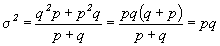
Таким образом, 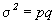, т.е. дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком, и доли единиц, им не обладающих.

Правило сложения дисперсий.

На вариацию признака влияют различные причины, факторы. Все они делятся на случайные и систематические (постоянные). Поэтому вариация может быть случайной, вызванной, вызванной действием случайных причин, и систематической, обусловленной воздействием постоянных факторов. В связи с этим возникает необходимость в определении случайной и систематической вариации, их роли в общей вариации и влияния на нее.

Как уже отмечалось, общая дисперсия характеризует общую вариацию признака под влиянием всех условий, всех причин, вызывающих эту вариацию, и рассчитывается следующим образом:

;

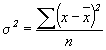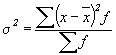
Для определения влияния постоянного фактора на величину вариации пользуются аналитической группировкой, т.е. расчленяют по нему всю совокупность на группы и определяют, как изменяется, варьируется общий результат под влиянием фактора, положенного в основание группировки.

Вариация, обусловленная фактором, положенным в основание группировки, называется межгрупповой вариацией.

Размеры ее определяются при помощи дисперсии групповых средних.

Межгрупповая дисперсия 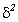характеризует колеблемость групповых или частных средних ( 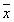_i) около общей средней (x_i) и исчисляется по формулам:

;

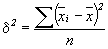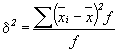
где x_i - средняя по каждой отдельной группе;

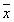- средняя по всей совокупности;

n - число единиц совокупности;

f - частоты или веса.

Таким образом, межгрупповая дисперсия (дисперсия групповых средних) равна средней арифметической из квадратов отклонений частных средних от общей средней.

Она характеризует систематическую вариацию, которая возникает под влиянием фактора признака, положенного в основу группировки.

Для определения влияния случайных факторов и их роли в общей вариации определяют дисперсию в пределах каждой группы, т.е. внутригрупповую дисперсию, а затем среднюю из внутригрупповых дисперсий.

Средняя из внутригрупповых дисперсий характеризует случайную вариацию, которая возникает по влиянием всех факторов, кроме положенного в основание группировки.

Чтобы определить её, надо рассчитать вначале внутригруппировочные дисперсии по каждой группе в отдельности, а затем среднюю их них.