Средняя арифметическая обладает некоторыми свойствами, которые определяют ее широкое применение в экономических расчетах и в практике статистического исследования.

Свойство 1. Средняя арифметическая постоянной величины равна этой постоянной:

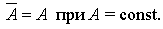
Свойство 2 (нулевое). Алгебраическая сумма линейных отклонений (разностей) индивидуальных значений признака от средней арифметической равна нулю:

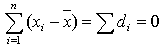для первичного ряда и 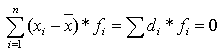для сгруппированных данных (d_i - линейные (индивидуальные) отклонения от средней, т.е. x_i - ).

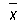Это свойство можно сформулировать следующим образом: сумма положительных отклонений от средней равна сумме отрицательных отклонений.

Логически оно означает, что все отклонения от средней в ту и в другую сторону, обусловленные случайными причинами, взаимно погашаются.

Свойство 3 (минимальное). Сумма квадратов отклонений индивидуальных значений признака от средней арифметической есть число минимальное:

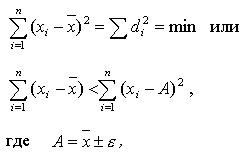
что означает: сумма квадратов отклонений индивидуальных значений признака каждой единицы совокупности от средней арифметической всегда меньше суммы квадратов отклонений вариантов признака от любого значения (А), сколь угодно мало отличающегося от средней у выбранной единицы исследуемой совокупности.

Для сгруппированных данных имеем:

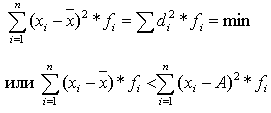
Минимальное и нулевое свойства средней арифметической применяются для проверки правильности расчета среднего уровня признака; при изучении закономерностей изменения уровней ряда динамики; для нахождения параметров уравнения регрессии при изучении корреляционной связи между признаками.

Рассмотренные свойства выражают сущностные черты средней арифметической. Существуют также расчетные (вычислительные) свойства средней арифметической, имеющие прикладное значение:

· если значения признака каждой единицы совокупности (все усредняемые варианты) уменьшить или увеличить на одну и ту же величину А, то и со средней арифметической произойдут аналогичные изменения;

· если значения признака каждой единицы совокупности разделить или умножить на какое-либо постоянное число А, то средняя арифметическая уменьшится или увеличится в А раз;

· если вес (частоту) каждого значения признака разделить на какое-либо постоянное число А, то средняя арифметическая не изменится.

В настоящее время вычислительные свойства средней арифметической потеряли свою актуальность в связи с использованием ЭВМ при расчете обобщающих статистических показателей.