Классическая электронная теория (разработана в 1900г. Друде, которую развил Лоренц) предполагает:
1) движение электронов подчиняется законам классической механики;
2) электроны друг с другом не взаимодействуют;
3) электроны взаимодействуют только с ионами кристаллической решетки, это взаимодействие сводится только к соударению;
4) в промежутках между соударениями электрон движется свободно;
5) электроны проводимости рассматривают как электронный газ, подобно идеальному газу; идеальный газ подчиняется закону равномерного распределения энергии по степеням свободы этому же закону подчиняется и электронный газ.
Классическая электронная теория хорошо объясняет существование сопротивления металлов, законы Ома и Джоуля-Ленца – зависимость электропроводимости от температуры и позволяют понять связь теплоты и электропроводимости металлов.
Однако в некоторых случаях классическая теория приводит к выводам находящихся в противореции с опытом, например, согласно этой теории удельное сопротивление с ростом температуры должно возрастать пропорционально корню из Т. Опыт подтверждает прямую пропорциональную зависимость 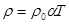 . В классической электронной теории теплоемкость металлов и явление сверхпроводимости совершенно не объяснимы.
. В классической электронной теории теплоемкость металлов и явление сверхпроводимости совершенно не объяснимы.
Трудности классической электронной теории связаны с тем, что:
а) электронная проводимость не подчиняется законам статики Максвелла-Больцмана;
б) не учитывается взаимодействие друг с другом;
в) не учитывается, что электрон движется в периодическом поле кристаллической решетки;
г) движение электронов описывается по законам классической механики, а не по законам квантовой механики.
На смену классической электронной теории пришла квантовая теория твердых тел, в которой преодолены трудности классической теории.
Необходимо отметить, что классическую электронную теорию применяют и сейчас, т.к. она проста и наглядна, а при малых концентрациях носителей заряда и больших температурах квантовая и классическая теории дают близкие результаты.
Качественное объяснение некоторых вопросов уже давалось в 8 кл. В 10 классе этим не ограничиваются, необходимо ввести важные для понимания материала формулы.
Следует обратить внимание учащихся на:
1) когда и зачем создана эта теория; 2) основные положения и модельные представления; 3) применение классической электронной теории (какие явления и факты объясняются данной теорией); 4) трудности классической электронной теории и причины их возникновения; 5) задачи классической ЭТ.
Электронная проводимость металла была доказана следующими фундаментальными опытами: Опыт Ринке: В точ. через проводник, состоящий из Cu-Al-Cu пропустили ток, за это время состав составной проводник прошел огромный заряд 3,5 106Кл, следовательно переноса вещества не наблюдалось, масса осталась неизменной, соприкасающиеся поверхности не изменились. Вывод – перенос заряда в металлах осуществляется частицами, входящими в состав всех металлов (электроны).
Предлагается школьникам задача: какое изменение произойдет если бы ток представлял собой движение ионов?
В опытах Мандельштама и Папалекси, Стюарта, Толмена лежала следующая идея – регистрация инерционного движения электронов.
Закон Ома для участка цепи выводится на основе опыта.
Скорость распространения электрического тока в проводниках – это скорость с которой распространяется действие электрического поля на заряды в проводнике. Поле почти мгновенно увлекает электроны в упорядоченное и очень медленное движение доли мм/сек.
В 10 классе показывают, что средняя скорость упорядоченного движения электронов под действием электрического поля определяет силу тока в проводнике.
Пусть проводник имеет поперечное сечение площадью S, за положительное направление принимают движение слева на право.
Обозначим заряд каждой частицы через q0. Общий заряд, проходящий через поперечное сечение равно: 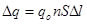 .
.
Если частица движется слева на право со средней скоростью V, то за время дельта t все чстицы, заключающеся в рассмотрении объема пройдут через поперечное сечение. 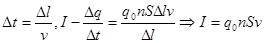 .
.
Закон Ома для полной цепи.
Любая замкнутая электрическая цепь состоит из внешних и внутренних участков, и внешних и внутренних сопротивлений.
Для поддержания в цепи электрического тока в течение длительного времени необходим источник, внутри которого непрерывно происходило бы разделение электрических зарядов. В результате чего между полюсами источников поддерживалась бы разность потенциалов.
ЭДС называют скалярную физическую величину, являющуюся энергетической характеристикой источника тока.
ЭДС равна отношению работы, совершаемой сторонними силами при перемещении электрического заряда по замкнутой цепи к этому заряду. E=Aст/q.
Силы в результате действия которых в источнике ток происходят разделения зарядов, принято называть сторонними.
При выводе закона Ома для замкнутой цепи можно использовать различные методические подходы:
1) при перемещении по цепи заряда q сторонние силы в источнике совершают работу A=qE. При движении заряда на внешнем участке цепи преобразуется энергия стационарного поля, созданного и поддерживаемого источником Aвнеш=qU, U - напряженность на внешнем участке. На внутреннем A2=qUвн.
A=A1+A2, qE=qU+qUвн, E=U+Uвн, U=IR, Uвн=Ir, E=Ir+Ir=I(R+r) или I=E/(R+r)
Таким образом сила тока в цепи равна отношению Еист к сумме сопротивлений цепи.
2) Рассматривается та же цепь. За время дельта t через поперечное сечение проводника пройдет электрический заряд дельта q. Работа сторонних сил по перемещению заряда Аст=Еq=EIt.
При совершении этой работы на внутренних и внешних участках цепи, сопротивление которых r и R выделяется некоторое количество теплоты 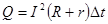 , согласно закону сохранения энергии Аст=Q, следовательно I=E/(R+r). При R стремящимся к нулю, получается короткое замыкание, т.к. r мало.
, согласно закону сохранения энергии Аст=Q, следовательно I=E/(R+r). При R стремящимся к нулю, получается короткое замыкание, т.к. r мало.
Здесь изучается последовательное и параллельное соединение потребителей: U=U1+U2, Rоб=R1+R2. При параллельном соединении I=I1+I2, 1/Rоб=1/R1+1/R2.
В конце изучается работа и мощность тока, закон Джоуля-Ленца – количество теплоты, выделяемое при прохождении электрического тока по проводнику пропорционально квадрату силы тока, сопротивлению и времени прохождения тока через проводник: 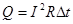 .
.
Дата: 2019-05-28, просмотров: 315.